高斯混合模型橢球?
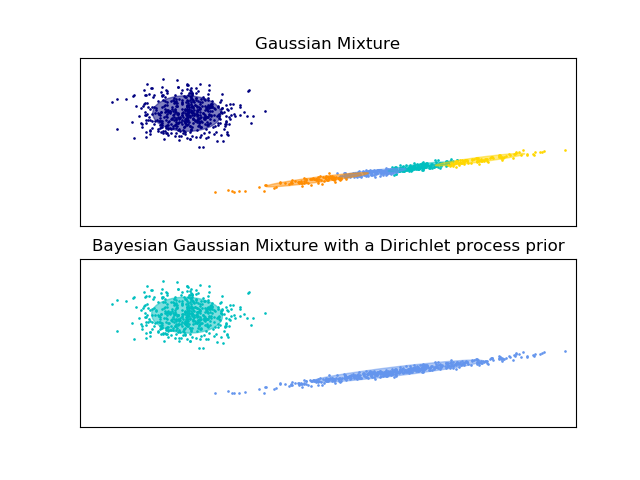
繪制兩個高斯混合模型的置信橢球, 使用的是最大期望算法 (GaussianMixture 類) 和變分推理(具有Dirichlet過程先驗的BayesianGaussianMixture類模型)。
這兩個模型都可以使用五個成分來擬合數據。請注意,期望最大化模型必須使用所有五個成分,而變分推理模型將只有效地使用一個良好的擬合所需的數量。在這里,我們可以看到期望最大化模型任意地分割一些成分,因為它試圖擬合太多的部分,而Dirichlet過程模型則自動調整它的狀態數量。
這個例子沒有顯示出來,因為我們所處的是一個低維空間,但是Dirichlet過程模型的另一個優點是,它可以有效地擬合完全協方差矩陣,即使每個聚類中的樣本數少于數據中的維數,這是由于推理算法的正則化特性。
import itertools
import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn import mixture
color_iter = itertools.cycle(['navy', 'c', 'cornflowerblue', 'gold',
'darkorange'])
def plot_results(X, Y_, means, covariances, index, title):
splot = plt.subplot(2, 1, 1 + index)
for i, (mean, covar, color) in enumerate(zip(
means, covariances, color_iter)):
v, w = linalg.eigh(covar)
v = 2. * np.sqrt(2.) * np.sqrt(v)
u = w[0] / linalg.norm(w[0])
# as the DP will not use every component it has access to
# unless it needs it, we shouldn't plot the redundant
# components.
if not np.any(Y_ == i):
continue
plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], .8, color=color)
# Plot an ellipse to show the Gaussian component
angle = np.arctan(u[1] / u[0])
angle = 180. * angle / np.pi # convert to degrees
ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
ell.set_clip_box(splot.bbox)
ell.set_alpha(0.5)
splot.add_artist(ell)
plt.xlim(-9., 5.)
plt.ylim(-3., 6.)
plt.xticks(())
plt.yticks(())
plt.title(title)
# Number of samples per component
n_samples = 500
# Generate random sample, two components
np.random.seed(0)
C = np.array([[0., -0.1], [1.7, .4]])
X = np.r_[np.dot(np.random.randn(n_samples, 2), C),
.7 * np.random.randn(n_samples, 2) + np.array([-6, 3])]
# Fit a Gaussian mixture with EM using five components
gmm = mixture.GaussianMixture(n_components=5, covariance_type='full').fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, 0,
'Gaussian Mixture')
# Fit a Dirichlet process Gaussian mixture using five components
dpgmm = mixture.BayesianGaussianMixture(n_components=5,
covariance_type='full').fit(X)
plot_results(X, dpgmm.predict(X), dpgmm.means_, dpgmm.covariances_, 1,
'Bayesian Gaussian Mixture with a Dirichlet process prior')
plt.show()
腳本的總運行時間:(0分0.188秒)
