L1-Logistic回歸的正則化路徑?
基于iris數據集的二分類問題訓練 L1-懲罰 Logistic回歸模型。
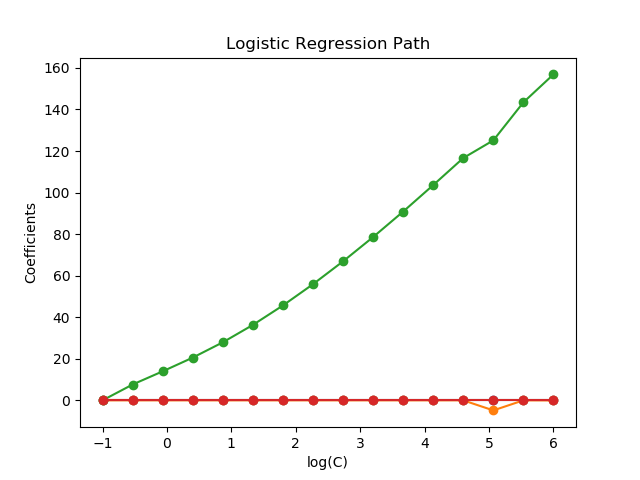
模型由強正則化到最少正則化。模型的4個系數被收集并繪制成“正則化路徑”:在圖的左邊(強正則化者),所有系數都精確地為0。當正則化逐步放松時,系數可以一個接一個地得到非零值。
在這里,我們選擇了線性求解器,因為它可以有效地優化非光滑的、稀疏的帶l1懲罰的Logistic回歸損失。
還請注意,我們為公差設置了一個較低的值,以確保模型在收集系數之前已經收斂。
Computing regularization path ...
This took 0.072s
print(__doc__)
# Author: Alexandre Gramfort <alexandre.gramfort@inria.fr>
# License: BSD 3 clause
from time import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn import datasets
from sklearn.svm import l1_min_c
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y != 2]
y = y[y != 2]
X /= X.max() # Normalize X to speed-up convergence
# #############################################################################
# Demo path functions
cs = l1_min_c(X, y, loss='log') * np.logspace(0, 7, 16)
print("Computing regularization path ...")
start = time()
clf = linear_model.LogisticRegression(penalty='l1', solver='liblinear',
tol=1e-6, max_iter=int(1e6),
warm_start=True,
intercept_scaling=10000.)
coefs_ = []
for c in cs:
clf.set_params(C=c)
clf.fit(X, y)
coefs_.append(clf.coef_.ravel().copy())
print("This took %0.3fs" % (time() - start))
coefs_ = np.array(coefs_)
plt.plot(np.log10(cs), coefs_, marker='o')
ymin, ymax = plt.ylim()
plt.xlabel('log(C)')
plt.ylabel('Coefficients')
plt.title('Logistic Regression Path')
plt.axis('tight')
plt.show()
腳本的總運行時間:(0分0.151秒)
