強異常數據集上的Huber回歸與嶺回歸?
在有異常值的數據集上擬合嶺回歸和Huber回歸。
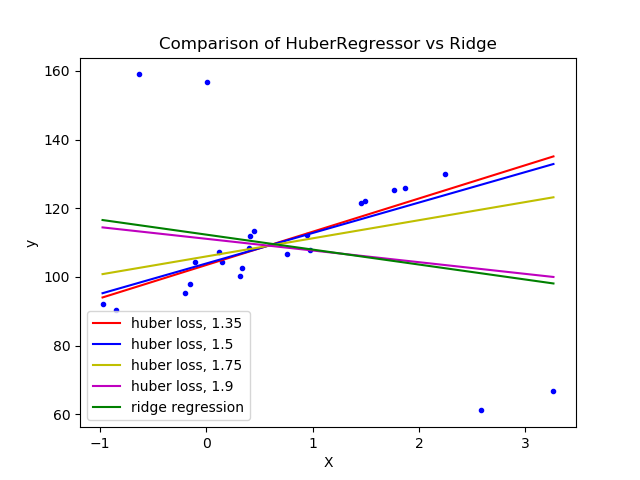
這個例子表明, 嶺回歸的預測受數據集的離群值的影響很大。Huber回歸受離群值的影響較小, 因為模型用的線性損失。隨著Huber回歸方程參數epsilon的增大,決策函數接近于嶺回歸。
# Authors: Manoj Kumar mks542@nyu.edu
# License: BSD 3 clause
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.linear_model import HuberRegressor, Ridge
# Generate toy data.
rng = np.random.RandomState(0)
X, y = make_regression(n_samples=20, n_features=1, random_state=0, noise=4.0,
bias=100.0)
# Add four strong outliers to the dataset.
X_outliers = rng.normal(0, 0.5, size=(4, 1))
y_outliers = rng.normal(0, 2.0, size=4)
X_outliers[:2, :] += X.max() + X.mean() / 4.
X_outliers[2:, :] += X.min() - X.mean() / 4.
y_outliers[:2] += y.min() - y.mean() / 4.
y_outliers[2:] += y.max() + y.mean() / 4.
X = np.vstack((X, X_outliers))
y = np.concatenate((y, y_outliers))
plt.plot(X, y, 'b.')
# Fit the huber regressor over a series of epsilon values.
colors = ['r-', 'b-', 'y-', 'm-']
x = np.linspace(X.min(), X.max(), 7)
epsilon_values = [1.35, 1.5, 1.75, 1.9]
for k, epsilon in enumerate(epsilon_values):
huber = HuberRegressor(alpha=0.0, epsilon=epsilon)
huber.fit(X, y)
coef_ = huber.coef_ * x + huber.intercept_
plt.plot(x, coef_, colors[k], label="huber loss, %s" % epsilon)
# Fit a ridge regressor to compare it to huber regressor.
ridge = Ridge(alpha=0.0, random_state=0, normalize=True)
ridge.fit(X, y)
coef_ridge = ridge.coef_
coef_ = ridge.coef_ * x + ridge.intercept_
plt.plot(x, coef_, 'g-', label="ridge regression")
plt.title("Comparison of HuberRegressor vs Ridge")
plt.xlabel("X")
plt.ylabel("y")
plt.legend(loc=0)
plt.show()
腳本的總運行時間:(0分0.118秒)
