魯棒線性估計擬合?
這里,正弦函數與3階多項式擬合,其數值接近于零。
在不同的情況下,穩健的擬合會被降級:
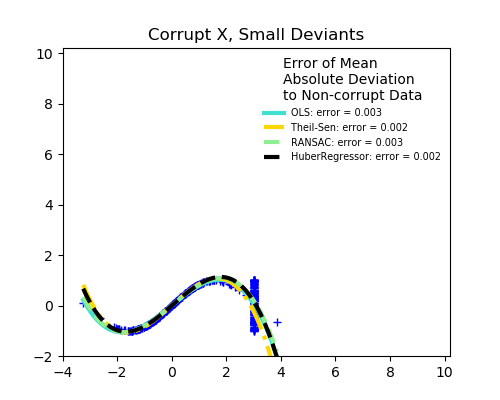
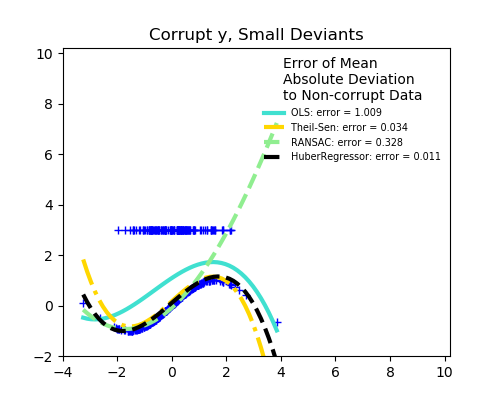
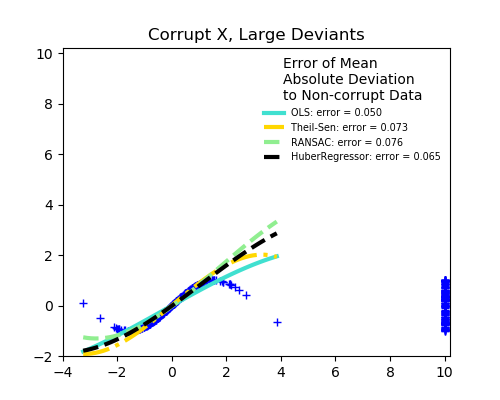
沒有測量誤差,只有建模誤差(用多項式擬合正弦) X測量誤差 y測量誤差
對非損壞新數據的中位絕對偏差用來判斷預測的質量。
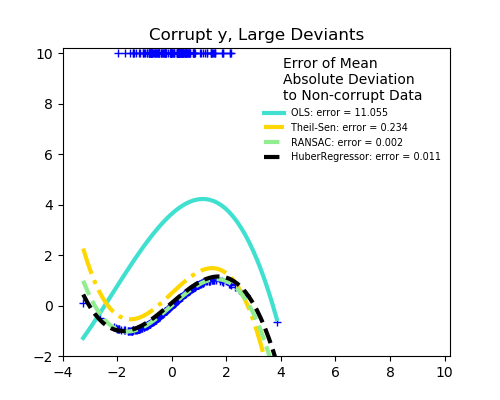
我們能看到的是:
RANSAC對y方向的強離群值是有利的。 TheilSen對X方向和y方向的小離群值都很好,但是有一個斷點,它的表現比OLS差。 HuberRegressor的分數不能直接與TheilSen和RANSAC進行比較,因為它并不試圖完全過濾異常值,而是減少了它們的影響。 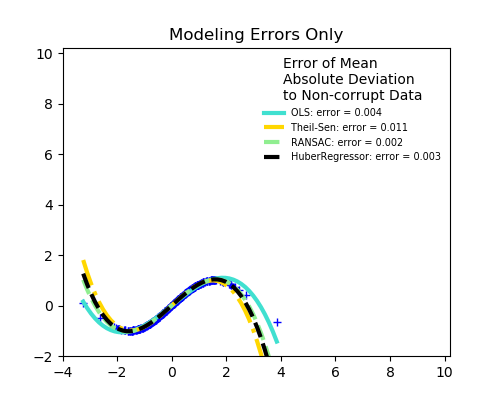
from matplotlib import pyplot as plt
import numpy as np
from sklearn.linear_model import (
LinearRegression, TheilSenRegressor, RANSACRegressor, HuberRegressor)
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
np.random.seed(42)
X = np.random.normal(size=400)
y = np.sin(X)
# Make sure that it X is 2D
X = X[:, np.newaxis]
X_test = np.random.normal(size=200)
y_test = np.sin(X_test)
X_test = X_test[:, np.newaxis]
y_errors = y.copy()
y_errors[::3] = 3
X_errors = X.copy()
X_errors[::3] = 3
y_errors_large = y.copy()
y_errors_large[::3] = 10
X_errors_large = X.copy()
X_errors_large[::3] = 10
estimators = [('OLS', LinearRegression()),
('Theil-Sen', TheilSenRegressor(random_state=42)),
('RANSAC', RANSACRegressor(random_state=42)),
('HuberRegressor', HuberRegressor())]
colors = {'OLS': 'turquoise', 'Theil-Sen': 'gold', 'RANSAC': 'lightgreen', 'HuberRegressor': 'black'}
linestyle = {'OLS': '-', 'Theil-Sen': '-.', 'RANSAC': '--', 'HuberRegressor': '--'}
lw = 3
x_plot = np.linspace(X.min(), X.max())
for title, this_X, this_y in [
('Modeling Errors Only', X, y),
('Corrupt X, Small Deviants', X_errors, y),
('Corrupt y, Small Deviants', X, y_errors),
('Corrupt X, Large Deviants', X_errors_large, y),
('Corrupt y, Large Deviants', X, y_errors_large)]:
plt.figure(figsize=(5, 4))
plt.plot(this_X[:, 0], this_y, 'b+')
for name, estimator in estimators:
model = make_pipeline(PolynomialFeatures(3), estimator)
model.fit(this_X, this_y)
mse = mean_squared_error(model.predict(X_test), y_test)
y_plot = model.predict(x_plot[:, np.newaxis])
plt.plot(x_plot, y_plot, color=colors[name], linestyle=linestyle[name],
linewidth=lw, label='%s: error = %.3f' % (name, mse))
legend_title = 'Error of Mean\nAbsolute Deviation\nto Non-corrupt Data'
legend = plt.legend(loc='upper right', frameon=False, title=legend_title,
prop=dict(size='x-small'))
plt.xlim(-4, 10.2)
plt.ylim(-2, 10.2)
plt.title(title)
plt.show()
腳本的總運行時間:(0分2.564秒)
