在回歸模型中轉換目標的效果?

在此示例中，我們概述了sklearn.compose.TransformedTargetRegressor。兩個示例說明了在學習線性回歸模型之前轉換目標的好處。第一個示例使用合成數據，而第二個示例基于Boston住房數據集。

# 作者: Guillaume Lemaitre <guillaume.lemaitre@inria.fr>
# 執照: BSD 3 clause


import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from distutils.version import LooseVersion

print(__doc__)

綜合實例

from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import RidgeCV
from sklearn.compose import TransformedTargetRegressor
from sklearn.metrics import median_absolute_error, r2_score


# `normed` is being deprecated in favor of `density` in histograms
if LooseVersion(matplotlib.__version__) >= '2.1':
    density_param = {'density': True}
else:
    density_param = {'normed': True}

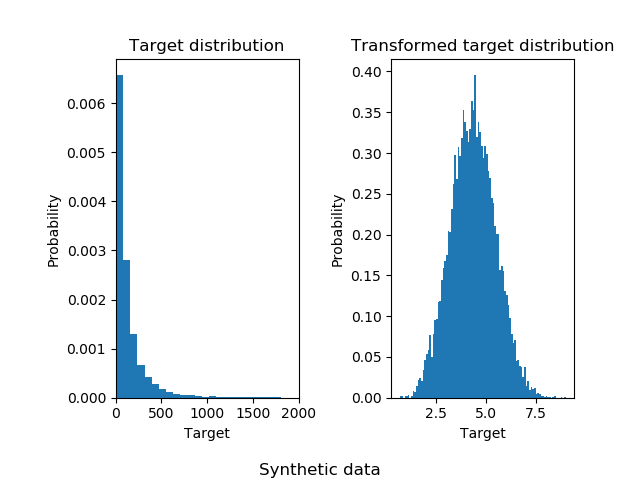
生成了一個綜合隨機回歸問題。通過以下方式修改目標y：（i）轉換所有目標，使所有條目均為非負數；（ii）應用指數函數以獲得無法使用簡單線性模型擬合的非線性目標。

因此，在訓練線性回歸模型并將其用于預測之前，將使用對數（np.log1p）和指數函數（np.expm1）轉換目標。

X, y = make_regression(n_samples=10000, noise=100, random_state=0)
y = np.exp((y + abs(y.min())) / 200)
y_trans = np.log1p(y)

下面說明在應用對數函數之前和之后目標的概率密度函數。

f, (ax0, ax1) = plt.subplots(1, 2)

ax0.hist(y, bins=100, **density_param)
ax0.set_xlim([0, 2000])
ax0.set_ylabel('Probability')
ax0.set_xlabel('Target')
ax0.set_title('Target distribution')

ax1.hist(y_trans, bins=100, **density_param)
ax1.set_ylabel('Probability')
ax1.set_xlabel('Target')
ax1.set_title('Transformed target distribution')

f.suptitle("Synthetic data", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

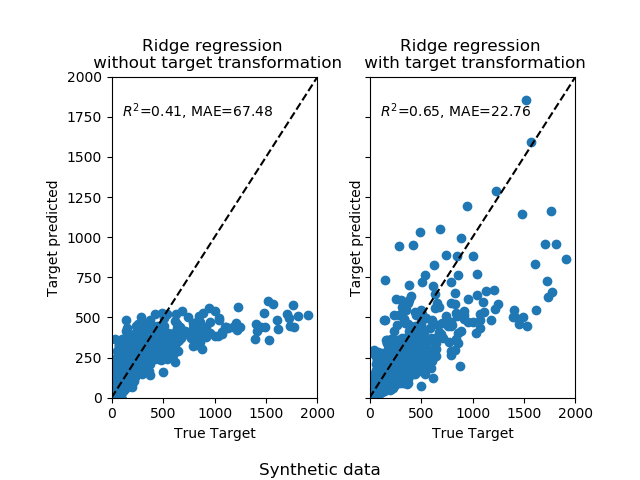
首先，將線性模型應用于原始目標。由于非線性，訓練的模型在預測期間將不精確。隨后，使用對數函數將目標線性化，即使使用中位數絕對誤差（MAE）報告的相似線性模型，也可以實現更好的預測。

f, (ax0, ax1) = plt.subplots(1, 2, sharey=True)

regr = RidgeCV()
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)

ax0.scatter(y_test, y_pred)
ax0.plot([0, 2000], [0, 2000], '--k')
ax0.set_ylabel('Target predicted')
ax0.set_xlabel('True Target')
ax0.set_title('Ridge regression \n without target transformation')
ax0.text(100, 1750, r'$R^2$=%.2f, MAE=%.2f' % (
    r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax0.set_xlim([0, 2000])
ax0.set_ylim([0, 2000])

regr_trans = TransformedTargetRegressor(regressor=RidgeCV(),
                                        func=np.log1p,
                                        inverse_func=np.expm1)
regr_trans.fit(X_train, y_train)
y_pred = regr_trans.predict(X_test)

ax1.scatter(y_test, y_pred)
ax1.plot([0, 2000], [0, 2000], '--k')
ax1.set_ylabel('Target predicted')
ax1.set_xlabel('True Target')
ax1.set_title('Ridge regression \n with target transformation')
ax1.text(100, 1750, r'$R^2$=%.2f, MAE=%.2f' % (
    r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax1.set_xlim([0, 2000])
ax1.set_ylim([0, 2000])

f.suptitle("Synthetic data", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])

實際數據集

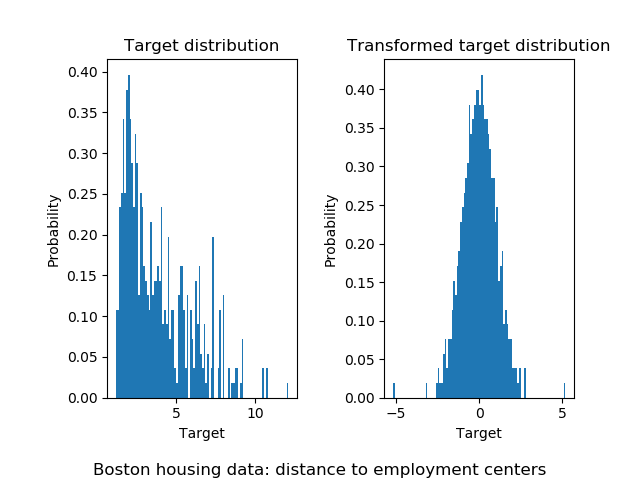
以類似的方式，波士頓住房數據集用于顯示學習模型之前變換目標的影響。在此示例中，要預測的目標對應于到五個波士頓就業中心的加權距離。

from sklearn.datasets import load_boston
from sklearn.preprocessing import QuantileTransformer, quantile_transform

dataset = load_boston()
target = np.array(dataset.feature_names) == "DIS"
X = dataset.data[:, np.logical_not(target)]
y = dataset.data[:, target].squeeze()
y_trans = quantile_transform(dataset.data[:, target],
                             n_quantiles=300,
                             output_distribution='normal',
                             copy=True).squeeze()

使用sklearn.preprocessing.QuantileTransformer，以便在應用sklearn.linear_model.RidgeCV模型之前，目標遵循正態分布。

f, (ax0, ax1) = plt.subplots(1, 2)

ax0.hist(y, bins=100, **density_param)
ax0.set_ylabel('Probability')
ax0.set_xlabel('Target')
ax0.set_title('Target distribution')

ax1.hist(y_trans, bins=100, **density_param)
ax1.set_ylabel('Probability')
ax1.set_xlabel('Target')
ax1.set_title('Transformed target distribution')

f.suptitle("Boston housing data: distance to employment centers", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)

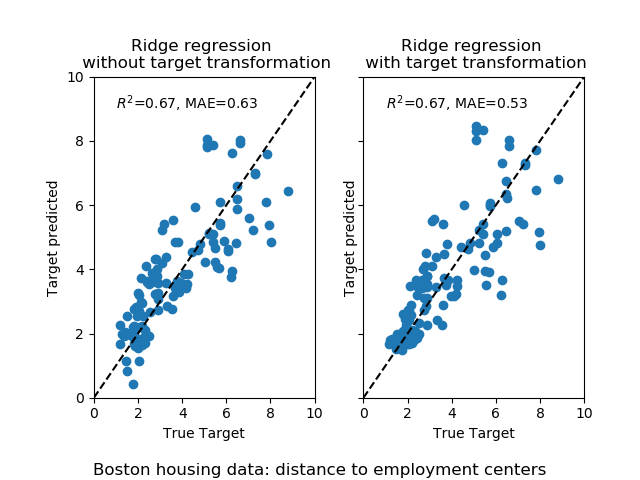
轉換器的影響要弱于綜合數據。但是，該變換引起MAE的降低。

f, (ax0, ax1) = plt.subplots(1, 2, sharey=True)

regr = RidgeCV()
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)

ax0.scatter(y_test, y_pred)
ax0.plot([0, 10], [0, 10], '--k')
ax0.set_ylabel('Target predicted')
ax0.set_xlabel('True Target')
ax0.set_title('Ridge regression \n without target transformation')
ax0.text(1, 9, r'$R^2$=%.2f, MAE=%.2f' % (
    r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax0.set_xlim([0, 10])
ax0.set_ylim([0, 10])

regr_trans = TransformedTargetRegressor(
    regressor=RidgeCV(),
    transformer=QuantileTransformer(n_quantiles=300,
                                    output_distribution='normal'))
regr_trans.fit(X_train, y_train)
y_pred = regr_trans.predict(X_test)

ax1.scatter(y_test, y_pred)
ax1.plot([0, 10], [0, 10], '--k')
ax1.set_ylabel('Target predicted')
ax1.set_xlabel('True Target')
ax1.set_title('Ridge regression \n with target transformation')
ax1.text(1, 9, r'$R^2$=%.2f, MAE=%.2f' % (
    r2_score(y_test, y_pred), median_absolute_error(y_test, y_pred)))
ax1.set_xlim([0, 10])
ax1.set_ylim([0, 10])

f.suptitle("Boston housing data: distance to employment centers", y=0.035)
f.tight_layout(rect=[0.05, 0.05, 0.95, 0.95])

plt.show()

腳本的總運行時間：（0分鐘1.447秒）