使用KBinsDiscretizer離散化連續特征?

該示例比較了帶有或不帶有離散化實值特征的線性回歸（線性模型）和決策樹（基于樹的模型）的預測結果。

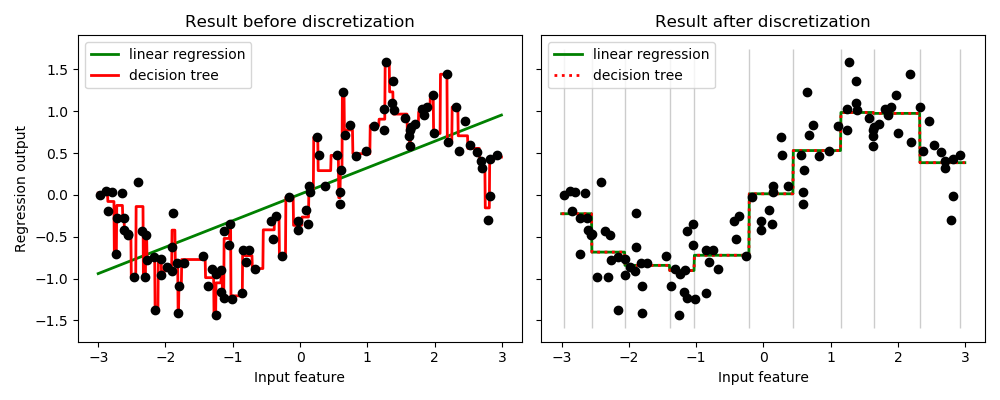
如離散化之前的結果所示，線性模型的建立速度很快，解釋起來也相對簡單，但是只能建模線性關系，而決策樹則可以構建更為復雜的數據模型。使線性模型在連續數據上更強大的一種方法是使用離散化（也稱為分箱）。在示例中，我們離散化了特征，并對轉換后的數據進行了一次熱編碼。請注意，如果分箱的寬度不太合理，則過擬合的風險似乎會大大增加，因此通常應在交叉驗證下調整離散器參數。

離散化之后，線性回歸和決策樹做出完全相同的預測。由于每個分箱倉中的要素都是恒定的，因此任何模型都必須為倉中的所有點預測相同的值。與離散化之前的結果相比，線性模型變得更加靈活，而決策樹的靈活性則大大降低。請注意，合并功能通常不會對基于樹的模型產生任何有益影響，因為這些模型可以學習將數據拆分到任何地方。

# 作者: Andreas Müller
#         Hanmin Qin <qinhanmin2005@sina.com>
# 執照: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeRegressor

print(__doc__)

# 構建數據集
rnd = np.random.RandomState(42)
X = rnd.uniform(-3, 3, size=100)
y = np.sin(X) + rnd.normal(size=len(X)) / 3
X = X.reshape(-1, 1)

# 用KBinsDiscretizer轉換數據集
enc = KBinsDiscretizer(n_bins=10, encode='onehot')
X_binned = enc.fit_transform(X)

# 用原始數據集進行預測
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True, figsize=(10, 4))
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)
reg = LinearRegression().fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color='green',
         label="linear regression")
reg = DecisionTreeRegressor(min_samples_split=3, random_state=0).fit(X, y)
ax1.plot(line, reg.predict(line), linewidth=2, color='red',
         label="decision tree")
ax1.plot(X[:, 0], y, 'o', c='k')
ax1.legend(loc="best")
ax1.set_ylabel("Regression output")
ax1.set_xlabel("Input feature")
ax1.set_title("Result before discretization")

# 用轉換后的數據進行預測
line_binned = enc.transform(line)
reg = LinearRegression().fit(X_binned, y)
ax2.plot(line, reg.predict(line_binned), linewidth=2, color='green',
         linestyle='-', label='linear regression')
reg = DecisionTreeRegressor(min_samples_split=3,
                            random_state=0).fit(X_binned, y)
ax2.plot(line, reg.predict(line_binned), linewidth=2, color='red',
         linestyle=':', label='decision tree')
ax2.plot(X[:, 0], y, 'o', c='k')
ax2.vlines(enc.bin_edges_[0], *plt.gca().get_ylim(), linewidth=1, alpha=.2)
ax2.legend(loc="best")
ax2.set_xlabel("Input feature")
ax2.set_title("Result after discretization")

plt.tight_layout()
plt.show()

輸出：

腳本的總運行時間：（0分鐘0.203秒）