支持向量機：不均衡數據集的分割超平面?

對于樣本不均衡的數據，使用SVC查找最佳分割超平面。

我們首先找到普通SVC的分割平面，然后用虛銜繪制對不平衡的樣本類進行自動校正的分割平面。

注意：通過將SVC（kernel =“ linear”）替換為SGDClassifier（loss =“ hinge”），這個案例中的代碼也可以跑通。將SGDClassifier的損失函數設置為hinge將產生類似線性核的SVC的行為。

例如，嘗試代替SVC：

clf = SGDClassifier(n_iter=100, alpha=0.01)

輸出：

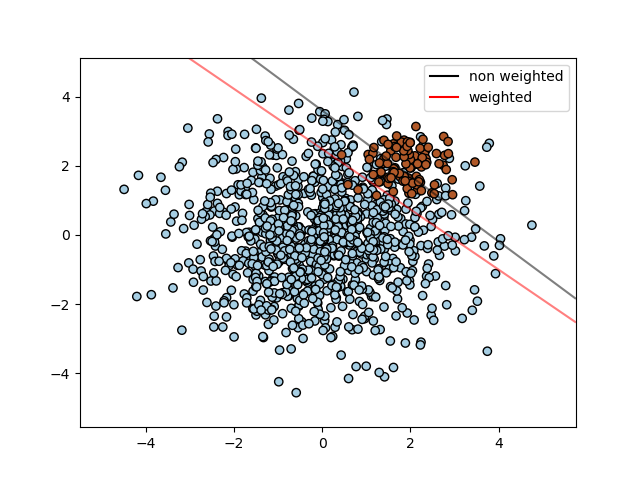
輸入：

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs

# 創造兩簇隨機的點
n_samples_1 = 1000
n_samples_2 = 100
centers = [[0.0, 0.0], [2.0, 2.0]]
clusters_std = [1.5, 0.5]
X, y = make_blobs(n_samples=[n_samples_1, n_samples_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False)

# 擬合模型并得到分割超平面
clf = svm.SVC(kernel='linear', C=1.0)
clf.fit(X, y)

# 擬合模型并得到處理了樣本不平衡的分割超平面
wclf = svm.SVC(kernel='linear', class_weight={1: 10})
wclf.fit(X, y)

# 繪制樣本
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors='k')

# 為兩個分類器繪制決策邊界
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

# 創造網格來評估模型
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T

# 繪制分割的超平面
Z = clf.decision_function(xy).reshape(XX.shape)

# 繪制決策邊界和邊際
a = ax.contour(XX, YY, Z, colors='k', levels=[0], alpha=0.5, linestyles=['-'])

# 繪制做了樣本平衡后的分割的超平面
Z = wclf.decision_function(xy).reshape(XX.shape)

# 繪制做了樣本平衡后的決策邊界和邊際
b = ax.contour(XX, YY, Z, colors='r', levels=[0], alpha=0.5, linestyles=['-'])

plt.legend([a.collections[0], b.collections[0]], ["non weighted", "weighted"],
           loc="upper right")
plt.show()

腳本的總運行時間：（0分鐘0.144秒）