RBF核支持向量機的參數?
本案例展示了參數gamma和C對徑向基函數核函數(RBF)下的支持向量機的影響。
直觀地說,gamma參數定義了“單個訓練樣本對整個模型的影響程度”,gamma值很低表示“影響深遠”,gamma值高卻表示“影響不大”。gamma參數可以看作是模型選出的那些支持向量的影響半徑的倒數。
C參數在“訓練樣本的正確分類”與“決策編輯最大化”之間做出權衡。對于較大的C值,如果模型的決策函數本身可以更好地正確分類所有訓練點,則可以接受較小的邊際。較低的C將鼓勵更大的邊際,因此會簡化決策功能,降低訓練的準確性。換句話說,C在SVM中充當正則化參數。
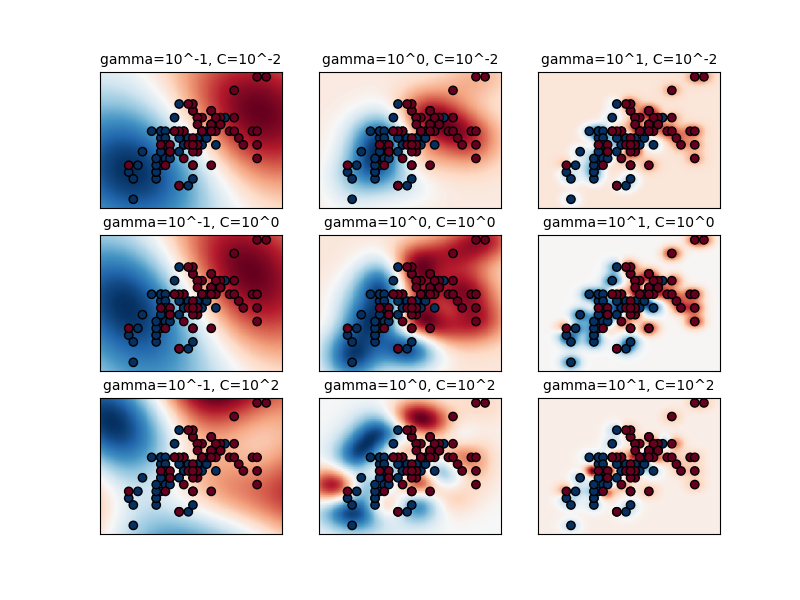
第一張圖是一個簡單分類問題的決策函數的可視化,這個決策函數被給定了一系列的參數值,且該分類問題僅僅涉及2個特征和2個可能的目標類別(二分類)。請注意,對于具有更多特征或目標類別的問題,類似的圖像是無法繪制的。
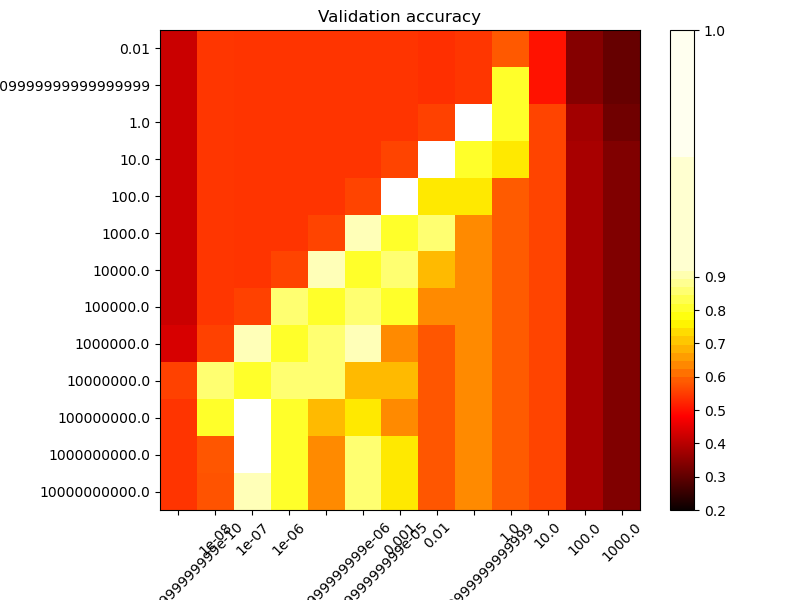
第二幅圖是一個熱力圖,該圖中分類器的交叉驗證準確率是參數C和gamma的函數(譯者注:即顏色深淺代表準確率,橫縱坐標是C和gamma)。在此案例中,為了說明我們的目的,我們探索了一個相對較大的網格。實際上,從到的對數網格通常就足夠了。如果最佳參數位于網格的邊界上,則可以在后續搜索中沿該方向擴展。
請注意,熱力圖具有特殊的顏色條,顏色條的中點上的數值接近性能最佳的模型的得分值,依賴于這張圖我們可以在眨眼之間就能輕松分辨模型的優劣。
(譯者注:一種典型的顏色條是 深色-淺色-深色 的顏色結構,本文中"顏色條的中點"是指淺色的部分。我們可以通過代碼來調整顏色條的顏色結構,使顯眼的顏色與我們希望捕獲的模型結果匹配。本案例中將淺色的部分與最佳模型得分匹配,這樣就可以一眼在熱力圖中看出顯眼的淺色部分所代表的最佳模型。)
模型的行為對gamma參數非常敏感。如果gamma太大,則支持向量的影響區域的半徑就只能包括支持向量本身,這種情況下,使用C進行的正則化也無法防止過擬合。
當gamma非常小時,該模型太受約束,無法捕獲數據的復雜性或“形狀”。任何選定的支持向量的影響區域都會包括整個訓練集。所得模型的行為將類似于帶有一組超平面的線性模型,該超平面分割任意兩個類別不同的數據點的高密度中心。
對于不大也不小、處于中間的gamma值,如第二張圖所示,我們可以在C和gamma的對角線上找到好的模型。通過增加正確分類每個點的重要性(設置較大的C值),可以提高平滑模型(較小的gamma值)的復雜度,所以對角線上能夠獲得提高了性能的良好的模型。
最后,我們還可以觀察到,對于某些不大不小的gamma值,當C變得非常大時,我們得到的模型性能一致:此時,通過強制追求更大的邊際來進行正則化就沒有必要了。RBF核函數的半徑就可以充當良好的結構調整器。不過在實踐中,更有趣的事情依然是:用較低的C值簡化決策函數,以便支持使用較少內存且預測速度更快的模型。
我們還應注意,分數的微小差異是由交叉驗證過程的隨機分裂造成的。可以通過增加CV迭代次數n_splits來消除那些虛假的變化,但這會浪費計算時間。增加C_range和gamma_range步驟的值數量將增加超參數熱力圖的分辨率。
輸出:
輸出:
The best parameters are {'C': 1.0, 'gamma': 0.1} with a score of 0.97
輸入:
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import Normalize
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import GridSearchCV
# 一個很實用的函數,可將顏色圖的中點移動到感興趣的值附近。
class MidpointNormalize(Normalize):
def __init__(self, vmin=None, vmax=None, midpoint=None, clip=False):
self.midpoint = midpoint
Normalize.__init__(self, vmin, vmax, clip)
def __call__(self, value, clip=None):
x, y = [self.vmin, self.midpoint, self.vmax], [0, 0.5, 1]
return np.ma.masked_array(np.interp(value, x, y))
# #############################################################################
# 導入并準備數據集
#
# 為網格搜索準備數據集
iris = load_iris()
X = iris.data
y = iris.target
# 用于決策功能可視化的數據集:我們僅將前兩個特征保留在X中,并對數據集進行子采樣,以僅保留2個類,并使其成為二分類問題。
X_2d = X[:, :2]
X_2d = X_2d[y > 0]
y_2d = y[y > 0]
y_2d -= 1
# 縮放數據以進行SVM訓練通常是一個好主意。在此示例中,我們在縮放數據時有點"作弊",我們縮放了全部數據,而不是將轉換器在訓練集上擬合,然后縮放到測試集上。
scaler = StandardScaler()
X = scaler.fit_transform(X)
X_2d = scaler.fit_transform(X_2d)
# #############################################################################
# 訓練分類器
#
# 對于初始搜索,以10為底的對數網格通常會很有幫助。使用2為基數,可以實現更精細的調整,但就算成本要高得多。
C_range = np.logspace(-2, 10, 13)
gamma_range = np.logspace(-9, 3, 13)
param_grid = dict(gamma=gamma_range, C=C_range)
cv = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=42)
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=cv)
grid.fit(X, y)
print("The best parameters are %s with a score of %0.2f"
% (grid.best_params_, grid.best_score_))
# 現在,我們需要為二維數據下的所有參數擬合一個分類器(我們在這里使用一小部分參數,因為訓練需要一些時間)
C_2d_range = [1e-2, 1, 1e2]
gamma_2d_range = [1e-1, 1, 1e1]
classifiers = []
for C in C_2d_range:
for gamma in gamma_2d_range:
clf = SVC(C=C, gamma=gamma)
clf.fit(X_2d, y_2d)
classifiers.append((C, gamma, clf))
# #############################################################################
# 可視化
#
# 繪制參數效果
plt.figure(figsize=(8, 6))
xx, yy = np.meshgrid(np.linspace(-3, 3, 200), np.linspace(-3, 3, 200))
for (k, (C, gamma, clf)) in enumerate(classifiers):
# 在網格中評估決策函數的值
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 為這些參數可視化決策函數的值
plt.subplot(len(C_2d_range), len(gamma_2d_range), k + 1)
plt.title("gamma=10^%d, C=10^%d" % (np.log10(gamma), np.log10(C)),
size='medium')
# 可視化決策函數上的參數效果
plt.pcolormesh(xx, yy, -Z, cmap=plt.cm.RdBu)
plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y_2d, cmap=plt.cm.RdBu_r,
edgecolors='k')
plt.xticks(())
plt.yticks(())
plt.axis('tight')
scores = grid.cv_results_['mean_test_score'].reshape(len(C_range),
len(gamma_range))
# 繪制驗證準確率與gamma和C的函數關系的熱力圖
#
# 分數在熱色圖被編碼為顏色,從深紅色到亮黃色不等。由于最有趣的分數都位于0.92至0.97范圍內,因此我們使用自定義規范化器將顏色條中點設置為0.92,以便更輕松地可視化有趣范圍內分數值的微小變化,而不會殘酷地將所有低分值變為相同的顏色。
plt.figure(figsize=(8, 6))
plt.subplots_adjust(left=.2, right=0.95, bottom=0.15, top=0.95)
plt.imshow(scores, interpolation='nearest', cmap=plt.cm.hot,
norm=MidpointNormalize(vmin=0.2, midpoint=0.92))
plt.xlabel('gamma')
plt.ylabel('C')
plt.colorbar()
plt.xticks(np.arange(len(gamma_range)), gamma_range, rotation=45)
plt.yticks(np.arange(len(C_range)), C_range)
plt.title('Validation accuracy')
plt.show()
腳本的總運行時間:(0分鐘5.498秒)
