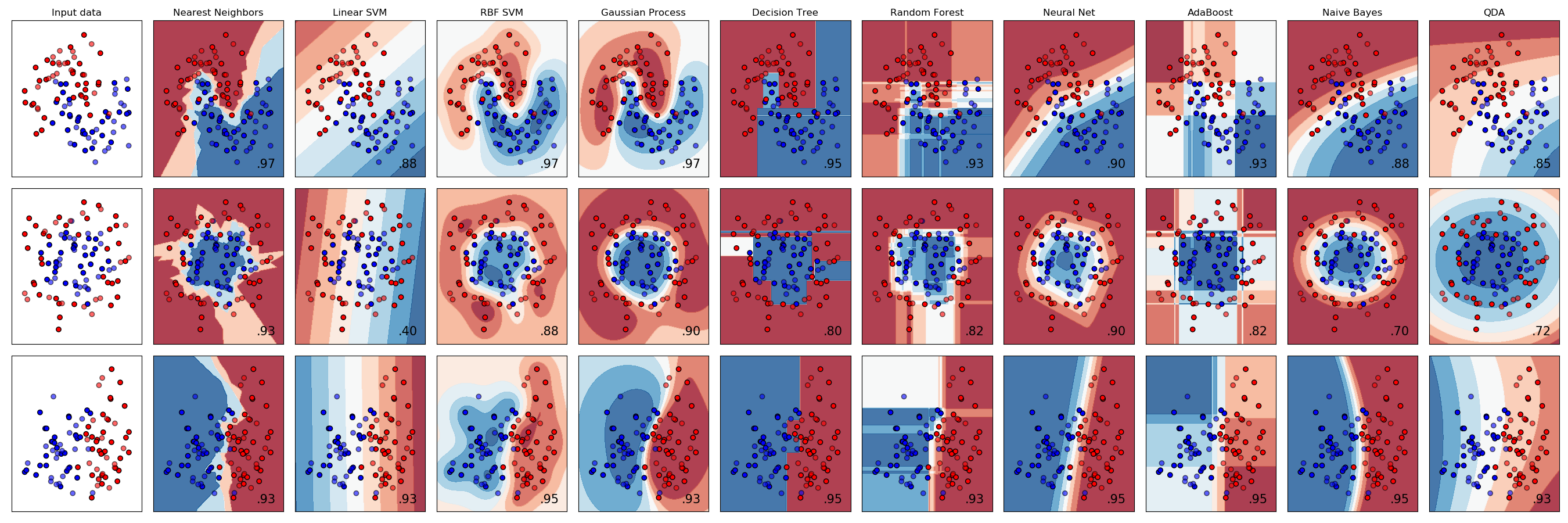
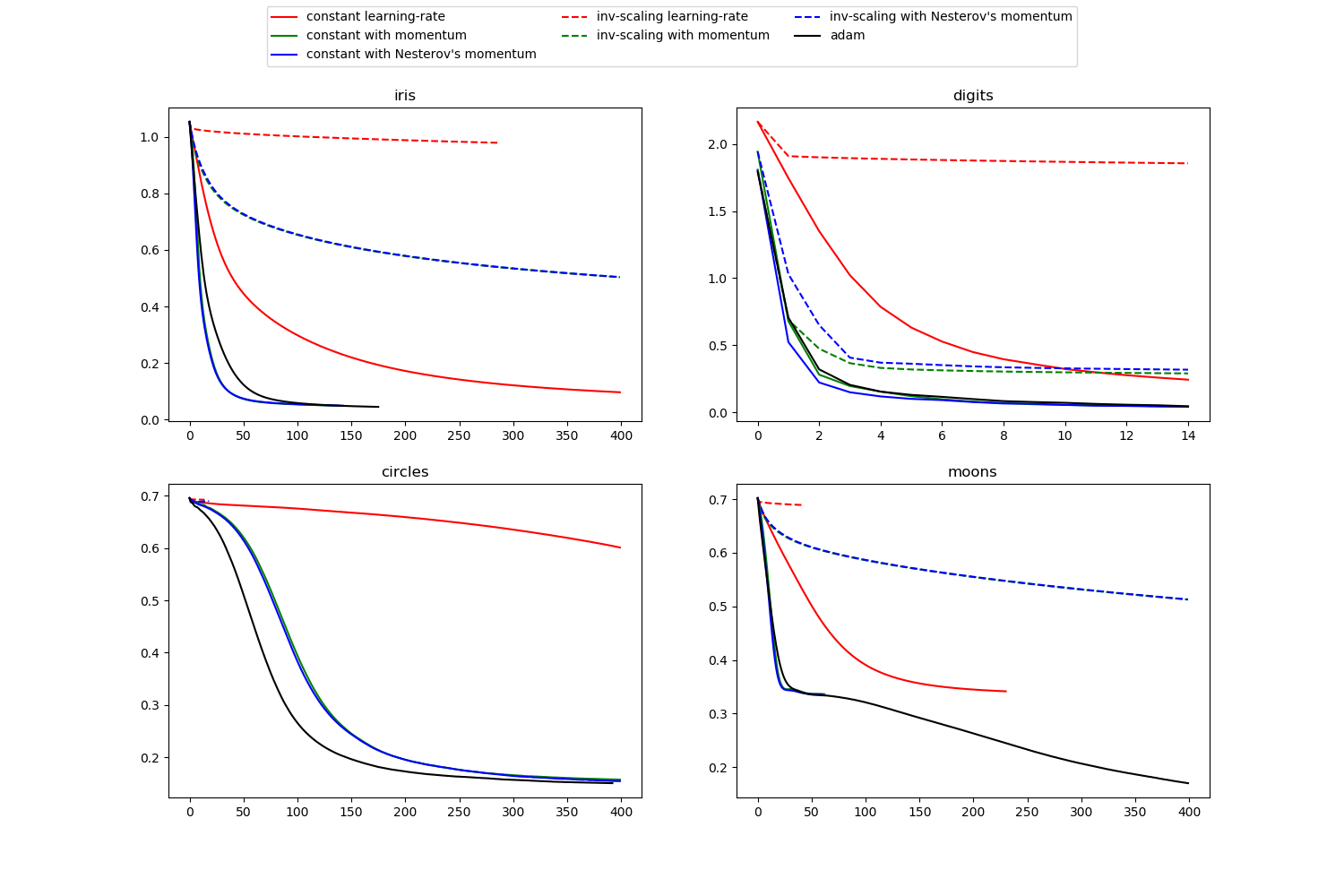
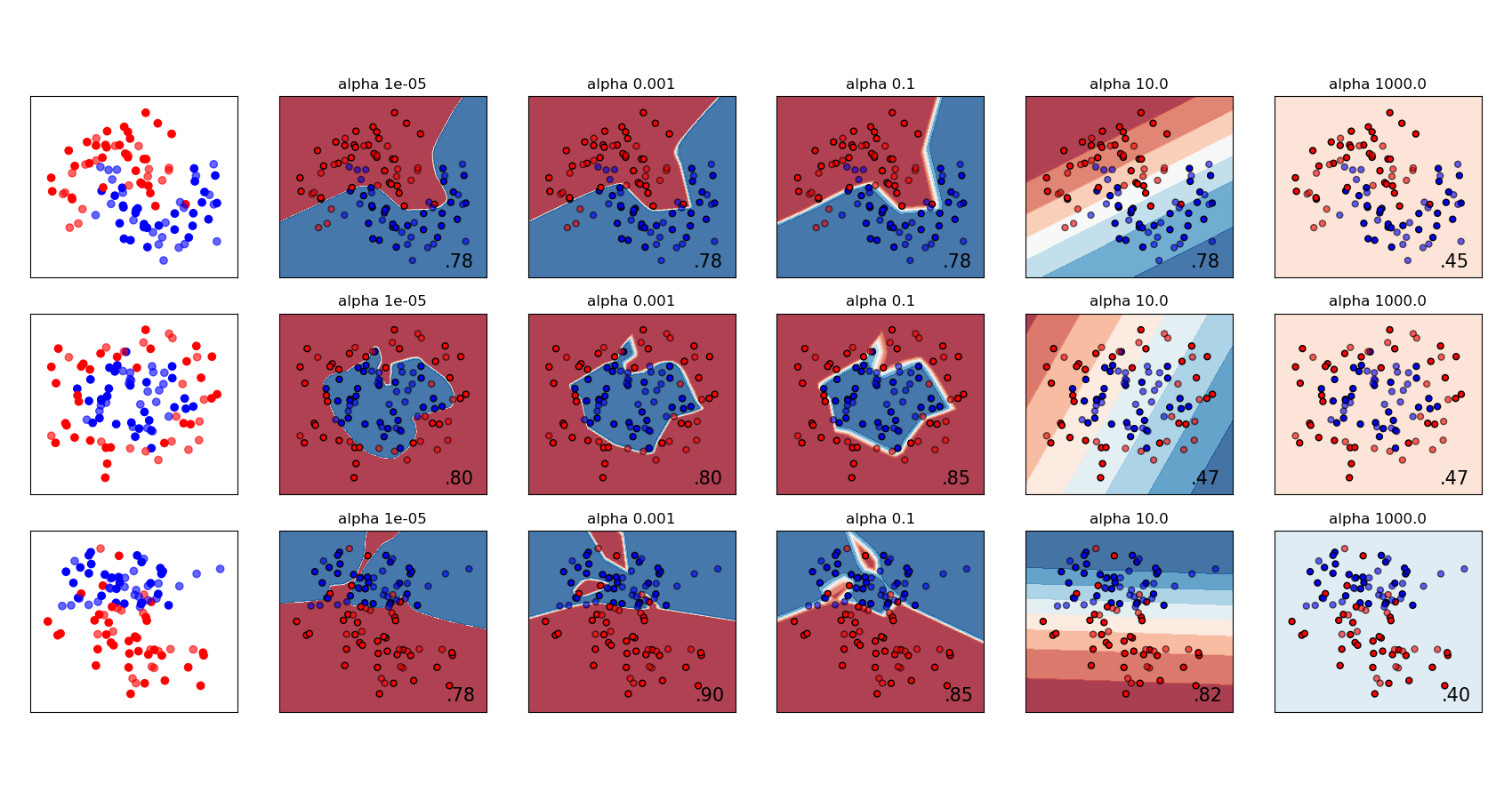
sklearn.neural_network.MLPClassifier?
class sklearn.neural_network.MLPClassifier(hidden_layer_sizes=(100, ), activation='relu', *, solver='adam', alpha=0.0001, batch_size='auto', learning_rate='constant', learning_rate_init=0.001, power_t=0.5, max_iter=200, shuffle=True, random_state=None, tol=0.0001, verbose=False, warm_start=False, momentum=0.9, nesterovs_momentum=True, early_stopping=False, validation_fraction=0.1, beta_1=0.9, beta_2=0.999, epsilon=1e-08, n_iter_no_change=10, max_fun=15000)
[源碼]
多層感知器分類器。
這個模型使用LBFGS或隨機梯度下降來優化對數損失函數。
版本0.18中的新功能。
| 參數 | 說明 |
|---|---|
| hidden_layer_sizes | tuple, length = n_layers - 2, default=(100,) 第i個元素代表第i個隱藏層中的神經元數量。 |
| activation | {‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, default=’relu’ 隱藏層的激活函數。 - 'identity',無操作激活,用于實現線性瓶頸,返回f(x)= x - 'logistic',logistic Sigmoid函數,返回f(x)= 1 / (1 + exp(x))。 - 'tanh',雙曲tan函數,返回f(x)= tanh(x)。 - 'relu',整流線性單位函數,返回f(x)= max(0,x) |
| solver | {‘lbfgs’, ‘sgd’, ‘adam’}, default=’adam’ 權重優化的求解器。 - “ lbfgs”是quasi-Newton方法族的優化程序。 - “ sgd”是指隨機梯度下降。 - “ adam”是指Kingma,Diederik和Jimmy Ba提出的基于隨機梯度的優化器 注意:就訓練時間和驗證準確率而言,默認求解器“ adam”在相對較大的數據集(具有數千個訓練樣本或更多)上的效果很好。但是,對于小型數據集,“ lbfgs”可以收斂得更快并且性能更好。 |
| alpha | float, default=0.0001 L2懲罰(正則項)參數。 |
| batch_size | int, default=’auto’ 隨機優化器的小批次的大小。如果求解器為“ lbfgs”,則分類器將不使用小批次批處理。設為“自動”時, batch_size=min(200, n_samples) |
| learning_rate | {‘constant’, ‘invscaling’, ‘adaptive’}, default=’constant’ 權重更新的學習速率表。 - ' constant '是一個恒定的學習速率,由' learning_rate_init '給出。 - “invscaling”通過使用“power_t”的縮放逆指數,逐步降低在每個時間步長“t”上的學習率。effective_learning_rate = learning_rate_init / pow(t, power_t) - 只要訓練損失持續減少,‘adaptive’將學習率保持在‘learning_rate_init’不變。每次連續兩個epoch不能減少至少tol的訓練損失,或者如果“early_stop”開啟,不能增加至少tol的驗證分數,則當前學習率要除以5。 僅在 solver='sgd'時使用。 |
| learning_rate_init | double, default=0.001 使用的初始學習率。它控制更新權重的步長。僅在Solver ='sgd'或'adam'時使用。 |
| power_t | double, default=0.5 反比例學習率的指數。當learning_rate設置為“ invscaling”時,它用于更新有效學習率。僅在Solver ='sgd'時使用。 |
| max_iter | int, default=200 最大迭代次數。求解器迭代直到收斂(由“ tol”決定)或這個迭代次數。對于隨機求解器(“ sgd”,“ adam”),請注意,這決定時期數(每個數據點將使用多少次),而不是梯度步數。 |
| shuffle | bool, default=True 是否在每次迭代中對樣本進行打亂。僅在Solver ='sgd'或'adam'時使用。 |
| random_state | int, RandomState instance, default=None 決定用于權重和偏差初始化的隨機數生成,如果使用了提前停止,則切分測試集和訓練集,并在solver ='sgd'或'adam'時批量采樣。在多個函數調用之間傳遞一個int值以獲得可重復的結果。請參閱詞匯表。 |
| tol | float, default=1e-4 優化公差。當 n_iter_no_change連續迭代的損失或分數沒有通過至少tol得到改善時,除非將learning_rate設置為‘adaptive’,否則將認為達到收斂并停止訓練。 |
| verbose | bool, default=False 是否將進度消息打印到標準輸出。 |
| warm_start | bool, default=False 設置為True時,請重用上一個調用的解決方案以擬合初始化,否則,只需擦除以前的解決方案即可。請參閱詞匯表。 |
| momentum | float, default=0.9 梯度下降更新的動量。應該在0到1之間。僅在solver ='sgd'時使用。 |
| nesterovs_momentum | boolean, default=True 是否使用內Nesterov的動量。僅在Solver ='sgd'且momentum> 0時使用。 |
| early_stopping | bool, default=False 當驗證準確率沒有提高時,是否使用提前停止來終止訓練。如果設置為true,它將自動預留10%的訓練數據作為驗證,并在 n_iter_no_change連續幾個時期,驗證準確率沒有提高至少tol時終止訓練 。除多標簽設置外,這個切分是分層的。僅在Solver ='sgd'或'adam'時有效 |
| validation_fraction | float, default=0.1 預留的訓練數據比例作為提前停止的驗證集。必須在0到1之間。僅當early_stopping為True時使用 |
| beta_1 | float, default=0.9 adam第一矩向量估計的指數衰減率,應在[0,1)范圍內。僅在solver ='adam'時使用 |
| beta_2 | float, default=0.999 adam第二矩向量估計的指數衰減率,應在[0,1)范圍內。僅在solver ='adam'時使用 |
| epsilon | float, default=1e-8 adam中數值穩定性的值。僅在solver ='adam'時使用 |
| n_iter_no_change | int, default=10 不滿足 tol改進的最大時期數。僅在Solver ='sgd'或'adam'時有效0.20版中的新功能。 |
| max_fun | int, default=15000 僅在Solver ='lbfgs'時使用。損失函數調用的最大次數。求解器迭代直到收斂(由“ tol”確定),迭代次數達到max_iter或這個損失函數調用的次數。請注意,損失函數調用的次數將大于或等于 MLPClassifier的迭代次數。0.22版中的新功能。 |
| 屬性 | 說明 |
|---|---|
| classes_ | ndarray or list of ndarray of shape (n_classes,) 每個輸出的類別標簽。 |
| loss_ | float 用損失函數計算的當前損失。 |
| coefs_ | list, length n_layers - 1 列表中的第i個元素表示與第i層相對應的權重矩陣。 |
| intercepts_ | list, length n_layers - 1 列表中的第i個元素表示與層i + 1對應的偏差向量。 |
| n_iter_ | int, 求解程序已運行的迭代次數。 |
| n_layers_ | int 層數。 |
| n_outputs_ | int 輸出數量。 |
| out_activation_ | string 輸出激活函數的名稱。 |
注
MLPClassifier進行迭代訓練,因為在每個時間步長都計算了損失函數相對于模型參數的偏導數以更新參數。
它還可以在損失函數中添加正則項,縮小模型參數以防止過擬合。
這個實現適用于表示為浮點值的密集numpy數組或稀疏矩陣數組的數據。
參考文獻
Hinton, Geoffrey E.
“Connectionist learning procedures.” Artificial intelligence 40.1 (1989): 185-234.
Glorot, Xavier, and Yoshua Bengio. “Understanding the difficulty of
training deep feedforward neural networks.” International Conference on Artificial Intelligence and Statistics. 2010.
He, Kaiming, et al. “Delving deep into rectifiers: Surpassing human-level
performance on imagenet classification.” arXiv preprint arXiv:1502.01852 (2015).
Kingma, Diederik, and Jimmy Ba. “Adam: A method for stochastic
optimization.” arXiv preprint arXiv:1412.6980 (2014).
示例
>>> from sklearn.neural_network import MLPClassifier
>>> from sklearn.datasets import make_classification
>>> from sklearn.model_selection import train_test_split
>>> X, y = make_classification(n_samples=100, random_state=1)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,
... random_state=1)
>>> clf = MLPClassifier(random_state=1, max_iter=300).fit(X_train, y_train)
>>> clf.predict_proba(X_test[:1])
array([[0.038..., 0.961...]])
>>> clf.predict(X_test[:5, :])
array([1, 0, 1, 0, 1])
>>> clf.score(X_test, y_test)
0.8...
方法
| 方法 | 說明 |
|---|---|
fit(X,y) |
根據矩陣X和標簽y的數據擬合模型 |
get_params([deep]) |
獲取這個估計器的參數。 |
predict(X) |
使用多層感知器分類器進行預測 |
predict_log_proba(X) |
返回概率估計的對數。 |
predict_proba(X) |
概率估計。 |
score(X, y[, sample_weight]) |
返回給定測試數據和標簽上的平均準確率。 |
set_params(**params) |
設置這個估計器的參數。 |
__init__(hidden_layer_sizes=(100, ), activation='relu', *, solver='adam', alpha=0.0001, batch_size='auto', learning_rate='constant', learning_rate_init=0.001, power_t=0.5, max_iter=200, shuffle=True, random_state=None, tol=0.0001, verbose=False, warm_start=False, momentum=0.9, nesterovs_momentum=True, early_stopping=False, validation_fraction=0.1, beta_1=0.9, beta_2=0.999, epsilon=1e-08, n_iter_no_change=10, max_fun=15000)
[源碼]
初始化self。詳情可參閱 type(self)的幫助。
fit(X, y)
[源碼]
根據矩陣X和標簽y的數據擬合模型
| 參數 | 說明 |
|---|---|
| X | ndarray or sparse matrix of shape (n_samples, n_features) 輸入數據。 |
| y | ndarray, shape (n_samples,) or (n_samples, n_outputs) 目標值(分類中的類別標簽,回歸中的實數)。 |
| 返回值 | 說明 |
|---|---|
| self | returns a trained MLP model. |
get_params(deep=True)
[源碼]
獲取這個估計器的參數。
| 參數 | 說明 |
|---|---|
| deep | bool, default=True 如果為True,則將返回這個估計器的參數和所包含的估計器子對象。 |
| 返回值 | 說明 |
|---|---|
| params | mapping of string to any 參數名映射到其值 |
property partial_fit
使用給定數據的單次迭代更新模型。
| 參數 | 說明 |
|---|---|
| X | {array-like, sparse matrix}, shape (n_samples, n_features) 輸入數據。 |
| y | array-like, shape (n_samples,) 目標值。 |
| classes | array, shape (n_classes), default None 類越過所有對partial_fit的調用。可以通過 np.unique(y_all)獲得,其中y_all是整個數據集的目標向量。第一次調用partial_fit時需要此參數,在后續調用中可以將其省略。請注意,y不需要包含classes中的所有標簽。 |
| 返回值 | 說明 |
|---|---|
| self | returns a trained MLP model. |
predict(X)
[源碼]
使用多層感知器分類器進行預測
| 參數 | 說明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 輸入數據。 |
| 返回值 | 說明 |
|---|---|
| y | ndarray, shape (n_samples,) or (n_samples, n_classes) 預測的類別。 |
predict_log_proba(X)
[源碼]
返回概率估計的對數。
| 參數 | 說明 |
|---|---|
| X | ndarray of shape (n_samples, n_features) 輸入數據。 |
| 返回值 | 說明 |
|---|---|
| log_y_prob | ndarray of shape (n_samples, n_classes) 模型中每個類別的樣本的預期對數概率,類別按 self.classes_中的順序排序 。等效于log(predict_proba(X)) |
predict_proba(X)
[源碼]
概率估計。
| 參數 | 說明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 輸入數據。 |
| 返回值 | 說明 |
|---|---|
| y_prob | ndarray of shape (n_samples, n_classes) 模型中每個類別的樣本的預測概率,類別按 self.classes_中的順序排序。 |
score(X, y, sample_weight=None)
[源碼]
返回給定測試數據和標簽上的平均準確率。
在多標簽分類中,這是子集準確性,這是一個嚴格的指標,因為您需要為每個樣本正確預測每個標簽集。
| 參數 | 說明 |
|---|---|
| X | array-like of shape (n_samples, n_features) 測試樣本 |
| y | array-like of shape (n_samples,) or (n_samples, n_outputs) X的真實標簽。 |
| sample_weight | array-like of shape (n_samples,), default=None 樣本權重 |
| 返回值 | 說明 |
|---|---|
| score | float self.predict(X)關于y的平均準確率。 |
set_params(**params)
[源碼]
設置這個估計器的參數。
該方法適用于簡單的估計器以及嵌套對象(例如pipelines)。后者具有形式參數 <component>__<parameter>,以便可以更新嵌套對象的每個組件。
| 參數 | 說明 |
|---|---|
| **params | dict 估計器參數 |
| 返回值 | 說明 |
|---|---|
| self | object 估計器實例 |