稀疏逆協方差估計?
使用 GraphicalLasso 估計器從少量樣本中學習協方差和稀疏精度。
要估計概率模型(如高斯模型),估計精度矩陣,即逆協方差矩陣,與估計協方差矩陣一樣重要。實際上,高斯模型是由精度矩陣參數化的。
為了在良好的恢復條件下,我們從一個稀疏逆協方差矩陣模型中對數據進行了采樣。此外,我們還確保數據不存在太大的相關性(限制了精度矩陣的最大系數),并確保在精度矩陣中有一個無法恢復的小系數。此外,通過少量的觀測,可以更容易地恢復相關矩陣而不是協方差,因此我們對時間序列進行了縮放。
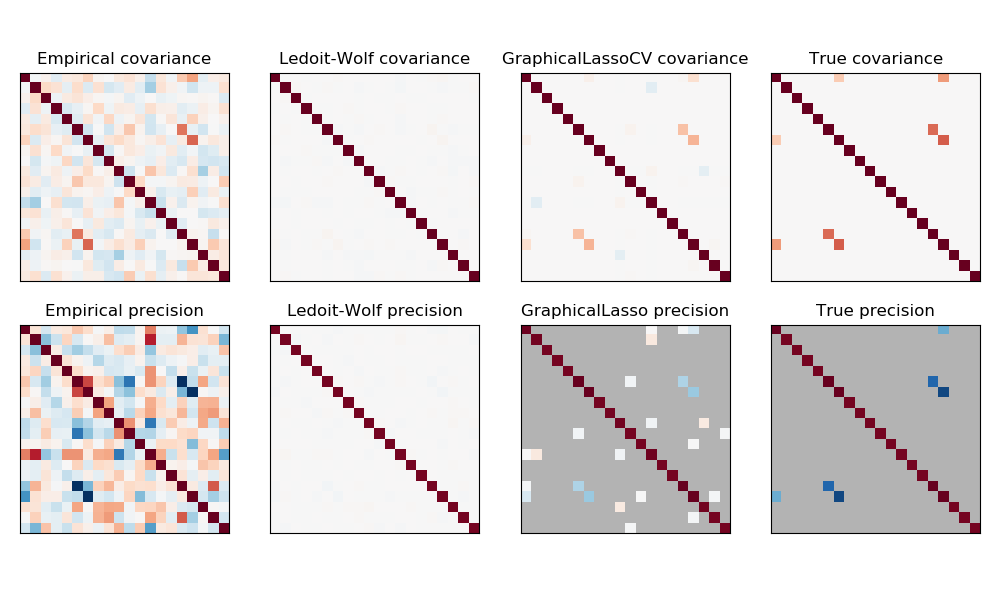
在這里,樣本數略大于維數,因此經驗協方差仍然是可逆的。然而,由于觀測結果有很強的相關性,經驗協方差矩陣是不受限制的的,因此它的逆--經驗精度矩陣--離實際真是情況很遠。
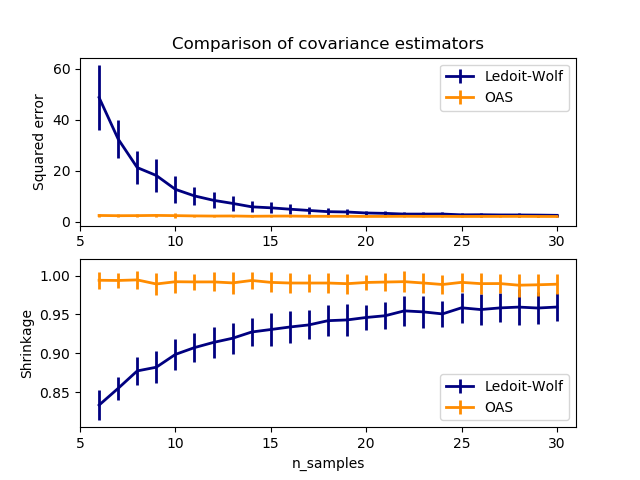
如果我們使用l2 shrinkage,就像 Ledoit-Wolf 估計那樣,由于樣本數量很小,我們需要進行大量的收縮。因此,Ledoit-Wolf的精度相當接近真實精度,即離對角線不遠,但偏離對角線的結構是丟失的。
l1-懲罰的估計器可以恢復這種非對角結構的一部分。它學習了稀疏的精度。它無法恢復精確的稀疏模式:它檢測到太多的非零系數。然而,估計的L1的最高非零系數對應于真是情況中的非零系數。最后,L1精度估計的系數偏向于零:由于懲罰,它們都小于相應的真實值,如圖中所示。
注意,精確矩陣的顏色范圍被調整以提高圖形的可讀性。沒有顯示經驗精度的全部范圍。
print(__doc__)
# author: Gael Varoquaux <gael.varoquaux@inria.fr>
# License: BSD 3 clause
# Copyright: INRIA
import numpy as np
from scipy import linalg
from sklearn.datasets import make_sparse_spd_matrix
from sklearn.covariance import GraphicalLassoCV, ledoit_wolf
import matplotlib.pyplot as plt
# #############################################################################
# Generate the data
n_samples = 60
n_features = 20
prng = np.random.RandomState(1)
prec = make_sparse_spd_matrix(n_features, alpha=.98,
smallest_coef=.4,
largest_coef=.7,
random_state=prng)
cov = linalg.inv(prec)
d = np.sqrt(np.diag(cov))
cov /= d
cov /= d[:, np.newaxis]
prec *= d
prec *= d[:, np.newaxis]
X = prng.multivariate_normal(np.zeros(n_features), cov, size=n_samples)
X -= X.mean(axis=0)
X /= X.std(axis=0)
# #############################################################################
# Estimate the covariance
emp_cov = np.dot(X.T, X) / n_samples
model = GraphicalLassoCV()
model.fit(X)
cov_ = model.covariance_
prec_ = model.precision_
lw_cov_, _ = ledoit_wolf(X)
lw_prec_ = linalg.inv(lw_cov_)
# #############################################################################
# Plot the results
plt.figure(figsize=(10, 6))
plt.subplots_adjust(left=0.02, right=0.98)
# plot the covariances
covs = [('Empirical', emp_cov), ('Ledoit-Wolf', lw_cov_),
('GraphicalLassoCV', cov_), ('True', cov)]
vmax = cov_.max()
for i, (name, this_cov) in enumerate(covs):
plt.subplot(2, 4, i + 1)
plt.imshow(this_cov, interpolation='nearest', vmin=-vmax, vmax=vmax,
cmap=plt.cm.RdBu_r)
plt.xticks(())
plt.yticks(())
plt.title('%s covariance' % name)
# plot the precisions
precs = [('Empirical', linalg.inv(emp_cov)), ('Ledoit-Wolf', lw_prec_),
('GraphicalLasso', prec_), ('True', prec)]
vmax = .9 * prec_.max()
for i, (name, this_prec) in enumerate(precs):
ax = plt.subplot(2, 4, i + 5)
plt.imshow(np.ma.masked_equal(this_prec, 0),
interpolation='nearest', vmin=-vmax, vmax=vmax,
cmap=plt.cm.RdBu_r)
plt.xticks(())
plt.yticks(())
plt.title('%s precision' % name)
if hasattr(ax, 'set_facecolor'):
ax.set_facecolor('.7')
else:
ax.set_axis_bgcolor('.7')
# plot the model selection metric
plt.figure(figsize=(4, 3))
plt.axes([.2, .15, .75, .7])
plt.plot(model.cv_alphas_, np.mean(model.grid_scores_, axis=1), 'o-')
plt.axvline(model.alpha_, color='.5')
plt.title('Model selection')
plt.ylabel('Cross-validation score')
plt.xlabel('alpha')
plt.show()
腳本的總運行時間:(0分0.755秒)
