收縮協方差估計:LedoitWolf VS OAS和極大似然?
當處理協方差估計時,通常的方法是使用極大似然估計。例如 sklearn.covariance.EmpiricalCovariance,這是不偏不倚的。當給出許多觀測結果時,它收斂到真實的(總體)協方差。然而,正則化也可能是有益的,以減少它的方差;這反過來又帶來一些偏差。這個例子說明了在 Shrunk Covariance估計中使用的簡單正則化。特別是如何設置正則化的數量,即如何選擇偏差-方差權衡。
在這里,我們比較了三種方法:
根據潛在收縮參數的網格,通過三折交叉驗證的可能性來設置參數。 Ledoit和Wolf提出的求漸近最優正則化參數(最小MSE準則)的封閉公式,得到了 sklearn.covariance.LedoitWolf協方差估計。關于 Ledoit-Wolf收縮的改進, sklearn.covariance.OAS,由Chen等人提出。在假設數據是高斯的情況下,特別是對于小樣本,它的收斂性要好得多。
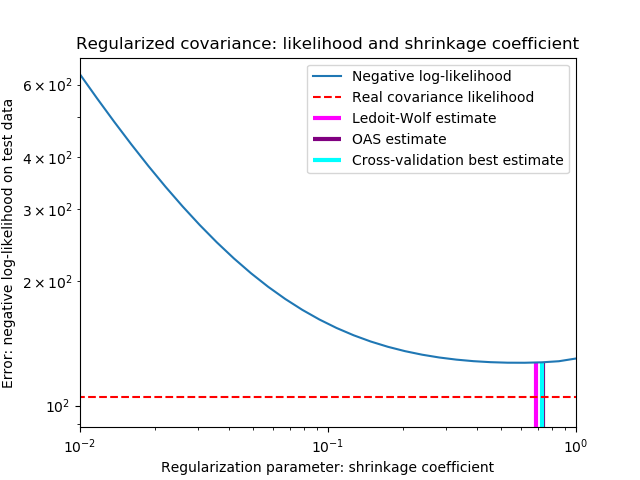
為了量化估計誤差,我們對收縮參數的不同值繪制了不可見數據的可能性圖。我們還通過LedoitWolf和OAS估計的交叉驗證進行選擇顯示。
請注意,極大似然估計值沒有收縮,因此表現不佳。Ledoit-Wolf估計的表現非常好,因為它接近最優,而且計算成本不高。在這個例子中,OAS的估計更遠一點。有趣的是,這兩種方法的性能都優于交叉驗證,因為交叉驗證在計算上開銷最大。
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg
from sklearn.covariance import LedoitWolf, OAS, ShrunkCovariance, \
log_likelihood, empirical_covariance
from sklearn.model_selection import GridSearchCV
# #############################################################################
# Generate sample data
n_features, n_samples = 40, 20
np.random.seed(42)
base_X_train = np.random.normal(size=(n_samples, n_features))
base_X_test = np.random.normal(size=(n_samples, n_features))
# Color samples
coloring_matrix = np.random.normal(size=(n_features, n_features))
X_train = np.dot(base_X_train, coloring_matrix)
X_test = np.dot(base_X_test, coloring_matrix)
# #############################################################################
# Compute the likelihood on test data
# spanning a range of possible shrinkage coefficient values
shrinkages = np.logspace(-2, 0, 30)
negative_logliks = [-ShrunkCovariance(shrinkage=s).fit(X_train).score(X_test)
for s in shrinkages]
# under the ground-truth model, which we would not have access to in real
# settings
real_cov = np.dot(coloring_matrix.T, coloring_matrix)
emp_cov = empirical_covariance(X_train)
loglik_real = -log_likelihood(emp_cov, linalg.inv(real_cov))
# #############################################################################
# Compare different approaches to setting the parameter
# GridSearch for an optimal shrinkage coefficient
tuned_parameters = [{'shrinkage': shrinkages}]
cv = GridSearchCV(ShrunkCovariance(), tuned_parameters)
cv.fit(X_train)
# Ledoit-Wolf optimal shrinkage coefficient estimate
lw = LedoitWolf()
loglik_lw = lw.fit(X_train).score(X_test)
# OAS coefficient estimate
oa = OAS()
loglik_oa = oa.fit(X_train).score(X_test)
# #############################################################################
# Plot results
fig = plt.figure()
plt.title("Regularized covariance: likelihood and shrinkage coefficient")
plt.xlabel('Regularization parameter: shrinkage coefficient')
plt.ylabel('Error: negative log-likelihood on test data')
# range shrinkage curve
plt.loglog(shrinkages, negative_logliks, label="Negative log-likelihood")
plt.plot(plt.xlim(), 2 * [loglik_real], '--r',
label="Real covariance likelihood")
# adjust view
lik_max = np.amax(negative_logliks)
lik_min = np.amin(negative_logliks)
ymin = lik_min - 6. * np.log((plt.ylim()[1] - plt.ylim()[0]))
ymax = lik_max + 10. * np.log(lik_max - lik_min)
xmin = shrinkages[0]
xmax = shrinkages[-1]
# LW likelihood
plt.vlines(lw.shrinkage_, ymin, -loglik_lw, color='magenta',
linewidth=3, label='Ledoit-Wolf estimate')
# OAS likelihood
plt.vlines(oa.shrinkage_, ymin, -loglik_oa, color='purple',
linewidth=3, label='OAS estimate')
# best CV estimator likelihood
plt.vlines(cv.best_estimator_.shrinkage, ymin,
-cv.best_estimator_.score(X_test), color='cyan',
linewidth=3, label='Cross-validation best estimate')
plt.ylim(ymin, ymax)
plt.xlim(xmin, xmax)
plt.legend()
plt.show()
腳本的總運行時間:(0分0.439秒)
