魯棒協方差估計與Mahalanobis距離相關性?
在高斯分布數據上用Mahalanobis距離表示協方差估計的一個例子。
對于高斯分布的數據,觀測值到 分布模式的距離可以用它的Mahalanobis距離:,其中μ和Σ是基礎高斯分布的位置和協方差。
在實踐中,μ和Σ被一些估計所取代。通常的協方差極大似然估計對數據集中存在的異常值非常敏感, 因此,對應于mahalanobis距離。我們最好使用一個穩健的協方差估計器,以保證估計能夠抵抗數據集中的“erroneous”觀測,并且相關的Mahalanobis距離準確地反映了觀測的真正組織。
最小協方差行列式估計是一個魯棒的高分解點(即它可以用來估計高污染數據集的協方差矩陣), 最多可達個離群點)的協方差估計。其思想是找出個觀測值,其經驗協方差有最小的行列式,產生一個“純”的觀測子集,從中計算位置和協方差的標準估計。
最小協方差行列式是在 P.J.Rousseuw in [1]中被提到。
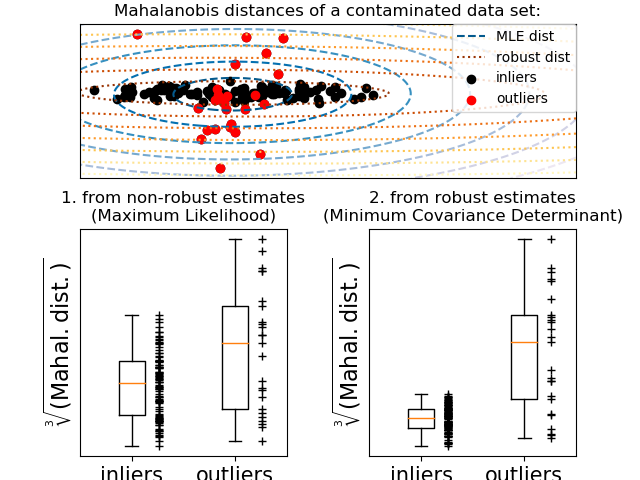
此示例說明了Mahalanobis距離如何受到離群數據的影響:從污染分布中提取的觀測結果與實際的高斯分布的觀測無法區分。利用基于MCD的mahalanobis距離,這兩個種群可以區分開來。相關的應用是孤立點檢測、觀測排序、聚類。為了便于可視化,Mahalanobis距離的立方根用箱線圖表示, 如 Wilson and Hilferty[2]中建議的一樣。
[1] P. J. Rousseeuw. Least median of squares regression. J. Am
Stat Ass, 79:871, 1984.
[2] Wilson, E. B., & Hilferty, M. M. (1931). The distribution of chi-square.
Proceedings of the National Academy of Sciences of the United States of America, 17, 684-688.
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.covariance import EmpiricalCovariance, MinCovDet
n_samples = 125
n_outliers = 25
n_features = 2
# generate data
gen_cov = np.eye(n_features)
gen_cov[0, 0] = 2.
X = np.dot(np.random.randn(n_samples, n_features), gen_cov)
# add some outliers
outliers_cov = np.eye(n_features)
outliers_cov[np.arange(1, n_features), np.arange(1, n_features)] = 7.
X[-n_outliers:] = np.dot(np.random.randn(n_outliers, n_features), outliers_cov)
# fit a Minimum Covariance Determinant (MCD) robust estimator to data
robust_cov = MinCovDet().fit(X)
# compare estimators learnt from the full data set with true parameters
emp_cov = EmpiricalCovariance().fit(X)
# #############################################################################
# Display results
fig = plt.figure()
plt.subplots_adjust(hspace=-.1, wspace=.4, top=.95, bottom=.05)
# Show data set
subfig1 = plt.subplot(3, 1, 1)
inlier_plot = subfig1.scatter(X[:, 0], X[:, 1],
color='black', label='inliers')
outlier_plot = subfig1.scatter(X[:, 0][-n_outliers:], X[:, 1][-n_outliers:],
color='red', label='outliers')
subfig1.set_xlim(subfig1.get_xlim()[0], 11.)
subfig1.set_title("Mahalanobis distances of a contaminated data set:")
# Show contours of the distance functions
xx, yy = np.meshgrid(np.linspace(plt.xlim()[0], plt.xlim()[1], 100),
np.linspace(plt.ylim()[0], plt.ylim()[1], 100))
zz = np.c_[xx.ravel(), yy.ravel()]
mahal_emp_cov = emp_cov.mahalanobis(zz)
mahal_emp_cov = mahal_emp_cov.reshape(xx.shape)
emp_cov_contour = subfig1.contour(xx, yy, np.sqrt(mahal_emp_cov),
cmap=plt.cm.PuBu_r,
linestyles='dashed')
mahal_robust_cov = robust_cov.mahalanobis(zz)
mahal_robust_cov = mahal_robust_cov.reshape(xx.shape)
robust_contour = subfig1.contour(xx, yy, np.sqrt(mahal_robust_cov),
cmap=plt.cm.YlOrBr_r, linestyles='dotted')
subfig1.legend([emp_cov_contour.collections[1], robust_contour.collections[1],
inlier_plot, outlier_plot],
['MLE dist', 'robust dist', 'inliers', 'outliers'],
loc="upper right", borderaxespad=0)
plt.xticks(())
plt.yticks(())
# Plot the scores for each point
emp_mahal = emp_cov.mahalanobis(X - np.mean(X, 0)) ** (0.33)
subfig2 = plt.subplot(2, 2, 3)
subfig2.boxplot([emp_mahal[:-n_outliers], emp_mahal[-n_outliers:]], widths=.25)
subfig2.plot(np.full(n_samples - n_outliers, 1.26),
emp_mahal[:-n_outliers], '+k', markeredgewidth=1)
subfig2.plot(np.full(n_outliers, 2.26),
emp_mahal[-n_outliers:], '+k', markeredgewidth=1)
subfig2.axes.set_xticklabels(('inliers', 'outliers'), size=15)
subfig2.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
subfig2.set_title("1. from non-robust estimates\n(Maximum Likelihood)")
plt.yticks(())
robust_mahal = robust_cov.mahalanobis(X - robust_cov.location_) ** (0.33)
subfig3 = plt.subplot(2, 2, 4)
subfig3.boxplot([robust_mahal[:-n_outliers], robust_mahal[-n_outliers:]],
widths=.25)
subfig3.plot(np.full(n_samples - n_outliers, 1.26),
robust_mahal[:-n_outliers], '+k', markeredgewidth=1)
subfig3.plot(np.full(n_outliers, 2.26),
robust_mahal[-n_outliers:], '+k', markeredgewidth=1)
subfig3.axes.set_xticklabels(('inliers', 'outliers'), size=15)
subfig3.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
subfig3.set_title("2. from robust estimates\n(Minimum Covariance Determinant)")
plt.yticks(())
plt.show()
腳本的總運行時間:(0分0.298秒)
