單調約束?
這個例子說明了單調約束對梯度提升估計器的影響。
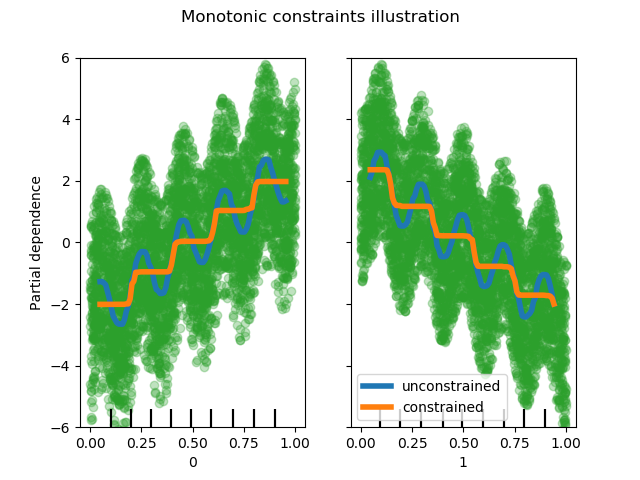
我們創建了一個人工數據集,其中目標值一般與第一個特征正相關(具有一些隨機和非隨機變化),而在一般情況下與第二個特征呈負相關。
通過在學習過程中對特征施加正(增)或負(減)約束,估計器能夠正確地跟隨總趨勢,而不受變化的影響。
此示例的靈感來源于 XGBoost documentation.
from sklearn.experimental import enable_hist_gradient_boosting # noqa
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.inspection import plot_partial_dependence
import numpy as np
import matplotlib.pyplot as plt
print(__doc__)
rng = np.random.RandomState(0)
n_samples = 5000
f_0 = rng.rand(n_samples) # positive correlation with y
f_1 = rng.rand(n_samples) # negative correlation with y
X = np.c_[f_0, f_1]
noise = rng.normal(loc=0.0, scale=0.01, size=n_samples)
y = (5 * f_0 + np.sin(10 * np.pi * f_0) -
5 * f_1 - np.cos(10 * np.pi * f_1) +
noise)
fig, ax = plt.subplots()
# Without any constraint
gbdt = HistGradientBoostingRegressor()
gbdt.fit(X, y)
disp = plot_partial_dependence(
gbdt, X, features=[0, 1],
line_kw={'linewidth': 4, 'label': 'unconstrained'},
ax=ax)
# With positive and negative constraints
gbdt = HistGradientBoostingRegressor(monotonic_cst=[1, -1])
gbdt.fit(X, y)
plot_partial_dependence(
gbdt, X, features=[0, 1],
feature_names=('First feature\nPositive constraint',
'Second feature\nNegtive constraint'),
line_kw={'linewidth': 4, 'label': 'constrained'},
ax=disp.axes_)
for f_idx in (0, 1):
disp.axes_[0, f_idx].plot(X[:, f_idx], y, 'o', alpha=.3, zorder=-1)
disp.axes_[0, f_idx].set_ylim(-6, 6)
plt.legend()
fig.suptitle("Monotonic constraints illustration")
plt.show()
腳本的總運行時間:(0分0.876秒)
