高斯混合模型正弦曲線?
此示例演示了高斯混合模型的行為,該模型適合于未從混合高斯隨機變量中取樣的數據。該數據集由100個點按照噪聲正弦曲線松散間隔形成。因此,高斯分量的數目不存在真正的值。
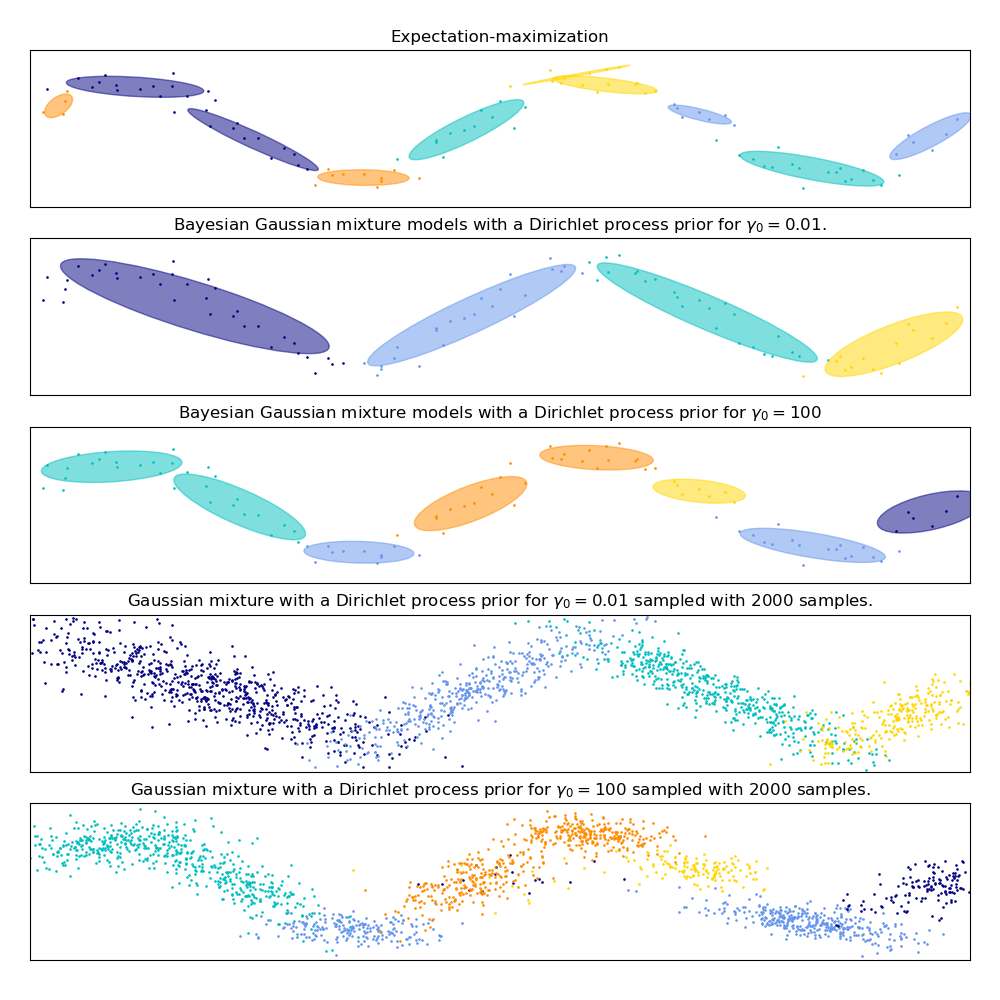
第一個模型是一個經典的高斯混合模型,它包含10個分量,擬合期望最大化算法。
第二個模型是帶Dirichlet過程先驗擬合和變分推理的貝葉斯高斯混合模型。聚集先驗的低值使模型傾向于活躍成分的低值。該模型“決定”將其建模能力集中在數據集結構的總體圖上:用非對角協方差矩陣建模的交替方向點群。這些交替方向大致捕捉原始正弦信號的交替性質。
第三種模型也是帶有Dirichlet過程先驗的貝葉斯高斯混合模型,但這一次的聚集先驗值較高,給模型更多的自由度來對數據的細粒度結構進行建模。結果是一個具有更多活躍成分的混合體,類似于第一個模型,在第一個模型中,我們任意地將成分的數量固定為10。
哪一種模式是最好的,取決于主觀判斷:我們是更喜歡模型能夠捕捉一個總體圖, 以此來總結和解釋絕大多數的數據結構, 并且或略細節, 還是喜歡這個模型與信號的高密度區域密切相關?
最后兩個圖片展示了我們如何從最后兩個模型中取樣。得到的樣本分布看起來與原始數據分布不完全一樣。這種差異主要來自于我們所使用的模型所產生的近似誤差,該模型假設數據是由有限個高斯分量而不是連續的噪聲正弦曲線生成的。
import itertools
import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn import mixture
print(__doc__)
color_iter = itertools.cycle(['navy', 'c', 'cornflowerblue', 'gold',
'darkorange'])
def plot_results(X, Y, means, covariances, index, title):
splot = plt.subplot(5, 1, 1 + index)
for i, (mean, covar, color) in enumerate(zip(
means, covariances, color_iter)):
v, w = linalg.eigh(covar)
v = 2. * np.sqrt(2.) * np.sqrt(v)
u = w[0] / linalg.norm(w[0])
# as the DP will not use every component it has access to
# unless it needs it, we shouldn't plot the redundant
# components.
if not np.any(Y == i):
continue
plt.scatter(X[Y == i, 0], X[Y == i, 1], .8, color=color)
# Plot an ellipse to show the Gaussian component
angle = np.arctan(u[1] / u[0])
angle = 180. * angle / np.pi # convert to degrees
ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
ell.set_clip_box(splot.bbox)
ell.set_alpha(0.5)
splot.add_artist(ell)
plt.xlim(-6., 4. * np.pi - 6.)
plt.ylim(-5., 5.)
plt.title(title)
plt.xticks(())
plt.yticks(())
def plot_samples(X, Y, n_components, index, title):
plt.subplot(5, 1, 4 + index)
for i, color in zip(range(n_components), color_iter):
# as the DP will not use every component it has access to
# unless it needs it, we shouldn't plot the redundant
# components.
if not np.any(Y == i):
continue
plt.scatter(X[Y == i, 0], X[Y == i, 1], .8, color=color)
plt.xlim(-6., 4. * np.pi - 6.)
plt.ylim(-5., 5.)
plt.title(title)
plt.xticks(())
plt.yticks(())
# Parameters
n_samples = 100
# Generate random sample following a sine curve
np.random.seed(0)
X = np.zeros((n_samples, 2))
step = 4. * np.pi / n_samples
for i in range(X.shape[0]):
x = i * step - 6.
X[i, 0] = x + np.random.normal(0, 0.1)
X[i, 1] = 3. * (np.sin(x) + np.random.normal(0, .2))
plt.figure(figsize=(10, 10))
plt.subplots_adjust(bottom=.04, top=0.95, hspace=.2, wspace=.05,
left=.03, right=.97)
# Fit a Gaussian mixture with EM using ten components
gmm = mixture.GaussianMixture(n_components=10, covariance_type='full',
max_iter=100).fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, 0,
'Expectation-maximization')
dpgmm = mixture.BayesianGaussianMixture(
n_components=10, covariance_type='full', weight_concentration_prior=1e-2,
weight_concentration_prior_type='dirichlet_process',
mean_precision_prior=1e-2, covariance_prior=1e0 * np.eye(2),
init_params="random", max_iter=100, random_state=2).fit(X)
plot_results(X, dpgmm.predict(X), dpgmm.means_, dpgmm.covariances_, 1,
"Bayesian Gaussian mixture models with a Dirichlet process prior "
r"for $\gamma_0=0.01$.")
X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(X_s, y_s, dpgmm.n_components, 0,
"Gaussian mixture with a Dirichlet process prior "
r"for $\gamma_0=0.01$ sampled with $2000$ samples.")
dpgmm = mixture.BayesianGaussianMixture(
n_components=10, covariance_type='full', weight_concentration_prior=1e+2,
weight_concentration_prior_type='dirichlet_process',
mean_precision_prior=1e-2, covariance_prior=1e0 * np.eye(2),
init_params="kmeans", max_iter=100, random_state=2).fit(X)
plot_results(X, dpgmm.predict(X), dpgmm.means_, dpgmm.covariances_, 2,
"Bayesian Gaussian mixture models with a Dirichlet process prior "
r"for $\gamma_0=100$")
X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(X_s, y_s, dpgmm.n_components, 1,
"Gaussian mixture with a Dirichlet process prior "
r"for $\gamma_0=100$ sampled with $2000$ samples.")
plt.show()
腳本的總運行時間:(0分0.515秒)
