Mauna Loa CO2數據的高斯過程回歸(GPR)?
此示例基于“用于機器學習的高斯過程”第5.4.3節[RW 2006]。他給出了一個在對數邊際似然上用梯度上升法進行復雜核工程和超參數優化的例子。這些數據包括1958年至2001年期間在夏威 Mauna Loa 觀測站收集的大氣二氧化碳平均濃度(按體積計算,以百萬分之數(ppmv)計)。目的是模擬二氧化碳濃度隨時間t的變化。
內核由幾個術語組成,它們負責解釋信號的不同屬性:
一個長期的,平穩的上升趨勢可以用RBF核來解釋。長尺度較大的徑向基函數(RBF)內核強制成平滑,沒有強制趨勢上升,這就留給GP選擇。長度、比例尺和振幅是自由的超參數。
季節性因素,由定期的 ExpSineSquared 內核解釋,固定周期為1年。 該周期分量的長度尺度控制其平滑度是一個自由參數。 為了使準確周期性的衰減,采用帶有RBF內核的產品。 該RBF組件的長度尺寸控制衰減時間,并且是另一個自由參數。
較小的中期不規則性將由 RationalQuadratic 核來解釋, RationalQuadratic 內核組件的長度尺度和 alpha 參數決定長度尺度的擴散性。 根據[RW2006],這些不規則性可以更好地由 RationalQuadratic 來解釋, 而不是 RBF 核,這可能是因為它可以容納幾個長度尺度。
“noise(噪聲)” 一詞,由一個 RBF 內核貢獻組成,它將解釋相關的噪聲分量,如局部天氣現象以及 WhiteKernel 對白噪聲的貢獻。 相對幅度和RBF的長度尺度是進一步的自由參數。
在減去目標平均值后最大化對數邊際似然產生下列內核,其中LML為-83.214:
34.4**2 * RBF(length_scale=41.8)
+ 3.27**2 * RBF(length_scale=180) * ExpSineSquared(length_scale=1.44,
periodicity=1)
+ 0.446**2 * RationalQuadratic(alpha=17.7, length_scale=0.957)
+ 0.197**2 * RBF(length_scale=0.138) + WhiteKernel(noise_level=0.0336)
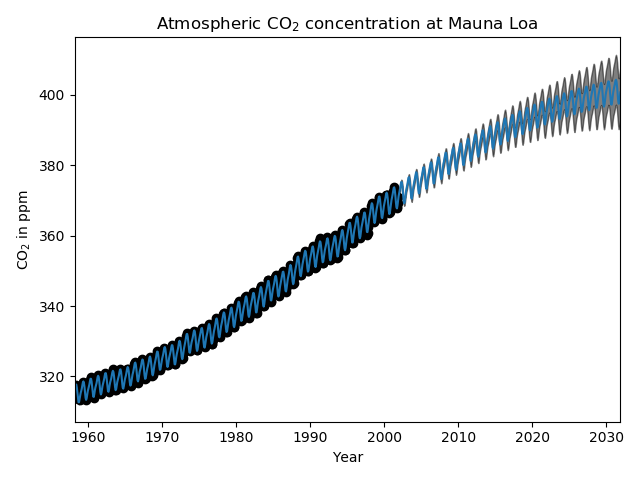
因此,大多數目標信號(34.4ppm)由長期上升趨勢(長度為41.8年)解釋。 周期分量的振幅為3.27ppm,衰減時間為180年,長度為1.44。 長時間的衰變時間表明我們在當地非常接近周期性的季節性成分。 相關噪聲的幅度為0.197ppm,長度為0.138年,白噪聲貢獻為0.197ppm。 因此,整體噪聲水平非常小,表明該模型可以很好地解釋數據。 該圖還顯示,該模型直到2015年左右才能做出置信度比較高的預測。
GPML kernel: 66**2 * RBF(length_scale=67) + 2.4**2 * RBF(length_scale=90) * ExpSineSquared(length_scale=1.3, periodicity=1) + 0.66**2 * RationalQuadratic(alpha=0.78, length_scale=1.2) + 0.18**2 * RBF(length_scale=0.134) + WhiteKernel(noise_level=0.0361)
Log-marginal-likelihood: 155.006
Learned kernel: 2.59**2 * RBF(length_scale=51) + 0.257**2 * RBF(length_scale=137) * ExpSineSquared(length_scale=2.15, periodicity=1) + 0.118**2 * RationalQuadratic(alpha=2.32, length_scale=70.6) + 0.03**2 * RBF(length_scale=1.01) + WhiteKernel(noise_level=0.001)
Log-marginal-likelihood: 1161.609
# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
#
# License: BSD 3 clause
import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels \
import RBF, WhiteKernel, RationalQuadratic, ExpSineSquared
print(__doc__)
def load_mauna_loa_atmospheric_co2():
ml_data = fetch_openml(data_id=41187)
months = []
ppmv_sums = []
counts = []
y = ml_data.data[:, 0]
m = ml_data.data[:, 1]
month_float = y + (m - 1) / 12
ppmvs = ml_data.target
for month, ppmv in zip(month_float, ppmvs):
if not months or month != months[-1]:
months.append(month)
ppmv_sums.append(ppmv)
counts.append(1)
else:
# aggregate monthly sum to produce average
ppmv_sums[-1] += ppmv
counts[-1] += 1
months = np.asarray(months).reshape(-1, 1)
avg_ppmvs = np.asarray(ppmv_sums) / counts
return months, avg_ppmvs
X, y = load_mauna_loa_atmospheric_co2()
# Kernel with parameters given in GPML book
k1 = 66.0**2 * RBF(length_scale=67.0) # long term smooth rising trend
k2 = 2.4**2 * RBF(length_scale=90.0) \
* ExpSineSquared(length_scale=1.3, periodicity=1.0) # seasonal component
# medium term irregularity
k3 = 0.66**2 \
* RationalQuadratic(length_scale=1.2, alpha=0.78)
k4 = 0.18**2 * RBF(length_scale=0.134) \
+ WhiteKernel(noise_level=0.19**2) # noise terms
kernel_gpml = k1 + k2 + k3 + k4
gp = GaussianProcessRegressor(kernel=kernel_gpml, alpha=0,
optimizer=None, normalize_y=True)
gp.fit(X, y)
print("GPML kernel: %s" % gp.kernel_)
print("Log-marginal-likelihood: %.3f"
% gp.log_marginal_likelihood(gp.kernel_.theta))
# Kernel with optimized parameters
k1 = 50.0**2 * RBF(length_scale=50.0) # long term smooth rising trend
k2 = 2.0**2 * RBF(length_scale=100.0) \
* ExpSineSquared(length_scale=1.0, periodicity=1.0,
periodicity_bounds="fixed") # seasonal component
# medium term irregularities
k3 = 0.5**2 * RationalQuadratic(length_scale=1.0, alpha=1.0)
k4 = 0.1**2 * RBF(length_scale=0.1) \
+ WhiteKernel(noise_level=0.1**2,
noise_level_bounds=(1e-3, np.inf)) # noise terms
kernel = k1 + k2 + k3 + k4
gp = GaussianProcessRegressor(kernel=kernel, alpha=0,
normalize_y=True)
gp.fit(X, y)
print("\nLearned kernel: %s" % gp.kernel_)
print("Log-marginal-likelihood: %.3f"
% gp.log_marginal_likelihood(gp.kernel_.theta))
X_ = np.linspace(X.min(), X.max() + 30, 1000)[:, np.newaxis]
y_pred, y_std = gp.predict(X_, return_std=True)
# Illustration
plt.scatter(X, y, c='k')
plt.plot(X_, y_pred)
plt.fill_between(X_[:, 0], y_pred - y_std, y_pred + y_std,
alpha=0.5, color='k')
plt.xlim(X_.min(), X_.max())
plt.xlabel("Year")
plt.ylabel(r"CO$_2$ in ppm")
plt.title(r"Atmospheric CO$_2$ concentration at Mauna Loa")
plt.tight_layout()
plt.show()
腳本的總運行時間:(0分9.429秒)
