保險索賠的推斷回歸?
此示例演示了Poisson、Gamma和Tweedie回歸在法國汽車第三方責任索賠數據集上的使用，并受R教程[1]的啟發。
在這個數據集中，每個樣本對應于保險單，即保險公司和個人(投保人)內的合同。可用的功能包括駕駛年齡，車輛年齡，車輛動力等。
幾個定義：索賠是指投保人向保險公司提出的賠償保險損失的請求。索賠額是保險公司必須支付的金額。風險敞口是以年數為單位的某一特定保單的保險承保期限。
在這里，我們的目標是預測期望值，也就是每一敞口單位索賠總額的平均值，也稱為純保費。
有幾種可能做到這一點，其中兩種是：
用泊松分布對索賠數量進行建模，將每項索賠的平均索賠額(也稱為嚴重程度)建模為Gamma分布，并將兩者的預測相乘，以得到索賠總額。 直接模擬每次曝光的總索賠額，通常使用Twedie Power的Twedie分布。
在這個例子中，我們將說明這兩種方法。我們首先定義一些用于加載數據和可視化結果的輔助函數。
1 A. Noll, R. Salzmann and M.V. Wuthrich, Case Study: French Motor Third-Party Liability Claims (November 8, 2018). doi:10.2139/ssrn.3164764
print(__doc__)
# Authors: Christian Lorentzen <lorentzen.ch@gmail.com>
# Roman Yurchak <rth.yurchak@gmail.com>
# Olivier Grisel <olivier.grisel@ensta.org>
# License: BSD 3 clause
from functools import partial
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.compose import ColumnTransformer
from sklearn.linear_model import PoissonRegressor, GammaRegressor
from sklearn.linear_model import TweedieRegressor
from sklearn.metrics import mean_tweedie_deviance
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder
from sklearn.preprocessing import StandardScaler, KBinsDiscretizer
from sklearn.metrics import mean_absolute_error, mean_squared_error, auc
def load_mtpl2(n_samples=100000):
"""Fetch the French Motor Third-Party Liability Claims dataset.
Parameters
----------
n_samples: int, default=100000
number of samples to select (for faster run time). Full dataset has
678013 samples.
"""
# freMTPL2freq dataset from https://www.openml.org/d/41214
df_freq = fetch_openml(data_id=41214, as_frame=True)['data']
df_freq['IDpol'] = df_freq['IDpol'].astype(np.int)
df_freq.set_index('IDpol', inplace=True)
# freMTPL2sev dataset from https://www.openml.org/d/41215
df_sev = fetch_openml(data_id=41215, as_frame=True)['data']
# sum ClaimAmount over identical IDs
df_sev = df_sev.groupby('IDpol').sum()
df = df_freq.join(df_sev, how="left")
df["ClaimAmount"].fillna(0, inplace=True)
# unquote string fields
for column_name in df.columns[df.dtypes.values == np.object]:
df[column_name] = df[column_name].str.strip("'")
return df.iloc[:n_samples]
def plot_obs_pred(df, feature, weight, observed, predicted, y_label=None,
title=None, ax=None, fill_legend=False):
"""Plot observed and predicted - aggregated per feature level.
Parameters
----------
df : DataFrame
input data
feature: str
a column name of df for the feature to be plotted
weight : str
column name of df with the values of weights or exposure
observed : str
a column name of df with the observed target
predicted : DataFrame
a dataframe, with the same index as df, with the predicted target
fill_legend : bool, default=False
whether to show fill_between legend
"""
# aggregate observed and predicted variables by feature level
df_ = df.loc[:, [feature, weight]].copy()
df_["observed"] = df[observed] * df[weight]
df_["predicted"] = predicted * df[weight]
df_ = (
df_.groupby([feature])[[weight, "observed", "predicted"]]
.sum()
.assign(observed=lambda x: x["observed"] / x[weight])
.assign(predicted=lambda x: x["predicted"] / x[weight])
)
ax = df_.loc[:, ["observed", "predicted"]].plot(style=".", ax=ax)
y_max = df_.loc[:, ["observed", "predicted"]].values.max() * 0.8
p2 = ax.fill_between(
df_.index,
0,
y_max * df_[weight] / df_[weight].values.max(),
color="g",
alpha=0.1,
)
if fill_legend:
ax.legend([p2], ["{} distribution".format(feature)])
ax.set(
ylabel=y_label if y_label is not None else None,
title=title if title is not None else "Train: Observed vs Predicted",
)
def score_estimator(
estimator, X_train, X_test, df_train, df_test, target, weights,
tweedie_powers=None,
):
"""Evaluate an estimator on train and test sets with different metrics"""
metrics = [
("D2 explained", None), # Use default scorer if it exists
("mean abs. error", mean_absolute_error),
("mean squared error", mean_squared_error),
]
if tweedie_powers:
metrics += [(
"mean Tweedie dev p={:.4f}".format(power),
partial(mean_tweedie_deviance, power=power)
) for power in tweedie_powers]
res = []
for subset_label, X, df in [
("train", X_train, df_train),
("test", X_test, df_test),
]:
y, _weights = df[target], df[weights]
for score_label, metric in metrics:
if isinstance(estimator, tuple) and len(estimator) == 2:
# Score the model consisting of the product of frequency and
# severity models.
est_freq, est_sev = estimator
y_pred = est_freq.predict(X) * est_sev.predict(X)
else:
y_pred = estimator.predict(X)
if metric is None:
if not hasattr(estimator, "score"):
continue
score = estimator.score(X, y, sample_weight=_weights)
else:
score = metric(y, y_pred, sample_weight=_weights)
res.append(
{"subset": subset_label, "metric": score_label, "score": score}
)
res = (
pd.DataFrame(res)
.set_index(["metric", "subset"])
.score.unstack(-1)
.round(4)
.loc[:, ['train', 'test']]
)
return res
加載數據集、基本特征提取和目標定義
我們通過將包含索賠數量(ClaimNb)的freMTPL2freq表與包含相同策略ID(IDpol)的索賠額(ClaimAMount)的freMTPL2sev表連接起來，構建freMTPL2數據集。
df = load_mtpl2(n_samples=60000)
# Note: filter out claims with zero amount, as the severity model
# requires strictly positive target values.
df.loc[(df["ClaimAmount"] == 0) & (df["ClaimNb"] >= 1), "ClaimNb"] = 0
# Correct for unreasonable observations (that might be data error)
# and a few exceptionally large claim amounts
df["ClaimNb"] = df["ClaimNb"].clip(upper=4)
df["Exposure"] = df["Exposure"].clip(upper=1)
df["ClaimAmount"] = df["ClaimAmount"].clip(upper=200000)
log_scale_transformer = make_pipeline(
FunctionTransformer(func=np.log),
StandardScaler()
)
column_trans = ColumnTransformer(
[
("binned_numeric", KBinsDiscretizer(n_bins=10),
["VehAge", "DrivAge"]),
("onehot_categorical", OneHotEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"]),
("passthrough_numeric", "passthrough",
["BonusMalus"]),
("log_scaled_numeric", log_scale_transformer,
["Density"]),
],
remainder="drop",
)
X = column_trans.fit_transform(df)
# Insurances companies are interested in modeling the Pure Premium, that is
# the expected total claim amount per unit of exposure for each policyholder
# in their portfolio:
df["PurePremium"] = df["ClaimAmount"] / df["Exposure"]
# This can be indirectly approximated by a 2-step modeling: the product of the
# Frequency times the average claim amount per claim:
df["Frequency"] = df["ClaimNb"] / df["Exposure"]
df["AvgClaimAmount"] = df["ClaimAmount"] / np.fmax(df["ClaimNb"], 1)
with pd.option_context("display.max_columns", 15):
print(df[df.ClaimAmount > 0].head())
/home/circleci/project/sklearn/datasets/_openml.py:754: UserWarning: Version 1 of dataset freMTPL2freq is inactive, meaning that issues have been found in the dataset. Try using a newer version from this URL: https://www.openml.org/data/v1/download/20649148/freMTPL2freq.arff
warn("Version {} of dataset {} is inactive, meaning that issues have "
/home/circleci/project/sklearn/datasets/_openml.py:754: UserWarning: Version 1 of dataset freMTPL2sev is inactive, meaning that issues have been found in the dataset. Try using a newer version from this URL: https://www.openml.org/data/v1/download/20649149/freMTPL2sev.arff
warn("Version {} of dataset {} is inactive, meaning that issues have "
/home/circleci/project/sklearn/preprocessing/_discretization.py:200: UserWarning: Bins whose width are too small (i.e., <= 1e-8) in feature 0 are removed. Consider decreasing the number of bins.
warnings.warn('Bins whose width are too small (i.e., <= '
ClaimNb Exposure Area VehPower VehAge DrivAge BonusMalus VehBrand \
IDpol
139 1.0 0.75 F 7.0 1.0 61.0 50.0 B12
190 1.0 0.14 B 12.0 5.0 50.0 60.0 B12
414 1.0 0.14 E 4.0 0.0 36.0 85.0 B12
424 2.0 0.62 F 10.0 0.0 51.0 100.0 B12
463 1.0 0.31 A 5.0 0.0 45.0 50.0 B12
VehGas Density Region ClaimAmount PurePremium Frequency \
IDpol
139 Regular 27000.0 R11 303.00 404.000000 1.333333
190 Diesel 56.0 R25 1981.84 14156.000000 7.142857
414 Regular 4792.0 R11 1456.55 10403.928571 7.142857
424 Regular 27000.0 R11 10834.00 17474.193548 3.225806
463 Regular 12.0 R73 3986.67 12860.225806 3.225806
AvgClaimAmount
IDpol
139 303.00
190 1981.84
414 1456.55
424 5417.00
463 3986.67
頻率模型-泊松分布
索賠數量(ClaimNb)是一個正整數(包括0)。因此，這個目標可以用泊松分布來建模。然后假定為在給定時間間隔內以恒定速率發生的離散事件的數目(Exposure，以年為單位)。在這里，我們建立了頻率 y = ClaimNb / Exposure的模型，該模型仍然是一個(尺度)泊松分布，并以 Exposure a作為sample_weight.。
df_train, df_test, X_train, X_test = train_test_split(df, X, random_state=0)
# The parameters of the model are estimated by minimizing the Poisson deviance
# on the training set via a quasi-Newton solver: l-BFGS. Some of the features
# are collinear, we use a weak penalization to avoid numerical issues.
glm_freq = PoissonRegressor(alpha=1e-3, max_iter=400)
glm_freq.fit(X_train, df_train["Frequency"],
sample_weight=df_train["Exposure"])
scores = score_estimator(
glm_freq,
X_train,
X_test,
df_train,
df_test,
target="Frequency",
weights="Exposure",
)
print("Evaluation of PoissonRegressor on target Frequency")
print(scores)
Evaluation of PoissonRegressor on target Frequency
subset train test
metric
D2 explained 0.0590 0.0579
mean abs. error 0.1706 0.1661
mean squared error 0.3041 0.3043
我們可以以駕駛員年齡(DrivAge)、車輛年齡(VehAge)和保險獎金/malus(BonusMalus)來比較觀察值和預測值。
fig, ax = plt.subplots(ncols=2, nrows=2, figsize=(16, 8))
fig.subplots_adjust(hspace=0.3, wspace=0.2)
plot_obs_pred(
df=df_train,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_train),
y_label="Claim Frequency",
title="train data",
ax=ax[0, 0],
)
plot_obs_pred(
df=df_test,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[0, 1],
fill_legend=True
)
plot_obs_pred(
df=df_test,
feature="VehAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 0],
fill_legend=True
)
plot_obs_pred(
df=df_test,
feature="BonusMalus",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 1],
fill_legend=True
)
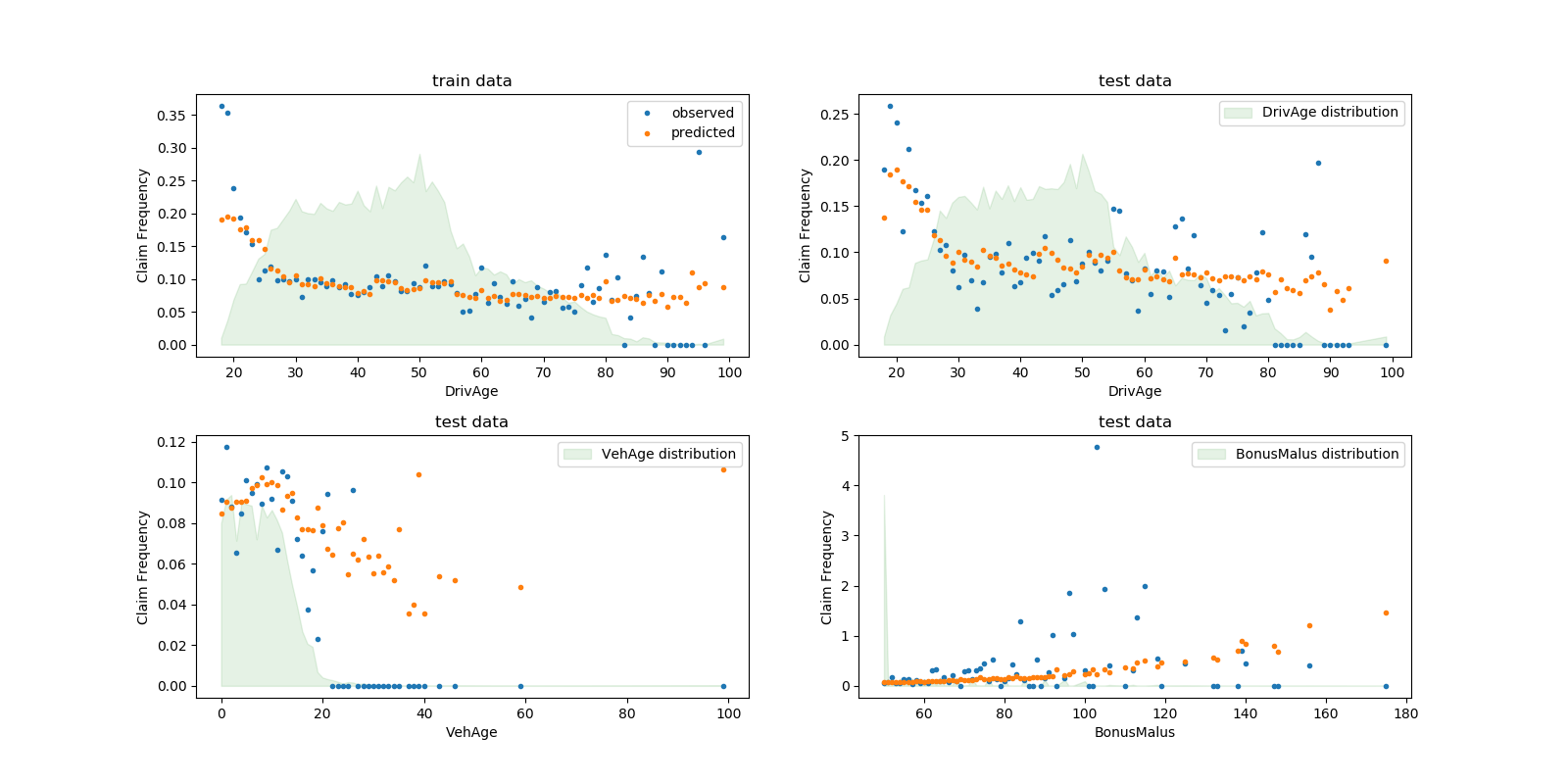根據觀測資料，30歲以下駕駛員發生事故的頻率較高，且與BonusMalus變量呈正相關。我們的模型能夠在很大程度上正確地模擬這種行為。
嚴重程度模型-伽瑪分布
平均索賠金額或嚴重程度(AvgClaimAMount)可以在大致顯示為遵循Gamma分布。我們用與頻率模型相同的特征來擬合嚴重程度的GLM模型。
注意：
Gamm分布支持，而不是時，我們過濾掉 ClaimAmount == 0。我們使用 ClaimNb作為sample_weight來說明包含多個索賠的保單。
mask_train = df_train["ClaimAmount"] > 0
mask_test = df_test["ClaimAmount"] > 0
glm_sev = GammaRegressor(alpha=10., max_iter=10000)
glm_sev.fit(
X_train[mask_train.values],
df_train.loc[mask_train, "AvgClaimAmount"],
sample_weight=df_train.loc[mask_train, "ClaimNb"],
)
scores = score_estimator(
glm_sev,
X_train[mask_train.values],
X_test[mask_test.values],
df_train[mask_train],
df_test[mask_test],
target="AvgClaimAmount",
weights="ClaimNb",
)
print("Evaluation of GammaRegressor on target AvgClaimAmount")
print(scores)
Evaluation of GammaRegressor on target AvgClaimAmount
subset train test
metric
D2 explained 4.300000e-03 -1.380000e-02
mean abs. error 1.699197e+03 2.027923e+03
mean squared error 4.548147e+07 6.094863e+07
在這里，測試數據的分數需要謹慎，因為它們比訓練數據要差得多，這表明盡管有很強的正則化，但這些數據任然過擬合。
請注意，得出的模型是每項索賠的平均索賠額。因此，它以至少有一項索賠為條件，一般不能用來預測每一保單的平均索賠額。
print("Mean AvgClaim Amount per policy: %.2f "
% df_train["AvgClaimAmount"].mean())
print("Mean AvgClaim Amount | NbClaim > 0: %.2f"
% df_train["AvgClaimAmount"][df_train["AvgClaimAmount"] > 0].mean())
print("Predicted Mean AvgClaim Amount | NbClaim > 0: %.2f"
% glm_sev.predict(X_train).mean())
Mean AvgClaim Amount per policy: 97.89
Mean AvgClaim Amount | NbClaim > 0: 1899.60
Predicted Mean AvgClaim Amount | NbClaim > 0: 1884.40
我們可以直觀地比較觀察值和預測值，并根據駕駛員的年齡進行匯總(DrivAge)。
fig, ax = plt.subplots(ncols=1, nrows=2, figsize=(16, 6))
plot_obs_pred(
df=df_train.loc[mask_train],
feature="DrivAge",
weight="Exposure",
observed="AvgClaimAmount",
predicted=glm_sev.predict(X_train[mask_train.values]),
y_label="Average Claim Severity",
title="train data",
ax=ax[0],
)
plot_obs_pred(
df=df_test.loc[mask_test],
feature="DrivAge",
weight="Exposure",
observed="AvgClaimAmount",
predicted=glm_sev.predict(X_test[mask_test.values]),
y_label="Average Claim Severity",
title="test data",
ax=ax[1],
fill_legend=True
)
plt.tight_layout()
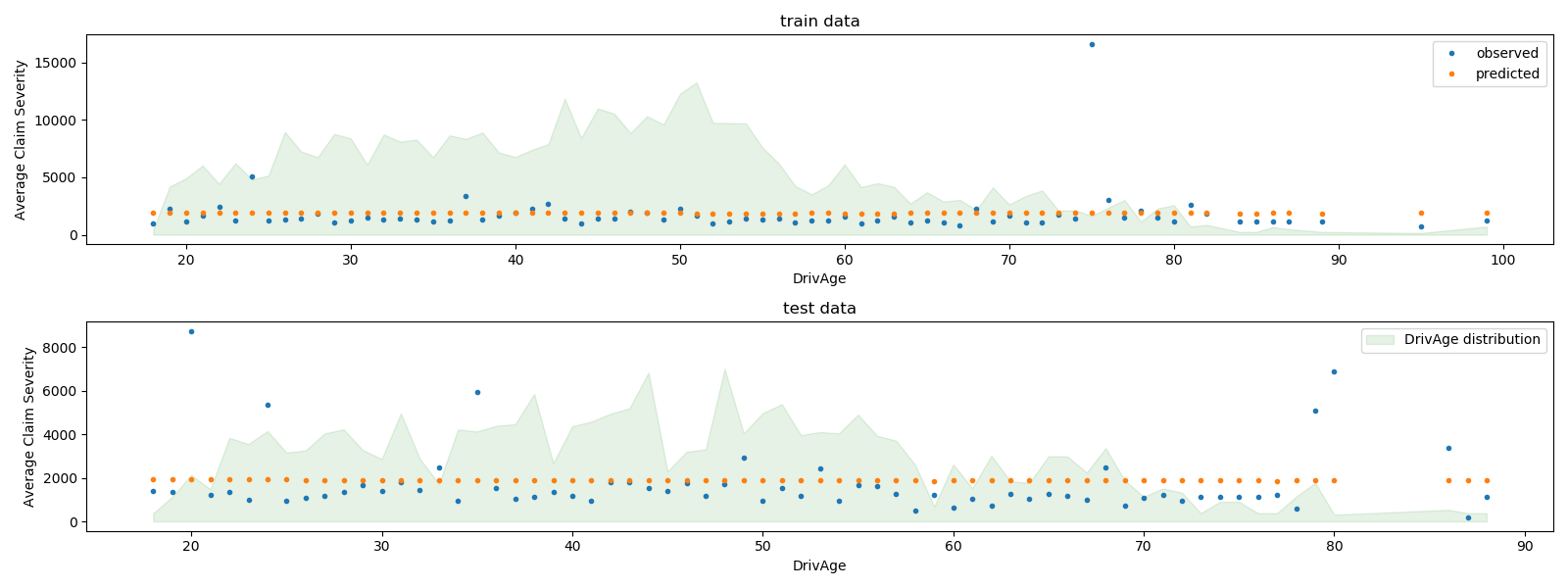總的來說，司機年齡(DrivAge)對索賠嚴重程度的影響很小，無論是在觀察數據還是預測數據中。
基于產品模型 vs 單Tweedie回歸的純保險費建模
如導言所述，每單位曝露的總索賠額可以通過對嚴重程度模型的預測，模擬為頻率模型預測的乘積。
或者，可以直接用唯一的復合Poisson Gamma廣義線性模型(帶有日志鏈接函數)來模擬總損失。該模型是具有“冪”參數的Twedie GLM的特例。在此，我們將Tweedie模型的power參數預先固定為有效范圍內的任意值(1.9)。理想情況下，人們可以通過網格搜索來選擇這個值，方法是最小化Tweedie模型的對數似然，但是不幸的是，當前的實現不允許這樣做(還)。
我們將比較兩種方法的性能。為了量化這兩種模型的性能，可以計算訓練和測試數據的平均偏差，假設索賠總額的復合Poisson-Gamma分布。這與power參數介于1和2之間的Tweedie分布等價。
sklearn.metrics.mean_tweedie_deviance 依賴power參數。在這里，我們計算了一個可能值的網格的平均偏差，并對模型進行了并行比較。我們用相同的power值來比較它們。理想情況下，我們希望無論power如何，一種模式將始終優于另一種模式。
glm_pure_premium = TweedieRegressor(power=1.9, alpha=.1, max_iter=10000)
glm_pure_premium.fit(X_train, df_train["PurePremium"],
sample_weight=df_train["Exposure"])
tweedie_powers = [1.5, 1.7, 1.8, 1.9, 1.99, 1.999, 1.9999]
scores_product_model = score_estimator(
(glm_freq, glm_sev),
X_train,
X_test,
df_train,
df_test,
target="PurePremium",
weights="Exposure",
tweedie_powers=tweedie_powers,
)
scores_glm_pure_premium = score_estimator(
glm_pure_premium,
X_train,
X_test,
df_train,
df_test,
target="PurePremium",
weights="Exposure",
tweedie_powers=tweedie_powers
)
scores = pd.concat([scores_product_model, scores_glm_pure_premium],
axis=1, sort=True,
keys=('Product Model', 'TweedieRegressor'))
print("Evaluation of the Product Model and the Tweedie Regressor "
"on target PurePremium")
with pd.option_context('display.expand_frame_repr', False):
print(scores)
Evaluation of the Product Model and the Tweedie Regressor on target PurePremium
Product Model TweedieRegressor
subset train test train test
D2 explained NaN NaN 2.550000e-02 2.480000e-02
mean Tweedie dev p=1.5000 8.217990e+01 8.640200e+01 7.960820e+01 8.618700e+01
mean Tweedie dev p=1.7000 3.833750e+01 3.920430e+01 3.737390e+01 3.917460e+01
mean Tweedie dev p=1.8000 3.106910e+01 3.148750e+01 3.047900e+01 3.148130e+01
mean Tweedie dev p=1.9000 3.396250e+01 3.420610e+01 3.360070e+01 3.420830e+01
mean Tweedie dev p=1.9900 1.989243e+02 1.996420e+02 1.986911e+02 1.996461e+02
mean Tweedie dev p=1.9990 1.886429e+03 1.892749e+03 1.886206e+03 1.892753e+03
mean Tweedie dev p=1.9999 1.876452e+04 1.882692e+04 1.876430e+04 1.882692e+04
mean abs. error 3.247212e+02 3.470205e+02 3.202556e+02 3.397084e+02
mean squared error 1.469184e+08 3.325902e+07 1.469328e+08 3.325471e+07
在本例中，兩種建模方法都產生了可比較的性能指標。由于實現原因，產品模型無法獲得解釋差異的百分比。
此外，我們還可以通過比較、觀察和預測測試和訓練子集的總索賠量來驗證這些模型。我們發現，平均而言，這兩種模型都傾向于低估總體索賠(但這種行為取決于正則化的數量)。
res = []
for subset_label, X, df in [
("train", X_train, df_train),
("test", X_test, df_test),
]:
exposure = df["Exposure"].values
res.append(
{
"subset": subset_label,
"observed": df["ClaimAmount"].values.sum(),
"predicted, frequency*severity model": np.sum(
exposure * glm_freq.predict(X) * glm_sev.predict(X)
),
"predicted, tweedie, power=%.2f"
% glm_pure_premium.power: np.sum(
exposure * glm_pure_premium.predict(X)),
}
)
print(pd.DataFrame(res).set_index("subset").T)
subset train test
observed 4.577616e+06 1.725665e+06
predicted, frequency*severity model 4.566477e+06 1.495871e+06
predicted, tweedie, power=1.90 4.451918e+06 1.432048e+06
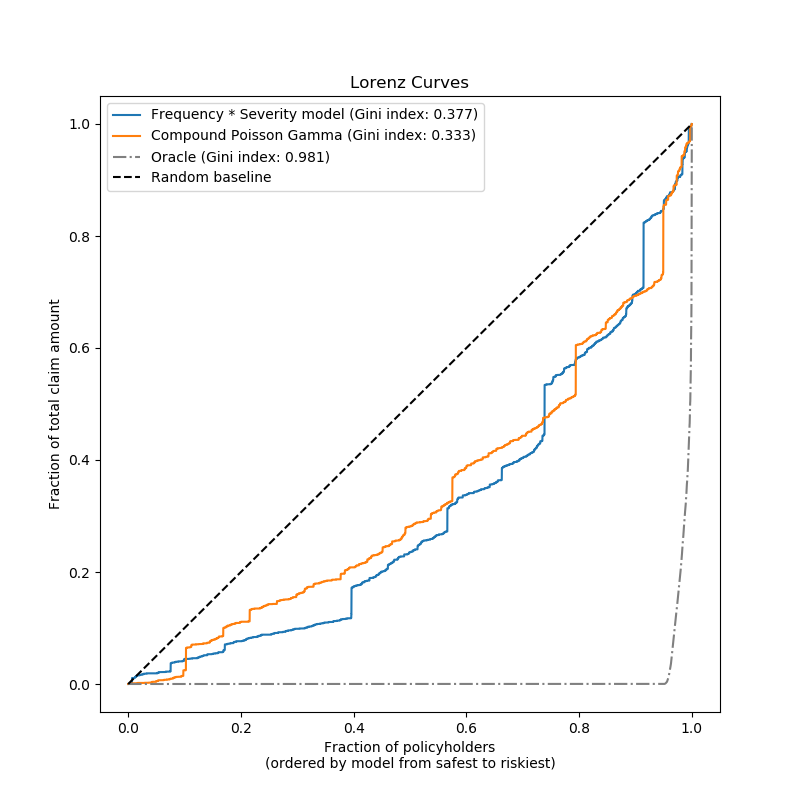
最后，我們可以用累索賠圖對這兩種模型進行比較：對于每個模型，投保人從最安全到最危險的等級，觀察到的累計索賠的比例繪制在y軸上。這個圖通常被稱為模型的有序Lorenz曲線。
基尼系數(基于曲線下面積)可以作為模型選擇指標，量化模型對投保人進行評級的能力。請注意，此指標并不反映模型根據索賠總額的絕對值作出準確預測的能力，而僅以相對金額作為排序指標。
這兩種模型都能夠按風險程度對投保人進行排序，但由于少量特征預測問題的自然難度較少，因此兩者都遠未完善。
請注意，GINI指數只表征模型的排名性能，而不是它的校準：預測的任何單調變換都會使模型的基尼指數保持不變。
最后，應該強調的是，直接適用于純保險費的復合Poisson Gamma模型在操作上更易于開發和維護，因為它包含在單個scikit-learn估計器中，而不是一對模型，每個模型都有自己的一組超參數。
def lorenz_curve(y_true, y_pred, exposure):
y_true, y_pred = np.asarray(y_true), np.asarray(y_pred)
exposure = np.asarray(exposure)
# order samples by increasing predicted risk:
ranking = np.argsort(y_pred)
ranked_exposure = exposure[ranking]
ranked_pure_premium = y_true[ranking]
cumulated_claim_amount = np.cumsum(ranked_pure_premium * ranked_exposure)
cumulated_claim_amount /= cumulated_claim_amount[-1]
cumulated_samples = np.linspace(0, 1, len(cumulated_claim_amount))
return cumulated_samples, cumulated_claim_amount
fig, ax = plt.subplots(figsize=(8, 8))
y_pred_product = glm_freq.predict(X_test) * glm_sev.predict(X_test)
y_pred_total = glm_pure_premium.predict(X_test)
for label, y_pred in [("Frequency * Severity model", y_pred_product),
("Compound Poisson Gamma", y_pred_total)]:
ordered_samples, cum_claims = lorenz_curve(
df_test["PurePremium"], y_pred, df_test["Exposure"])
gini = 1 - 2 * auc(ordered_samples, cum_claims)
label += " (Gini index: {:.3f})".format(gini)
ax.plot(ordered_samples, cum_claims, linestyle="-", label=label)
# Oracle model: y_pred == y_test
ordered_samples, cum_claims = lorenz_curve(
df_test["PurePremium"], df_test["PurePremium"], df_test["Exposure"])
gini = 1 - 2 * auc(ordered_samples, cum_claims)
label = "Oracle (Gini index: {:.3f})".format(gini)
ax.plot(ordered_samples, cum_claims, linestyle="-.", color="gray",
label=label)
# Random baseline
ax.plot([0, 1], [0, 1], linestyle="--", color="black",
label="Random baseline")
ax.set(
title="Lorenz Curves",
xlabel=('Fraction of policyholders\n'
'(ordered by model from safest to riskiest)'),
ylabel='Fraction of total claim amount'
)
ax.legend(loc="upper left")
plt.plot()
[]
腳本的總運行時間：(0分35.831秒)
Download Python source code:plot_tweedie_regression_insurance_claims.py
Download Jupyter notebook:plot_tweedie_regression_insurance_claims.ipynb