等滲回歸?

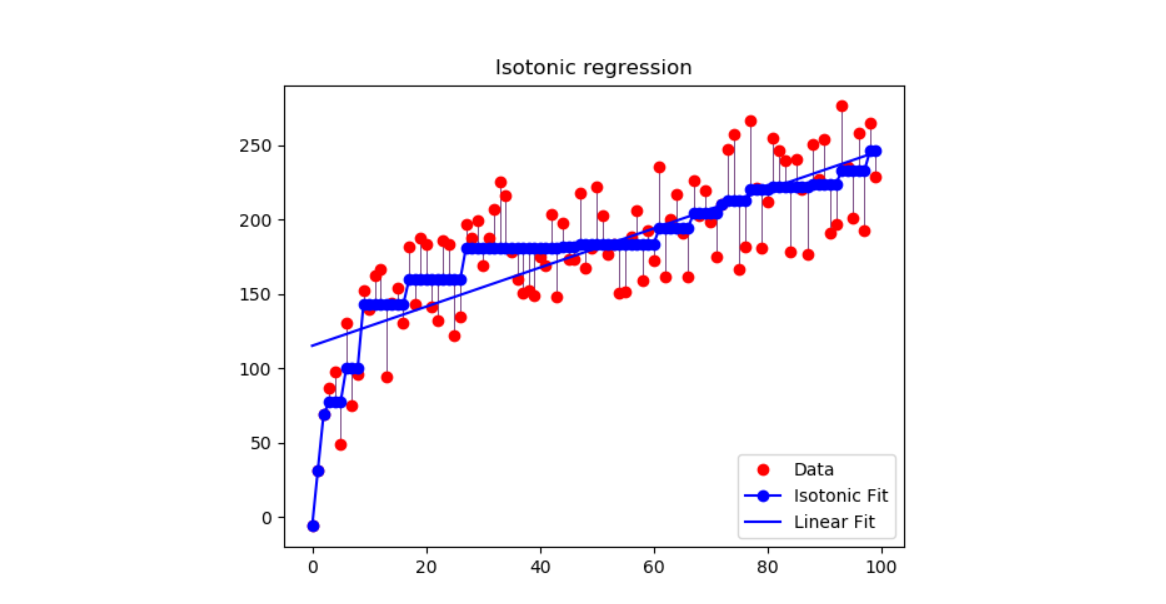
在生成的數據集上展示等身回歸的用法。等滲回歸會尋找函數的非遞減近似，同時使訓練數據的均方誤差最小。 這種模型的好處是它不會對目標函數采用任何形式的假設，例如線性。為了比較，還使用了線性回歸。

# 代碼作者: Nelle Varoquaux <nelle.varoquaux@gmail.com>
#          Alexandre Gramfort <alexandre.gramfort@inria.fr>
# 執照: BSD

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection

from sklearn.linear_model import LinearRegression
from sklearn.isotonic import IsotonicRegression
from sklearn.utils import check_random_state

n = 100
x = np.arange(n)
rs = check_random_state(0)
y = rs.randint(-50, 50, size=(n,)) + 50. * np.log1p(np.arange(n))

# #############################################################################
#擬合等滲回歸和線性回歸模型

ir = IsotonicRegression()

y_ = ir.fit_transform(x, y)

lr = LinearRegression()
lr.fit(x[:, np.newaxis], y)  #對線性回歸而言X需要時二維的

# #############################################################################
# 繪制結果

segments = [[[i, y[i]], [i, y_[i]]] for i in range(n)]
lc = LineCollection(segments, zorder=0)
lc.set_array(np.ones(len(y)))
lc.set_linewidths(np.full(n, 0.5))

fig = plt.figure()
plt.plot(x, y, 'r.', markersize=12)
plt.plot(x, y_, 'b.-', markersize=12)
plt.plot(x, lr.predict(x[:, np.newaxis]), 'b-')
plt.gca().add_collection(lc)
plt.legend(('Data', 'Isotonic Fit', 'Linear Fit'), loc='lower right')
plt.title('Isotonic regression')
plt.show()

輸出：

腳本的總運行時間：0分鐘0.124秒