繪制學習曲線?
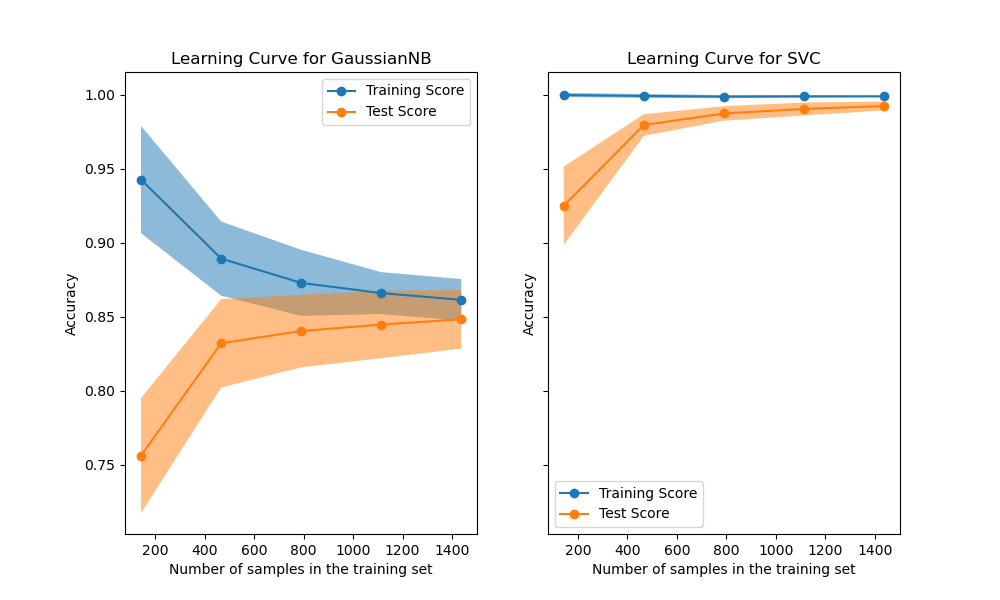
在第一列的第一行中,顯示了手寫數字數據集上樸素貝葉斯分類器的學習曲線。 請注意,訓練分數和交叉驗證分數最后都不太好。但是,這個曲線的形狀經常會在更復雜的數據集中被找到:訓練得分在開始時很高,然后降低,而交叉驗證得分在開始時很低但是之后增加。在第二列的第一行中,我們看到帶有RBF內核的SVM的學習曲線。我們可以清楚地看到,訓練分數仍在最大值附近,并且可以通過增加訓練樣本來增加驗證分數。第二行中的圖顯示了模型使用各種大小的訓練數據集進行訓練所需的時間。第三行中的圖顯示了每種訓練規模需要多少時間來訓練模型。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
def plot_learning_curve(estimator, title, X, y, axes=None, ylim=None, cv=None,
n_jobs=None, train_sizes=np.linspace(.1, 1.0, 5)):
"""
生成3個圖:測試和訓練學習曲線,訓練樣本與擬合時間曲線,擬合時間與得分曲線。
參數
----------
estimator : 實現“ fit”和“ predict”方法的對象類型
每次驗證都會克隆的該類型的對象。
title : 字符串
圖表標題。
X : 類數組,結構為(n_samples,n_features)
訓練向量,其中n_samples是樣本數,n_features是特征的數量。
y : 類數組,結構為(n_samples)或(n_samples,n_features),可選
相對于X的目標進行分類或回歸;
對于無監督學習,該參數沒有值。
axes : 3軸的數組,可選(默認=無)
用于繪制曲線的軸。
ylim : 元組,結構為(ymin,ymax),可選
定義繪制的最小和最大y值。
cv : 整數型, 交叉驗證生成器或一個可迭代對象,可選
確定交叉驗證拆分策略。
可能的輸入是:
- 無(None),使用默認的5折交叉驗證,
- 整數,用于指定折數。
- 交叉驗證分割器,詳見下文
- 可迭代的數據(訓練,測試)拆分成的索引數組
對于整數或/None輸入, 如果y是二分類或多分類,則使用StratifiedKFold作為交叉驗證分割器。如果估算器不是分類類型或標簽y不是二分類uo多分類,則使用KFold作為交叉驗證分割器。
引用:有關可以在此處使用的交叉驗證器的各種信息,請參見用戶指南<cross_validation>
n_jobs : 整數或None, 可選(默認是None)
要并行運行的作業數。
除非在obj:`joblib.parallel_backend`上下文中,否則“ None``表示1。-1表示使用所有處理器。有關更多詳細信息,請參見術語<n_jobs>`。
train_sizes : 類數組, 結構為 (n_ticks,), 浮點數或整數
訓練示例的相對或絕對數量,將用于生成學習曲線。如果數據類型為浮點數,則將其視為訓練集最大大小的一部分(由所選驗證方法確定),即,它必須在(0,1]之內。否則,則將其解釋為訓練集的絕對大小。
請注意,為了進行分類,樣本數量通常必須足夠大,以包含每個類別中的至少一個樣本。(默認值:np.linspace(0.1, 1.0, 5))
"""
if axes is None:
_, axes = plt.subplots(1, 3, figsize=(20, 5))
axes[0].set_title(title)
if ylim is not None:
axes[0].set_ylim(*ylim)
axes[0].set_xlabel("Training examples")
axes[0].set_ylabel("Score")
train_sizes, train_scores, test_scores, fit_times, _ = \
learning_curve(estimator, X, y, cv=cv, n_jobs=n_jobs,
train_sizes=train_sizes,
return_times=True)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
fit_times_mean = np.mean(fit_times, axis=1)
fit_times_std = np.std(fit_times, axis=1)
# 繪制學習曲線
axes[0].grid()
axes[0].fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
axes[0].fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1,
color="g")
axes[0].plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
axes[0].plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
axes[0].legend(loc="best")
# Plot n_samples vs fit_times
axes[1].grid()
axes[1].plot(train_sizes, fit_times_mean, 'o-')
axes[1].fill_between(train_sizes, fit_times_mean - fit_times_std,
fit_times_mean + fit_times_std, alpha=0.1)
axes[1].set_xlabel("Training examples")
axes[1].set_ylabel("fit_times")
axes[1].set_title("Scalability of the model")
# 繪制擬合時間與得分
axes[2].grid()
axes[2].plot(fit_times_mean, test_scores_mean, 'o-')
axes[2].fill_between(fit_times_mean, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1)
axes[2].set_xlabel("fit_times")
axes[2].set_ylabel("Score")
axes[2].set_title("Performance of the model")
return plt
fig, axes = plt.subplots(3, 2, figsize=(10, 15))
X, y = load_digits(return_X_y=True)
title = "Learning Curves (Naive Bayes)"
# 進行100次迭代交叉驗證,以獲得更平滑的平均測試和訓練成績曲線,每次將20%的數據隨機選擇為驗證集。
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, axes=axes[:, 0], ylim=(0.7, 1.01),
cv=cv, n_jobs=4)
title = r"Learning Curves (SVM, RBF kernel, $\gamma=0.001$)"
# SVC的訓練代價比較昂貴,因此我們進行的CV迭代次數較少:
cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, axes=axes[:, 1], ylim=(0.7, 1.01),
cv=cv, n_jobs=4)
plt.show()
腳本的總運行時間:(0分鐘 4.601秒)
