特征離散化?
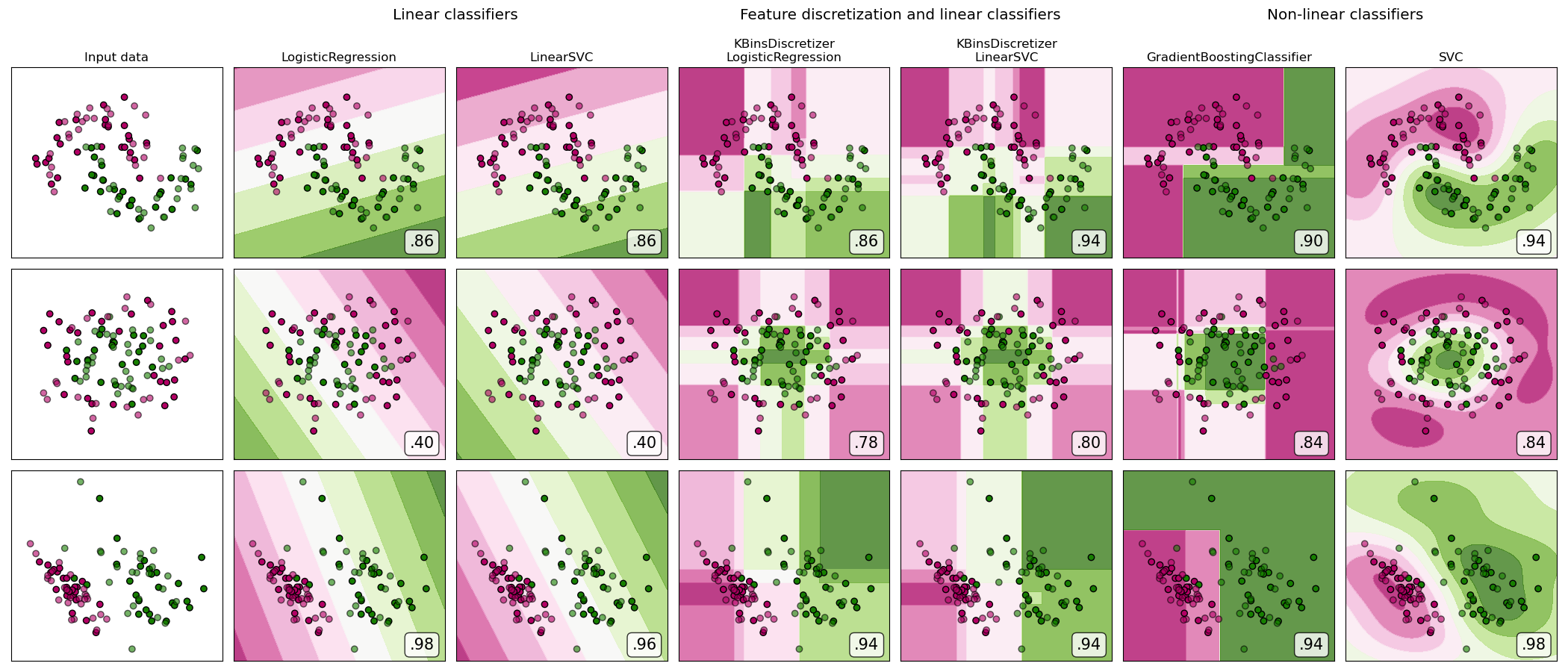
在合成分類數據集上進行特征離散化的演示。特征離散化將每個特征分解為一組bin,此處的寬度均勻分布。然后將離散值進行一次熱編碼,并提供給線性分類器。即使分類器是線性的,此預處理也可以實現非線性行為。
在此示例中,前兩行代表線性不可分離的數據集(月亮和同心圓),而第三行則近似線性可分離。在兩個線性不可分離的數據集上,特征離散化大大提高了線性分類器的性能。在線性可分離數據集上,特征離散化會降低線性分類器的性能。還顯示了兩個非線性分類器以進行比較。
此示例應以一粒鹽為準,因為傳達的直覺不一定會延續到實際數據集中。特別是在高維空間中,可以更輕松地線性分離數據。此外,使用特征離散化和一鍵編碼增加了特征數量,當樣本數量少時,容易導致過度擬合。
這些圖以純色顯示訓練點,測試點是半透明的。右下方顯示了測試集上的分類準確性。
# 源代碼: Tom Dupré la Tour
# 改編自Ga?l Varoquaux和Andreas Müller的plot_classifier_comparison
#
# 執照: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_moons, make_circles, make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.utils._testing import ignore_warnings
from sklearn.exceptions import ConvergenceWarning
print(__doc__)
h = .02 # 設置網格的補不長
def get_name(estimator):
name = estimator.__class__.__name__
if name == 'Pipeline':
name = [get_name(est[1]) for est in estimator.steps]
name = ' + '.join(name)
return name
# (estimator,param_grid)的列表,其中在GridSearchCV中使用param_grid
classifiers = [
(LogisticRegression(random_state=0), {
'C': np.logspace(-2, 7, 10)
}),
(LinearSVC(random_state=0), {
'C': np.logspace(-2, 7, 10)
}),
(make_pipeline(
KBinsDiscretizer(encode='onehot'),
LogisticRegression(random_state=0)), {
'kbinsdiscretizer__n_bins': np.arange(2, 10),
'logisticregression__C': np.logspace(-2, 7, 10),
}),
(make_pipeline(
KBinsDiscretizer(encode='onehot'), LinearSVC(random_state=0)), {
'kbinsdiscretizer__n_bins': np.arange(2, 10),
'linearsvc__C': np.logspace(-2, 7, 10),
}),
(GradientBoostingClassifier(n_estimators=50, random_state=0), {
'learning_rate': np.logspace(-4, 0, 10)
}),
(SVC(random_state=0), {
'C': np.logspace(-2, 7, 10)
}),
]
names = [get_name(e) for e, g in classifiers]
n_samples = 100
datasets = [
make_moons(n_samples=n_samples, noise=0.2, random_state=0),
make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
make_classification(n_samples=n_samples, n_features=2, n_redundant=0,
n_informative=2, random_state=2,
n_clusters_per_class=1)
]
fig, axes = plt.subplots(nrows=len(datasets), ncols=len(classifiers) + 1,
figsize=(21, 9))
cm = plt.cm.PiYG
cm_bright = ListedColormap(['#b30065', '#178000'])
# 在數據集上迭代
for ds_cnt, (X, y) in enumerate(datasets):
print('\ndataset %d\n---------' % ds_cnt)
# 預處理數據集,分為訓練和測試部分
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=.5, random_state=42)
# 為背景顏色創建網格
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(
np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# 首先繪制數據集
ax = axes[ds_cnt, 0]
if ds_cnt == 0:
ax.set_title("Input data")
# plot the training points
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright,
edgecolors='k')
# and testing points
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6,
edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
# 在分類器上迭代
for est_idx, (name, (estimator, param_grid)) in \
enumerate(zip(names, classifiers)):
ax = axes[ds_cnt, est_idx + 1]
clf = GridSearchCV(estimator=estimator, param_grid=param_grid)
with ignore_warnings(category=ConvergenceWarning):
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
print('%s: %.2f' % (name, score))
# 繪制決策邊界。
# 我們將為網格[x_min,x_max] * [y_min,y_max]中的每個點分配顏色。
if hasattr(clf, "decision_function"):
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
else:
Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
# 將結果放入顏色圖
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, cmap=cm, alpha=.8)
# 繪制訓練點
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright,
edgecolors='k')
# 以及測試點
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright,
edgecolors='k', alpha=0.6)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xticks(())
ax.set_yticks(())
if ds_cnt == 0:
ax.set_title(name.replace(' + ', '\n'))
ax.text(0.95, 0.06, ('%.2f' % score).lstrip('0'), size=15,
bbox=dict(boxstyle='round', alpha=0.8, facecolor='white'),
transform=ax.transAxes, horizontalalignment='right')
plt.tight_layout()
# 在圖像上增加標題
plt.subplots_adjust(top=0.90)
suptitles = [
'Linear classifiers',
'Feature discretization and linear classifiers',
'Non-linear classifiers',
]
for i, suptitle in zip([1, 3, 5], suptitles):
ax = axes[0, i]
ax.text(1.05, 1.25, suptitle, transform=ax.transAxes,
horizontalalignment='center', size='x-large')
plt.show()
輸出:
dataset 0
---------
LogisticRegression: 0.86
LinearSVC: 0.86
KBinsDiscretizer + LogisticRegression: 0.86
KBinsDiscretizer + LinearSVC: 0.92
GradientBoostingClassifier: 0.90
SVC: 0.94
dataset 1
---------
LogisticRegression: 0.40
LinearSVC: 0.40
KBinsDiscretizer + LogisticRegression: 0.88
KBinsDiscretizer + LinearSVC: 0.86
GradientBoostingClassifier: 0.80
SVC: 0.84
dataset 2
---------
LogisticRegression: 0.98
LinearSVC: 0.98
KBinsDiscretizer + LogisticRegression: 0.94
KBinsDiscretizer + LinearSVC: 0.94
GradientBoostingClassifier: 0.88
SVC: 0.98
腳本的總運行時間:(0分鐘25.699秒)
