處理平局的支持向量機?

（譯者注：支持向量機依靠決策邊界來進行分類，當一個點更靠近某條決策邊界，這個點就更可能被分到這個決策邊界所代表的那一類。但會存在一些點，位于邊際的中間，即到兩個決策邊界的距離是一致的，此時這個點的狀況就會被叫做“平局”）

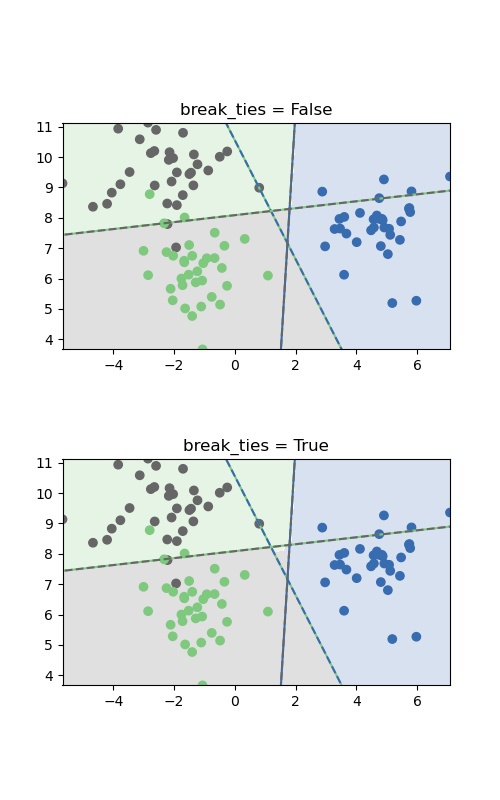
如果decision_function_shape的值是'ovr'，則打破平局的計算代價是高的，因此默認情況下不啟用ovr選項。此示例說明了break_ties參數對多類分類問題和Decision_function_shape ='ovr'的影響。

這兩個圖像的區別僅在于類別被綁在一起的中間區域。如果break_ties = False，則該區域中的所有輸入將歸為一類，而如果break_ties = True，則平局決勝機制將在該區域中創建非凸決策邊界。

輸入：

print(__doc__)

# 代碼來源: Andreas Mueller, Adrin Jalali
# 執照: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_blobs

X, y = make_blobs(random_state=27)

fig, sub = plt.subplots(2, 1, figsize=(5, 8))
titles = ("break_ties = False",
          "break_ties = True")

for break_ties, title, ax in zip((False, True), titles, sub.flatten()):

    svm = SVC(kernel="linear", C=1, break_ties=break_ties,
              decision_function_shape='ovr').fit(X, y)

    xlim = [X[:, 0].min(), X[:, 0].max()]
    ylim = [X[:, 1].min(), X[:, 1].max()]

    xs = np.linspace(xlim[0], xlim[1], 1000)
    ys = np.linspace(ylim[0], ylim[1], 1000)
    xx, yy = np.meshgrid(xs, ys)

    pred = svm.predict(np.c_[xx.ravel(), yy.ravel()])

    colors = [plt.cm.Accent(i) for i in [0, 4, 7]]

    points = ax.scatter(X[:, 0], X[:, 1], c=y, cmap="Accent")
    classes = [(0, 1), (0, 2), (1, 2)]
    line = np.linspace(X[:, 1].min() - 5, X[:, 1].max() + 5)
    ax.imshow(-pred.reshape(xx.shape), cmap="Accent", alpha=.2,
              extent=(xlim[0], xlim[1], ylim[1], ylim[0]))

    for coef, intercept, col in zip(svm.coef_, svm.intercept_, classes):
        line2 = -(line * coef[1] + intercept) / coef[0]
        ax.plot(line2, line, "-", c=colors[col[0]])
        ax.plot(line2, line, "--", c=colors[col[1]])
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)
    ax.set_title(title)
    ax.set_aspect("equal")

plt.show()

腳本的總運行時間：（0分鐘1.077秒）