三分類的概率校準?
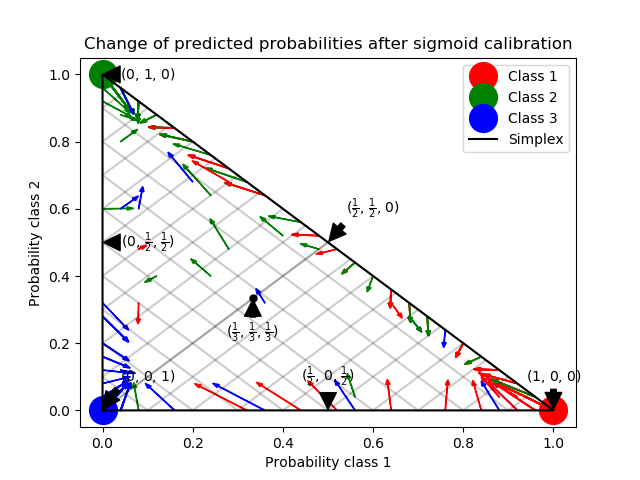
此示例說明了sigmoid如何校準三分類問題預測的概率。舉例說明的是標準的2-simplex,其中三個角對應于三個類。箭頭指向由未校準分類器預測的概率向量到同一分類器在hold-out 驗證集上進行sigmoid校準后預測的概率向量。顏色表示實例的真正類(紅色:1類,綠色:2類,藍色:3類)。
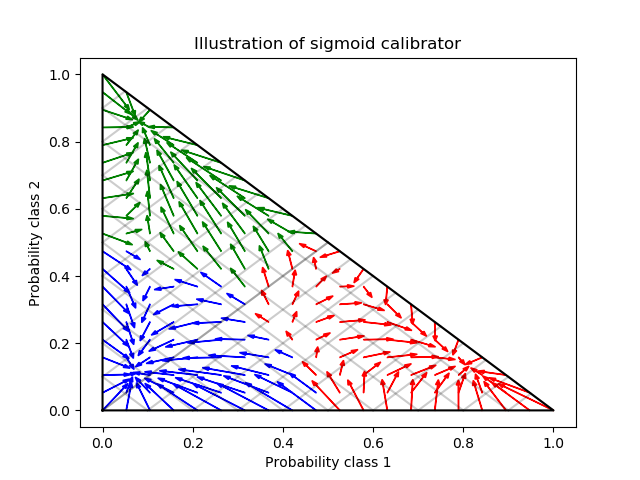
基分類器是具有25個基估計器(樹)的隨機林分類器。如果這個分類器對所有800個訓練數據點都進行了訓練,那么它對它的預測過于自信,從而導致大量的日志丟失。校準一個相同的分類器, 這個分類器在600個數據點上被訓練, 在其余的200個數據點上用 method=’sigmoid’降低了預測的可信度。即, 將概率向量從simplex的邊緣, 移動到中心。這種校準導致較低的對數損失。既然這種替代選擇不得不增加基估計器 的數量, 這將導致類似的對數損失(log-loss)。
Log-loss of
* uncalibrated classifier trained on 800 datapoints: 1.280
* classifier trained on 600 datapoints and calibrated on 200 datapoint: 0.534
print(__doc__)
# Author: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
# License: BSD Style.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
from sklearn.calibration import CalibratedClassifierCV
from sklearn.metrics import log_loss
np.random.seed(0)
# Generate data
X, y = make_blobs(n_samples=1000, random_state=42, cluster_std=5.0)
X_train, y_train = X[:600], y[:600]
X_valid, y_valid = X[600:800], y[600:800]
X_train_valid, y_train_valid = X[:800], y[:800]
X_test, y_test = X[800:], y[800:]
# Train uncalibrated random forest classifier on whole train and validation
# data and evaluate on test data
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train_valid, y_train_valid)
clf_probs = clf.predict_proba(X_test)
score = log_loss(y_test, clf_probs)
# Train random forest classifier, calibrate on validation data and evaluate
# on test data
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train, y_train)
clf_probs = clf.predict_proba(X_test)
sig_clf = CalibratedClassifierCV(clf, method="sigmoid", cv="prefit")
sig_clf.fit(X_valid, y_valid)
sig_clf_probs = sig_clf.predict_proba(X_test)
sig_score = log_loss(y_test, sig_clf_probs)
# Plot changes in predicted probabilities via arrows
plt.figure()
colors = ["r", "g", "b"]
for i in range(clf_probs.shape[0]):
plt.arrow(clf_probs[i, 0], clf_probs[i, 1],
sig_clf_probs[i, 0] - clf_probs[i, 0],
sig_clf_probs[i, 1] - clf_probs[i, 1],
color=colors[y_test[i]], head_width=1e-2)
# Plot perfect predictions
plt.plot([1.0], [0.0], 'ro', ms=20, label="Class 1")
plt.plot([0.0], [1.0], 'go', ms=20, label="Class 2")
plt.plot([0.0], [0.0], 'bo', ms=20, label="Class 3")
# Plot boundaries of unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], 'k', label="Simplex")
# Annotate points on the simplex
plt.annotate(r'($\frac{1}{3}$, $\frac{1}{3}$, $\frac{1}{3}$)',
xy=(1.0/3, 1.0/3), xytext=(1.0/3, .23), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.plot([1.0/3], [1.0/3], 'ko', ms=5)
plt.annotate(r'($\frac{1}{2}$, $0$, $\frac{1}{2}$)',
xy=(.5, .0), xytext=(.5, .1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($0$, $\frac{1}{2}$, $\frac{1}{2}$)',
xy=(.0, .5), xytext=(.1, .5), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($\frac{1}{2}$, $\frac{1}{2}$, $0$)',
xy=(.5, .5), xytext=(.6, .6), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($0$, $0$, $1$)',
xy=(0, 0), xytext=(.1, .1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($1$, $0$, $0$)',
xy=(1, 0), xytext=(1, .1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
plt.annotate(r'($0$, $1$, $0$)',
xy=(0, 1), xytext=(.1, 1), xycoords='data',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='center', verticalalignment='center')
# Add grid
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], 'k', alpha=0.2)
plt.plot([0, 0 + (1-x)/2], [x, x + (1-x)/2], 'k', alpha=0.2)
plt.plot([x, x + (1-x)/2], [0, 0 + (1-x)/2], 'k', alpha=0.2)
plt.title("Change of predicted probabilities after sigmoid calibration")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.legend(loc="best")
print("Log-loss of")
print(" * uncalibrated classifier trained on 800 datapoints: %.3f "
% score)
print(" * classifier trained on 600 datapoints and calibrated on "
"200 datapoint: %.3f" % sig_score)
# Illustrate calibrator
plt.figure()
# generate grid over 2-simplex
p1d = np.linspace(0, 1, 20)
p0, p1 = np.meshgrid(p1d, p1d)
p2 = 1 - p0 - p1
p = np.c_[p0.ravel(), p1.ravel(), p2.ravel()]
p = p[p[:, 2] >= 0]
calibrated_classifier = sig_clf.calibrated_classifiers_[0]
prediction = np.vstack([calibrator.predict(this_p)
for calibrator, this_p in
zip(calibrated_classifier.calibrators_, p.T)]).T
prediction /= prediction.sum(axis=1)[:, None]
# Plot modifications of calibrator
for i in range(prediction.shape[0]):
plt.arrow(p[i, 0], p[i, 1],
prediction[i, 0] - p[i, 0], prediction[i, 1] - p[i, 1],
head_width=1e-2, color=colors[np.argmax(p[i])])
# Plot boundaries of unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], 'k', label="Simplex")
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], 'k', alpha=0.2)
plt.plot([0, 0 + (1-x)/2], [x, x + (1-x)/2], 'k', alpha=0.2)
plt.plot([x, x + (1-x)/2], [0, 0 + (1-x)/2], 'k', alpha=0.2)
plt.title("Illustration of sigmoid calibrator")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.show()
腳本的總運行時間:(0分0.814秒)
