1.3 內核嶺回歸?

內核嶺回歸(Kernel ridge regression (KRR)) [M2012] , 是組合使用了內核技巧和嶺回歸(進行了l2正則化的最小二乘法)。因此，它所學習到的在空間中不同的線性函數是由不同的內核和數據所導致的。對于非線性的內核，它與原始空間中的非線性函數相對應。

通過 KernelRidge學習到的模型與支持向量回歸（SVR）是一樣的。但是他們使用了不同的損失函數：內核嶺回歸(KRR)使用了均方誤差損失(squared error loss), 而支持向量回歸(support vector regression， SVR)使用了 -insensitive損失， 兩則都使用了l2進行正則化。與[`SVR`](http://www.ipahlj.com/view/782.html)相反， [`KernelRidge`](http://www.ipahlj.com/view/377.html) 的擬合可以以封閉形式進行，而且對于中等大小的數據集來說通常更快。在另一方面， 它所學習的模型是非稀疏的，因此在預測時間上來看比支持向量回歸(SVR)要慢, 而支持向量回歸對于會學習一個稀疏的模型。

下圖比較了人造數據集上的KernelRidge和 SVR，這是一個包含正弦函數和每五個數據點就加上一個強噪聲的數據集。下面繪制了 KernelRidge和SVR的模型， 通過網格搜索優化了（高斯**）**徑向基函數核函數（RBF核）的復雜度、正則化和帶寬。學習的函數是非常相似的；然而，都是網格搜索情況下， 擬合KernelRidge大約比擬合SVR快7倍。然而，100000目標值的預測要快三倍多，因為它已經學習了一個稀疏模型，僅使用100個訓練數據點的1/3作為支持向量。

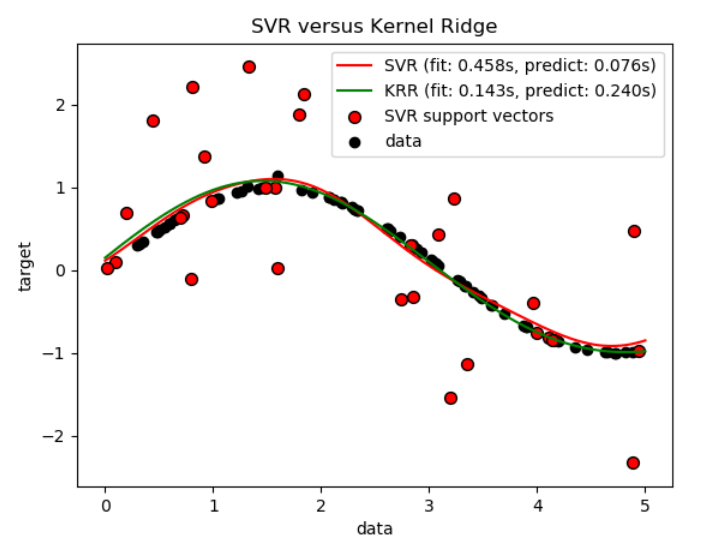下一個圖比較了在不同大小的訓練集上KernelRidge和SVR的擬合和預測時間。對于中等訓練集，擬合KernelRidge比 SVR快(小于1000個樣本)；然而，對于更大的訓練集，SVR通常更好。關于預測的時間，在所有大小的訓練集上SVR比KernelRidge更快，因為學習SVR得到的是稀疏的解。請注意，稀疏的程度和預測的時間取決于SVR的參數?和C；?=0將對應于稠密模型。

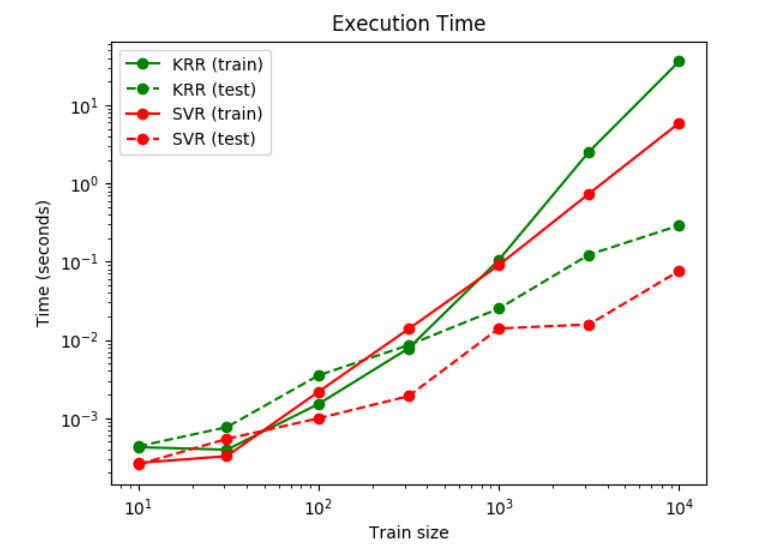
參考

[2012]"機器學習：概率視角"Murphy, K. P. - chapter 14.4.3, pp. 492-493, The MIT Press, 2012