sklearn.gaussian_process.RBF?
class sklearn.gaussian_process.kernels.RBF(length_scale=1.0, length_scale_bounds=(1e-05, 100000.0))
徑向基函數核(又稱平方指數核)。
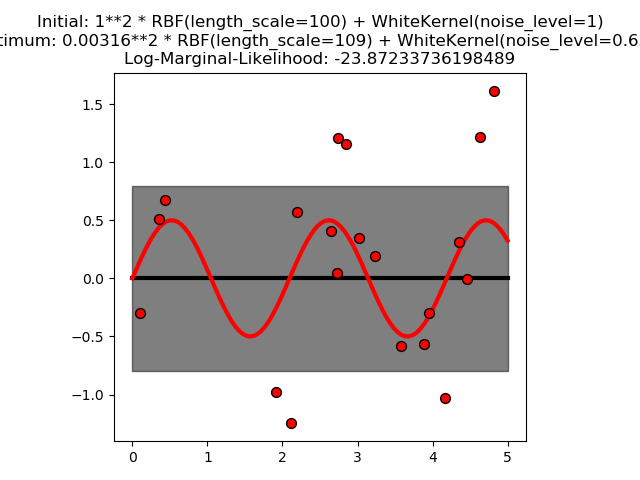
RBF核是一個平穩核。它也被稱為“平方指數”核。它由一個長度尺度參數參數化,該參數可以是標量(核函數的各向同性變量),也可以是與輸入X具有相同維數的向量(核函數的各向異性變量)。核函數為:
其中核的長度尺度,為歐氏距離。有關如何設置長度刻度參數的建議,請參見[1]。
這個核是無限可微的,這意味著以這個核為協方差函數的GPs具有所有階的均方導數,因此非常平滑。有關RBF內核的更多細節,請參閱[2],第4章,第4.2節。
在用戶指南中閱讀更多內容。
新版本 0.18 。
| 參數 | 說明 |
|---|---|
| length_scale | loat or ndarray of shape (n_features,), default=1.0 核的長度尺度。如果是浮點數,則使用各向同性核。如果是一個數組,則使用各向異性核,其中l的每個維數定義了各自特征維數的長度尺度。 |
| length_scale_bounds | pair of floats >= 0 or “fixed”, default=(1e-5, 1e5) length_scale上的下界和上界。如果設置為“固定”,則“length_scale”在超參數調優期間無法更改。 |
| 屬性 | 說明 |
|---|---|
| anisotropic | |
| bounds | 返回的對數變換界限。 |
| hyperparameter_length_scale | |
| hyperparameters | 返回所有超參數規范的列表。 |
| n_dims | 返回內核的非固定超參數的數量。 |
| requires_vector_input | 返回內核是在固定長度的特征向量上定義的還是在通用對象上定義的。 |
| theta | 返回(扁平的、對數轉換的)非固定超參數。 |
參考文獻
1David Duvenaud (2014). “The Kernel Cookbook: Advice on Covariance functions”. 2Carl Edward Rasmussen, Christopher K. I. Williams (2006). “Gaussian Processes for Machine Learning”. The MIT Press.
示例
>>> from sklearn.datasets import load_iris
>>> from sklearn.gaussian_process import GaussianProcessClassifier
>>> from sklearn.gaussian_process.kernels import RBF
>>> X, y = load_iris(return_X_y=True)
>>> kernel = 1.0 * RBF(1.0)
>>> gpc = GaussianProcessClassifier(kernel=kernel,
... random_state=0).fit(X, y)
>>> gpc.score(X, y)
0.9866...
>>> gpc.predict_proba(X[:2,:])
array([[0.8354..., 0.03228..., 0.1322...],
[0.7906..., 0.0652..., 0.1441...]])
方法
| 方法 | 說明 |
|---|---|
__call__(self, X[, Y, eval_gradient]) |
返回核函數k(X, Y)和它的梯度。 |
clone_with_theta(self, theta) |
返回帶有給定超參數theta的self的克隆。 |
diag(self, X) |
返回核函數k(X, X)的對角線。 |
get_params(self[, deep]) |
獲取這個內核的參數。 |
is_stationary(self) |
返回內核是否靜止。 |
set_params(self, **params) |
設置這個內核的參數。 |
__init__(self, length_scale=1.0, length_scale_bounds=(1e-05, 100000.0))
初始化self. 請參閱help(type(self))以獲得準確的說明 。
__call__(self, X, Y=None, eval_gradient=False)
返回核函數k(X, Y)和它的梯度。
| 參數 | 說明 |
|---|---|
| X | ndarray of shape (n_samples_X, n_features) 返回核函數k(X, Y)的左參數 |
| Y | ndarray of shape (n_samples_Y, n_features), default=None 返回的核函數k(X, Y)的正確參數。如果沒有,則計算k(X, X)。 |
| eval_gradient | bool, default=False 確定關于核超參數的梯度是否確定。只有當Y沒有的時候才被支持。 |
| 返回值 | 說明 |
|---|---|
| K | ndarray of shape (n_samples_X, n_samples_Y) 內核k (X, Y) |
| K_gradient | ndarray of shape (n_samples_X, n_samples_X, n_dims), optional 核函數k(X, X)關于核函數超參數的梯度。只有當 eval_gradient為真時才返回。 |
property bounds
返回的對數變換界限。
| 返回值 | 說明 |
|---|---|
| bounds | ndarray of shape (n_dims, 2) 核函數超參數的對數變換界限 |
clone_with_theta(self, theta)
返回帶有給定超參數theta的self的克隆。
| 參數 | 說明 |
|---|---|
| theta | ndarray of shape (n_dims,) 的hyperparameters |
diag(self, X)
返回核函數k(X, X)的對角線。
該方法的結果與np.diag(self(X))相同;但是,由于只計算對角,因此可以更有效地計算它。
| 參數 | 說明 |
|---|---|
| X | ndarray of shape (n_samples_X, n_features) 返回核函數k(X, Y)的左參數 |
| 返回值 | 說明 |
|---|---|
| K_diag | ndarray of shape (n_samples_X,) 核k(X, X)的對角線 |
get_params(self, deep=True)
獲取這個內核的參數。
| 參數 | 說明 |
|---|---|
| deep | bool, default=True 如果為真,將返回此估計器的參數以及包含的作為估計器的子對象。 |
| 返回值 | 說明 |
|---|---|
| params | dict 參數名稱映射到它們的值。 |
property hyperparameters
返回所有超參數的列表。
is_stationary(self)
返回內核是否靜止。
property n_dims
返回內核的非固定超參數的數量。
property requires_vector_input
返回內核是在固定長度的特征向量上定義的還是在通用對象上定義的。向后兼容性的默認值為True。
set_params(self, **params)
設置這個內核的參數。
該方法適用于簡單估計量和嵌套對象(如pipline)。后者具有形式為<component>_<parameter>的參數,這樣就讓更新嵌套對象的每個組件成為了可能。
| 返回值 | 說明 |
|---|---|
| self | 無 |
property theta
返回(扁平的、對數轉換的)非固定超參數。
注意,theta通常是內核超參數的對數變換值,因為這種搜索空間的表示更適合超參數搜索,因為像長度尺度這樣的超參數自然存在于對數尺度上。
| 返回值 | 說明 |
|---|---|
| theta | ndarray of shape (n_dims,) 核函數的非固定、對數變換超參數 |