2.4. 雙聚類?

可以使用sklearn.cluster.bicluster模塊進行Biclustering(雙聚類) 。 雙聚類算法同時對數據矩陣的行和列進行聚類。而這些行列的聚類稱之為雙向簇(biclusters)。每一次聚類都會基于原始數據矩陣確定一個子矩陣, 并且這些子矩陣具有一些需要的屬性。

例如, 給定一個矩陣 (10, 10) 的矩陣 , 如果對其中 3 行 2 列進行雙向聚類，就可以誘導出一個子矩陣 (3, 2)。

>>> import numpy as np
>>> data = np.arange(100).reshape(10, 10)
>>> rows = np.array([0, 2, 3])[:, np.newaxis]
>>> columns = np.array([1, 2])
>>> data[rows, columns]
array([[ 1,  2],
       [21, 22],
       [31, 32]])

出于可視化目的，給定一個雙向簇，可以重新排列數據矩陣的行和列以使雙向簇是連續的。

不同的雙向聚類算法在如何定義雙向簇方面有所不同，一些常見的類型包括：

  • 常量, 常量行或常量列
  • 異常高或低的值
  • 低方差的子矩陣
  • 相關聯的行或列

算法采用不同的方式給雙向簇分配行列，這導致了不同的雙向聚類結構。當將行和列劃分為區塊時，將出現塊對角或棋盤結構。

如果每一行和每一列恰好屬于一個二元組，則重新排列數據矩陣的行和列將顯示對角線上的二元組。這是此結構的示例，此結構的雙向簇具有比其他行列更高的平均值:

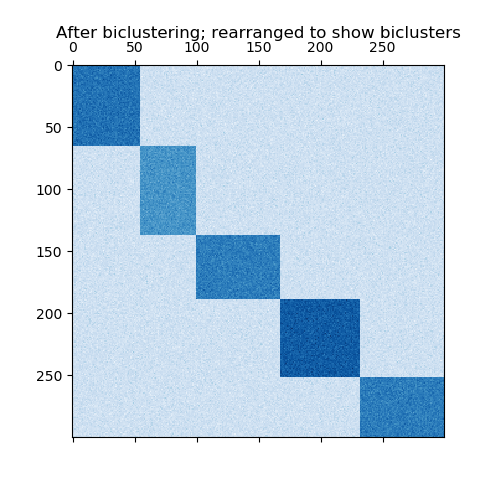? 通過分隔行和列形成的雙向簇的示例

在棋盤結構的例子中，每一行屬于所有的列簇, 每一列屬于所有的行簇。下面是這種結構的一個例子，每個雙向簇內的值差異較小:

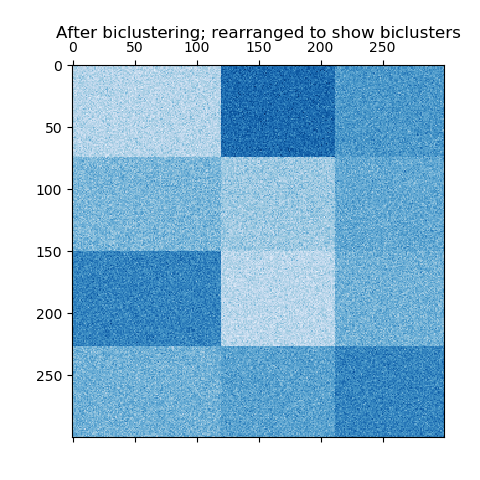? 棋盤格狀雙簇的示例

在對模型進行擬合之后，可以在 rows_ 和 columns_ 屬性中找到行簇和列簇的歸屬信息。rows_[i] 是一個二元向量，其中非零項對應于屬于雙向簇i 的行。 columns_[i] 就表示屬于雙向簇 i 的列。

一些模型還具有 row_labels_ 和 column_labels_ 屬性。這些模型劃分行和列，例如在塊對角或者棋盤雙向簇結構。

注意 雙向聚類在不同的領域有很多其他名稱，包括 co-clustering, two-mode clustering, two-way clustering, block clustering, coupled two-way clustering 等等。一些算法的名稱，比如 Spectral Co-Clustering algorithm, 反映了這些替代名稱。

2.4.1. 聯合譜聚類

SpectralCoclustering(聯合譜聚類)算法可以找到比對應的其他行和列的值更高的雙向簇（biclusters）。每一行和每一列都只對應一個雙向簇, 因此重新分配行和列以使分區相鄰，顯示對角線上的高值:

注意：該算法將輸入數據矩陣看做成二分圖：矩陣的行和列對應于兩組頂點，每個條目對應于行和列之間的一條邊，該算法近似于此圖的歸一化割，以找到重子圖。

2.4.1.1. 數學公式

可以 通常這意味著直接使用拉普拉斯矩陣。 如果原始數據矩陣 的形狀為 , 則對應的二分圖的拉普拉斯矩陣具有形狀 (m+n)×(m+n)。 但是, 在這種情況下, 直接使用 , 因為它更小，更有效。

輸入矩陣 預處理如下：

為對角線矩陣，其中元素 等于 ， 是對角矩陣，其中 等于 ，

奇異值分解, 產生了 行列的分區，左邊奇異向量的子集給予行分區，右邊的奇異向量的子集給予列分區。

奇異向量 從第二個開始，奇異向量提供了所需的分區信息，它們用于形成矩陣 ：

的列是 類似于 。 然后 的所有行通過k-means進行聚類. 第一個n_rows 標簽提供行分區信息, 剩下的 n_columns 標簽提供列分區信息。

示例:

參考文獻:

2.4.2. 光譜雙聚類

該SpectralBiclustering算法假定輸入數據矩陣具有隱藏的棋盤結構。可以對具有這種結構的矩陣的行和列進行分區，例如，如果有兩個行分區和三個列分區，則每行將屬于三個bicluster，而每列將屬于兩個bicluster。

該算法對矩陣的行和列進行劃分，以使相應的塊狀不變的棋盤矩陣可以很好地逼近原始矩陣。

2.4.2.1. 數學表示

先歸一化輸入矩陣 ，使得矩陣的棋盤模式更明顯。有三種可能的方法:

  1. 獨立的行列歸一化，如聯合譜聚類中所示。此方法使行總和為常量，而列總和為另一個的常量。
  2. Bistochastization: 重復行和列歸一化直到收斂。此方法使行和列的總和為相同的常數。
  3. 對數歸一化: 計算數據矩陣的對數 。列均值是 ，行均值是 ，是 的整體平均。根據公式計算出最終矩陣：

歸一化之后，就像在聯合譜聚類算法中一樣，計算前幾個奇異矢量。

如果使用對數歸一化，則所有奇異向量都是有意義的。但是, 如果使用獨立的歸一化或雙歧化, 則第一個奇異矢量 和 被丟棄。從現在開始，“第一個“奇異向量指的是 和 對數歸一化的情況除外。

給定這些奇異向量，按照分段常數向量的最佳近似程度進行排序。使用一維 k-means 找到每個向量的近似值，并使用歐氏距離進行評分。選擇最佳左右奇異向量的一些子集。接下來, 將數據投影到奇異向量的最佳子集并進行聚類。

例如，如果計算 個奇異向量，因為 $q

示例:

參考資料:

2.4.3. Biclustering 評價

評估雙聚類結果有兩種方法：內部和外部。內部度量,如聚類穩定性, 只依賴于數據和結果本身。目前scikit-learn還沒有內部的雙向簇度量。外部度量是指外部信息來源，例如真實解。當處理真實數據時，真實解通常是未知的，但是，雙聚類人工數據可能有助于精確地評估算法，因為真實解是已知的。

為了將一組已發現的雙向簇與一組真實的雙向簇行比較，需要兩種相似性度量：一種是單個雙向簇的相似性度量，另一種是將這些個體相似度整合到整體得分中的方法。

為了比較單個雙向簇，采用了幾種方法。現在，目前只執行 Jaccard 索引：

其中Ａ和Ｂ是雙向簇, ｜Ａ∩Ｂ｜ 是交叉點的元素數量。

Jaccard 索引達到最小值0，當biclusters完全不同時，Jaccard指數最小值為0;當biclusters完全相同時，Jaccard指數最大值為1。

已經開發了幾種方法來比較兩個雙向簇的集合。目前，只有consensus_score（Hochreiter等人，2010）可用：

  1. 使用Jaccard索引或類似度量， 為每個集合中的雙向簇對計算簇之間的相似性。
  2. 以一對一的方式將雙向簇從一個集合分配給另一個集合，以最大化他們的相似性之和。使用匈牙利算法(Hungarian algorithm)執行此步驟。
  3. 最終的相似度之和除以較大集合的大小。

當所有雙向簇對都完全不相似時，將出現最低共識分數0。當兩個雙向簇集合相同時，出現最高分數為1。

參考文獻: