2.5. 分解成分中的信號（矩陣分解問題）?

2.5.1. 主成分分析（PCA）

2.5.1.1. 準確的PCA和概率解釋（Exact PCA and probabilistic interpretation）

主成分分析（PCA） 是用來對一組連續正交分量的多變量數據集進行方差最大化的分解。 在 scikit-learn 中， PCA 通過 fit 方法可以擬合出 n 個成分來實現一個transformer對象 ， 并且可以將新的數據集投影到這些成分中。

在應用SVD(奇異值分解) 之前, PCA 會把輸入數據的每個特征聚集，而不是縮放輸入數據。可選參數 whiten=True 使得將數據投影到奇異空間成為可能，同時將每個分量縮放到單位方差。 如果下游模型對信號的各向同性做了強假設，這通常是有用的：例如，使用RBF內核的支持向量機算法和 K-Means 聚類算法就是這樣。

以下是iris數據集的一個例子，它由4個特征組成，通過PCA降維后投影到方差最大的二維空間上：

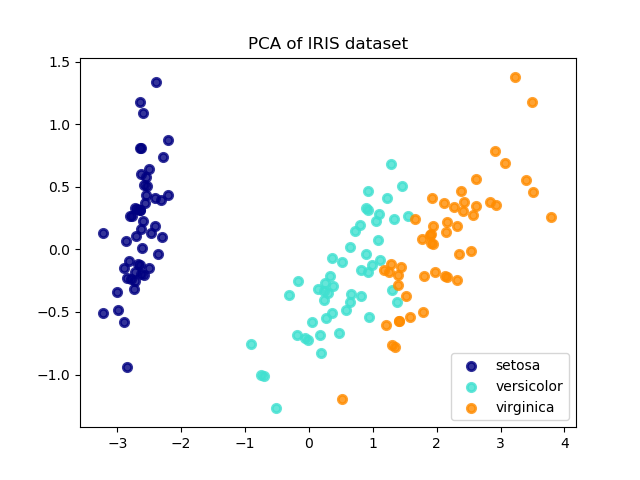
PCA對象還提供了PCA的概率解釋，可以根據解釋的方差給出數據的可能性。因此，PCA實現了一個可以在交叉驗證中使用的評分（score）方法：

示例:

2.5.1.2. 增量PCA (Incremental PCA)

PCA 對象非常有用, 但是對于大型數據集有一定的限制。 最大的限制是 PCA 只支持批處理，這意味著所有要處理的數據必須放在主內存。 IncrementalPCA 對象使用一種不同的處理形式， 即允許部分計算以小型批處理方式處理數據的方法進行, 這些計算結果和 PCA 的結果完全匹配。 IncrementalPCA 可以通過以下方法實現核外主成分分析：

  • 對按順序從本地硬盤或網絡數據庫中獲取的數據塊使用 partial_fit 方法。
  • 在稀疏矩陣或內存映射文件上使用 (通過 numpy.memmap 創建)fit 方法。

IncrementalPCA 類只存儲分量和噪聲方差，以便增量地更新 explainedvariance_ratio _。 這就是為什么內存使用量取決于每批處理的樣本數量，而不是要在數據集中處理的樣本數量。

與PCA一樣，IncrementalPCA在應用SVD之前會把每個特征的輸入數據聚集而不是縮放輸入數據。

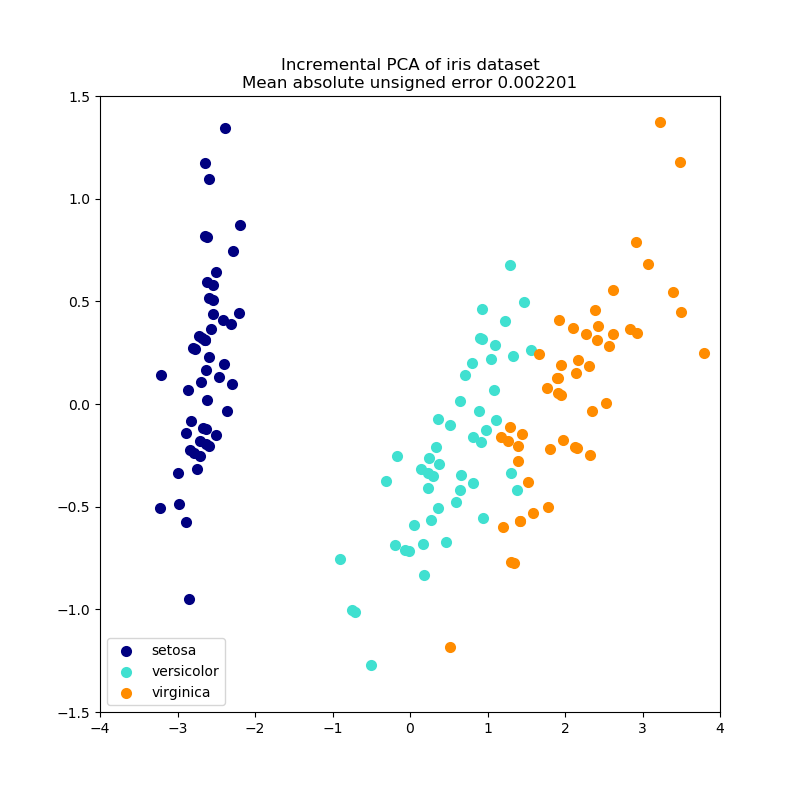
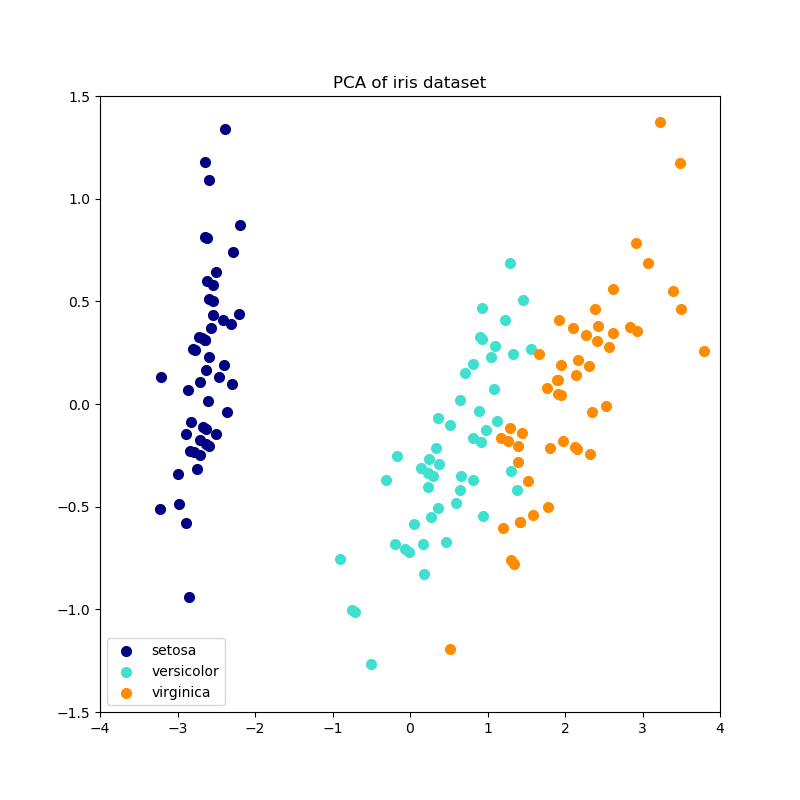
示例：

2.5.1.3. 基于隨機化SVD的PCA

將數據投影到保留大部分方差信息的低維空間通常是有意義的，方法是去掉具有較低奇異值分量的奇異向量。

例如，如果我們使用64x64像素的灰度圖像進行人臉識別，數據的維數為4096，在如此寬的數據上訓練RBF核支持向量機是很慢的。此外，我們知道數據的固有維度比4096要低得多，因為所有的人臉圖片看起來都有些相似。樣本位于一個低得多的維度上(比如200維左右)。主成分分析算法可以對數據進行線性變換，同時降低數據的維數并保留大部分可解釋的方差。

在這種情況下， PCA 使用可選參數 svd_solver='randomized' 是非常有用的：因為我們要放棄大部分的奇異向量，更有效的限制計算奇異向量的近似估計我們將繼續執行轉換。。

例如：下面顯示了來自 Olivetti 數據集的 16 個樣本肖像（以 0.0 為中心）。在右手邊是前16個奇異向量重畫的肖像。由于我們只需要大小為， 的數據集的前16 奇異向量, 計算時間小于 1 秒。

注意：使用可選參數 svd_solver='randomized' ，在 PCA 中我們還需要給出輸入低維空間大小 n_components 。

我們注意到，如果 且，對在PCA中實現的精確方法，隨機 PCA 的時間復雜度是 而不是 。

隨機 PCA 的內存占用量和 成正比，而不是和精確方法的 成正比。

注意：選擇參數 svd_solver='randomized' 的 PCA 的 inverse_transform 的實現, 并不是對應 transform 的精確逆變換，即使參數設置為 whiten=False（默認設置）

示例：

參考文獻：

2.5.1.4. 核主成分分析（Kernel PCA）

KernelPCA 是 PCA 的擴展，通過使用核方法實現非線性降維 (見 Pairwise metrics, Affinities and Kernels) 。 它具有許多應用，包括去噪, 壓縮和結構化預測內核依賴估計(kernel dependency estimation)。 KernelPCA 同時支持 transform 和 inverse_transform 。

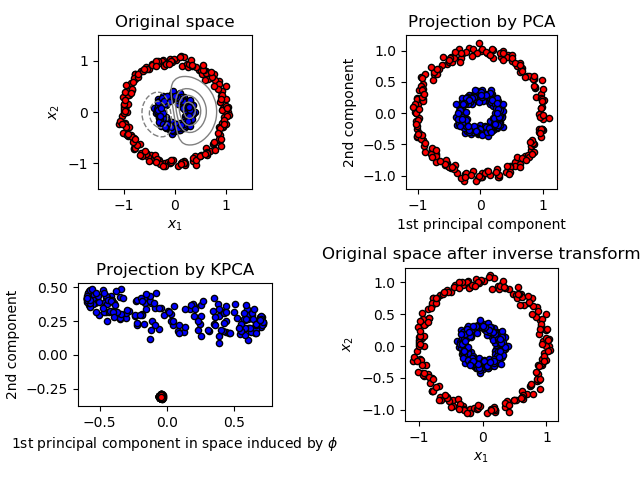
示例：

2.5.1.5. 稀疏主成分分析 ( SparsePCA 和 MiniBatchSparsePCA )

SparsePCA 是 PCA 的一個變體，其目標是提取一組稀疏分量集合，以最大程度地重構數據。

小批量稀疏 PCA ( MiniBatchSparsePCA ) 是 SparsePCA 的一個變體，速度更快，但精度更低。在給定迭代次數的情況下，通過迭代該組特征的小塊來提高速度。

主成分分析(PCA)的缺點是，該方法提取的分量具有完全密集的表達式，即當用原變量的線性組合表示時，系數不為零。這可能使解釋變得困難。在許多情況下，可以把真正的基礎分量被更自然地想象為稀疏向量; 例如在人臉識別中，每個分量可能自然地映射到人臉的各個部分。

稀疏主成分產生了一種更簡潔的、可解釋的表示，明確地強調了哪些原始特征導致了樣本之間的差異。

下面的例子演示了使用稀疏PCA從Olivetti 人臉數據集中提取的16個分量。可以看出正則化項產生了許多0。可以看出正則化項是如何產生了許多0。此外，數據的自然結構使非零系數垂直相鄰。從數學上講，該模型沒有強制執行:每個分量都是一個向量，每個分量都是一個向量 ，除非人性化地將其可視化為 64x64 像素的圖像，否則沒有垂直相鄰性的概念。下面顯示的分量出現局部是數據固有結構的影響，使得這種局部模式使重建誤差最小化。存在考慮到鄰接性和不同結構類型的稀疏導致的規范，參見 [Jen09] 查看這些方法。有關如何使用稀疏PCA的更多細節，請參見下面的示例部分。

注意，對于計算稀疏PCA問題有許多不同的公式。 這里使用的方法基于 [Mrl09] 。所解決的優化問題是一個帶是一個帶有懲罰項 （L1范數的）的 PCA 問題（字典學習）:

在訓練樣本很少時，sparsity-inducing ?1也可以避免擬合噪聲。懲罰的程度(稀疏性)可以通過設置超參數 alpha 來調整）。值較小的值導致溫和的正則化因子分解，而較大的值將許多系數收縮到零。

注意 ：

雖然按照在線算法的精神，但因為在線算法是以特征為導向，而不是以樣本為導向。 MiniBatchSparsePCA 類不能實現 partial_fit。

注意：

示例：

參考資料：

2.5.2. 截斷奇異值分解和隱語義分析

TruncatedSVD 實現了一種奇異值分解（SVD）的變體，它只計算 個最大的奇異值，其中 是用戶指定的參數。

當截斷的 SVD被應用于 term-document矩陣（由 CountVectorizer 或 TfidfVectorizer 返回）時，這種轉換被稱為 潛在語義分析latent semantic analysis (LSA)，因為它將這些矩陣轉換為低維的"語義"空間。眾所周知，特別是 LSA 會對抗同義詞和一詞多義（它們都大致表示每個單詞有多個含義）的影響, 這種影響會導致 term-document 矩陣過于稀疏，并且在余弦相似度等度量條件下表現出較差的相似性。

注意 : LSA也被稱為潛在語義索引(LSI)，盡管嚴格來說它指的是用于信息檢索目的的持久索引。

從數學角度來說，截斷的SVD應用于訓練樣本用截斷的SVD 會產生一個低秩近似值:

在這個操作之后， 是包括 個特征的轉換后的訓練集（在 API 中被稱為 n_components ） 。

還需要轉換一個測試集 , 我們乘以 :

注意，在自然語言處理(NLP) 和信息檢索(IR) 文獻中， LSA 的大多數處理都是交換矩陣 的坐標軸,使其具有 n_features × n_samples 的形狀。 我們 在 scikit-learn API 用一種不同的方式表示 LSA, 但是找到的奇異值是相同的。

TruncatedSVD 與 PCA非常類似，但不同之處在于矩陣 不需要居中。當從特征值按列（每個特征）減去 的均值時，在得到的矩陣上應用截斷的SVD 相當于 PCA 。 實際上，，因為即使對于中等規模的文檔集合， 密集化也可能填滿內存。

盡管 TruncatedSVD 轉換器可以在任何特征矩陣上工作，但還是建議在 LSA/文檔處理設置中，在 tf–idf 矩陣上的原始頻率計數使用它。特別地，(sublinear_tf=True, use_idf=True) ，以使特征值更接近于高斯分布，從而補償 LSA 對文本數據的錯誤假設。

示例:

參考資料:

2.5.3. 詞典學習

2.5.3.1. 帶有預計算詞典的稀疏編碼

SparseCoder 對象是一種估計器 ，因此，此對象不實現fit方法。這種轉換相當于一個稀疏編碼問題。 將數據的表示為盡可能少的詞典原子的線性組合。 詞典學習的所有變體以盡可能少的字典原子的線性組合來尋找數據的表示。字典學習的所有變體實現以下變換方法，通過 transform_method 初始化參數進行控制:

  • Orthogonal matching pursuit (正交匹配追蹤法（OMP）)
  • Least-angle regression (最小角度回歸)
  • Lasso computed by least-angle regression(最小角度回歸的Lasso 計算)
  • Lasso using coordinate descent ( 使用坐標下降的Lasso)(Lasso)
  • Thresholding(閾值)

閾值方法速度非常快，但是不能產生精確的重建。它們在文獻分類任務中被證明是有用的。對于圖像重建任務，正交匹配追蹤可以得到最精確、無偏的重建結果。

字典學習對象通過 split_code 參數提供稀疏編碼結果中分離正值和負值的可能性。當使用詞典學習提取將用于監督學習的特征時，這是很有用的，因為它允許學習算法將不同的權重從正加載（loading）分配給相應的負加載。

單個樣本的分割編碼長度為 2 * n_components ，并使用以下規則構造: 首先，計算長度為 n_components 的常規編碼。然后， split_code 的第一個 n_components 條目填充常規編碼向量的正部分。分割編碼的另一半用編碼向量的負部分填充，只有一個正號。因此， split_code 是非負的。

示例:

2.5.3.2. Generic dictionary learning（通用字典學習）

詞典學習( DictionaryLearning ) 是一個矩陣因式分解問題，相當于找到一個(通常過于完整的)字典對擬合數據進行稀疏編碼。

將數據表示為過完備字典的原子的稀疏組合被認為是哺乳動物初級視覺皮層的工作方式。因此，字典學習應用于圖像修補，已被證明在圖像處理任務，如圖像完成，修復和去噪，以及有監督識別任務中表現良好。

字典學習是一個優化問題，通過交替更新稀疏代碼來解決，作為解決多個Lasso問題的解決方案，考慮字典固定，然后更新字典以最大程度擬合稀疏代碼。

在使用這樣的過程來適應字典之后，變換只是一個稀疏編碼步驟，與所有字典學習對象共享相同的實現。(見 帶有預計算詞典的稀疏編碼)。

也可以將字典和/或編碼約束為正以匹配數據中可能表現的約束。以下是應用不同正約束的人臉。紅色表示負值, 藍色表示正值,白色表示零。

下圖展示了字典是如何從部分浣熊臉部圖像中提取4x4像素圖像補丁中進行詞典學習。

示例:

參考資料:

2.5.3.3. 小批量字典學習

MiniBatchDictionaryLearning 實現了一種更快但精確度下降的詞典學習算法，更適合于大型數據集。

默認情況下，MiniBatchDictionaryLearning 將數據分成小批量，并以在線方式進行優化，方法是通過在指定次數的迭代中循環使用小批量。但是，它目前沒有實現停止條件。

估計器還實現了 partial_fit, 它通過在一個小批處理中僅迭代一次來更新字典。 當在線學習的數據從一開始就不容易獲得，或者數據超出內存時，可以使用這種迭代方法。

詞典學習聚類

請注意，當使用字典學習來提取表示(例如稀疏編碼)時，聚類是學習字典的一個很好的中間方法。 例如，MiniBatchKMeans 估計器能高效計算并使用 partial_fit 方法實現在線學習。

示例: 在線學習人臉部分的字典 Online learning of a dictionary of parts of faces

2.5.4. 因子分析

在無監督學習中，我們只有一個數據集 。如何用數學描述這個數據集？ 的一個非常簡單的連續隱變量模型。

向量 被稱為’隱性的（latent )'因為它是不可觀測的。 為均值為 0 ，協方差為 的符合高斯分布的噪聲項，

是偏置向量，這種模型被稱為“生成的”，因為它描述了 如何生成 。如果我們使用所有的 作為列來形成一個矩陣 ，并將所有的 作為矩陣 的列，然后我們可以寫(用適當的定義 和 ):

換句話說，我們分解矩陣 ,如果給出 ,上述方程自動地表示以下概率解釋：

對于一個完整的概率模型，我們還需要隱變量 的先驗分布。 最直接的假設（基于高斯分布的優良性質）是 。這產生一個高斯分布作為 邊際分布:

現在，在沒有任何進一步假設的前提下，有一個隱變量 是多余的， 完全可以用均值和協方差來建模。 我們需要對這兩個參數之一施加一些更具體的構造。 誤差協方差的一個簡單的附加假設是 構造: 這個假設導致的概率模型PCA。 此模型稱為 FactorAnalysis，是經典的統計模型。矩陣W有時被稱為“因子加載矩陣”。

兩個模型原則上都可以使用低階協方差矩陣來估計高斯分布。由于兩個模型都是概率模型，因此可以將它們集成到更復雜的模型中，例如，因子分析器的混合。如果隱變量基于非高斯分布的先驗，則得到的模型會完全不同（例如， FastICA ）。

因子分析可以產生與PCA類似的分量（例如其加載矩陣的列）。 然而，不能對這些分量做任何一般性聲明（例如，它們是否正交）:

PCA與之相比，因子分析的主要優勢在于它可以獨立地模擬輸入空間各個方向上的方差（異方差噪聲）：

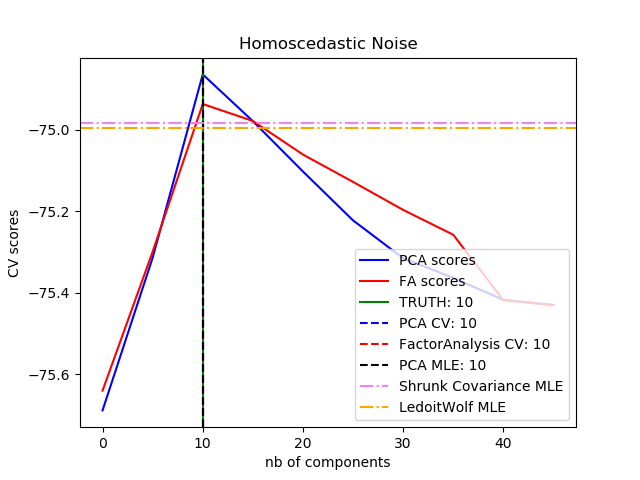
與存在異方差噪聲的概率PCA相比，這可以提供更好的模型選擇：

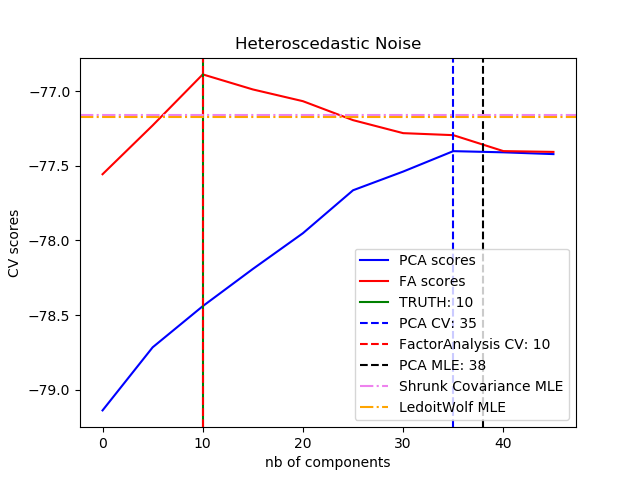
示例:

2.5.5. 獨立成分分析（ICA）

獨立成分分析將一個多元信號分解成獨立性最強的可加子成分。 它利用 Fast ICA 算法在 scikit-learn 中實現。通常，ICA不用于降低維度，而是用于分離疊加信號。由于ICA模型不包含噪聲項，為了使模型正確，必須進行白化處理。這可以在內部使用whiten參數完成，也可以手動使用某種PCA變體。

ICA 通常用于分離混合信號（一個稱為盲源分離的問題），如下例所示:

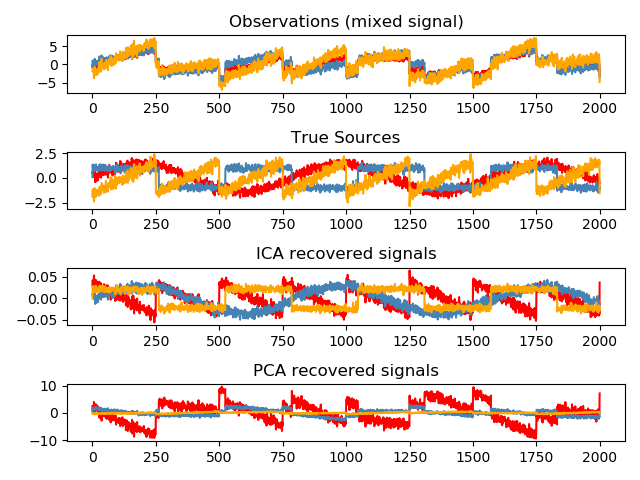ICA 也可以用于尋找具有稀疏性的分量的非線性分解:

示例：

2.5.6. 非負矩陣分解(NMF 或 NNMF)

2.5.6.1. NMF 與 Frobenius 范數

NMF [1]是另一種降維方法,它假設數據和分量是非負的。 在數據矩陣不包含負值的情況下，可以插入 NMF 而不是 PCA 或其變體。 通過優化樣本 與矩陣乘積 之間的距離 ，可以將樣本 分解為兩個非負矩陣 和 。使用最廣泛的距離函數是 Frobenius 平方范數，它是歐氏范數在矩陣上的推廣:

與 PCA 不同的是，向量的表示是通過相加的方式得到的，通過疊加分量而不是減去分量。這種加性模型對于表示圖像和文本非常有效。

[Hoyer, 2004] [2] 研究表明，當處于一定約束時，NMF 可以產生基于某一部分數據集的表示，從而產生可解釋的模型。以下示例展示了與 PCA 特征人臉相比， NMF 從 Olivetti 面部數據集中的圖像中找到的的16個稀疏分量。

init 屬性決定應用的初始化方法，這對方法的性能有很大的影響。NMF 實現了非負的雙奇異值分解方法。NNDSVD [4]基于兩個 SVD 過程，一個對數據矩陣進行近似,另一個是對得到的SVD因子的正部分利用單位秩矩陣的代數特性進行近似。基本的 NNDSVD 算法更適合稀疏分解。其變體 NNDSVDa（在這種情況下，所有的0都被設置為數據所有元素的平均值）和 NNDSVDar（在這種情況下，所有的0都被設置為小于數據除以100的平均值的隨機擾動）推薦用于稠密情況。

注意，乘法更新(' mu ')求解器不能更新初始化中出現的零，因此與引入大量零的基本NNDSVD算法聯合使用會導致較差的結果;在這種情況下，建議使用NNDSVDa或NNDSVDar。

通過設置 init="random"，使用正確縮放的隨機非負矩陣也可以初始化 NMF。 也可以將整數種子或 RandomState 傳遞給 random_state 以控制重現性。

在 NMF 中，可以在損失函數中加入L1和L2先驗使模型正則化。 L2 先驗使用 Frobenius 范數，而L1 先驗使用 L1 范數。在 ElasticNet 中， 我們通過 l1_ratio ( ) 參數和正則化強度參數 alpha ()來控制 L1 和 L2 的組合。那么先驗條件是:

正則化目標函數為:

NMF 正則化 W 和 H 。公共函數 non_negative_factorization 允許通過 regularization 屬性進行更精細的控制，將W ，H分別 或兩者都進行正則化。

2.5.6.2. 具有 beta-divergence 的 NMF

如前所述，使用最廣泛的距離函數是Frobenius 平方范數，它是歐氏范數在矩陣上的一個明顯的擴展應用:

其他距離函數可用于 NMF，例如（廣義） Kullback-Leibler(KL) 散度，也稱為 I-divergence:

或者， Itakura-Saito(IS) divergence:

這三個距離函數是 beta-divergence 函數的特殊情況，其參數分別為 [6] 。 beta-divergence 定義如下:

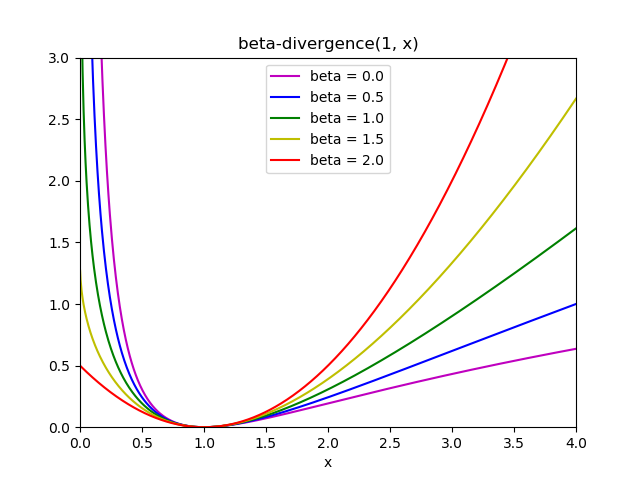注意在 上定義無效，但它可以連續擴展到 和

NMF 實現了兩個求解器，分別使用了坐標下降 ( ‘cd’) [5]和乘法更新( ‘mu’) [6]。 ‘mu’ 求解器可以優化每個 beta 散度，包括 Frobenius 范數 () ，（廣義的） Kullback-Leibler 散度 （）和Itakura-Saito 散度（））。注意對于 ，’mu’ 求解器明顯快于 取其他值。還要注意， 如果是負數（或0，即 ‘itakura-saito’ ） ，輸入矩陣不能包含零值。

‘cd’ 求解器只能優化 Frobenius 范數。由于 NMF 的非凸性，即使優化相同的距離函數時，不同的解也可能會收斂到不同的最小值。

NMF最適用于 fit_transform 方法，該方法返回矩陣W。矩陣 H 被存儲到擬合模型中的components_ 屬性; 方法 transform 將基于這些存儲的分量分解一個新的矩陣 X_new:

>>> import numpy as np
>>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]])
>>> from sklearn.decomposition import NMF
>>> model = NMF(n_components=2, init='random', random_state=0)
>>> W = model.fit_transform(X)
>>> H = model.components_
>>> X_new = np.array([[1, 0], [1, 6.1], [1, 0], [1, 4], [3.2, 1], [0, 4]])
>>> W_new = model.transform(X_new)

示例:

參考資料;

2.5.7. 隱 Dirichlet 分配（LDA）

隱 Dirichlet 分配是離散數據集的集合（如文本語料庫）的生成概率模型。 它也是一個主題模型，用于從文檔集合中發現抽象主題。

LDA 的圖形模型是一個三級生成模型:

注意上面的圖形模型中的符號，可以在Hoffman et al.(2013)中找到:

  • 語料庫是文檔的集合。

  • 文檔是單詞的序列。

  • 語料庫中有主題。

  • 這些方框代表重復采樣。

在圖形模型中，每個節點都是隨機變量，在生成過程中都有作用。有陰影的節點表示觀察到的變量，無陰影的節點表示隱藏(潛在的)變量。在這種情況下，語料庫中的單詞是我們觀察到的唯一數據。潛在變量決定了語料庫中主題的隨機混合和文檔中詞匯的分布。LDA的目標是利用觀察到的詞來推斷隱藏的主題結構。

在對文本語料庫進行建模時，該模型假設以下語料庫的生成過程 文件和 主題， 對應與API中的n_components：

  1. 對于每個主題 ， 繪制 Dirichlet 。這提供了單詞的分布，即單詞出現在主題中的概率。 對應于topic_word_prior。

  2. 對于每個文檔 ，繪制主題比例 Dirichlet 。 對應于doc_topic_prior。

  3. 對在文件中 中的每個單詞：

  4. 繪制主題分配： Multinomial

  5. 觀察到的單詞： Multinomial

對于參數估計，后驗分布為:

由于后驗是很難處理，因此變分貝葉斯方法使用一個更簡單的分布 來近似它，對這些變分參數進行優化，使(ELBO)最大化:

最大化ELBO等效于最小化 和 后驗 之間的 Kullback-Leibler(KL) 散度。

LatentDirichletAllocation實現在線變分貝葉斯算法，并支持在線和批量更新方法。批處理方法在每次完整遍歷數據后更新變量，而在線方法則從小批量數據點更新變量。

注:雖然在線方法保證收斂到局部最優點，但最優點的質量和收斂速度可能取決于小批量的大小和與學習速率設置相關的屬性。

當LatentDirichletAllocation應用于“文檔項”矩陣時，該矩陣將被分解為一個“主題項”矩陣和一個“文檔項”矩陣。在模型中，“主題-術語”矩陣components_與模型一樣存儲，但“文檔-主題”矩陣可以通過transform方法進行計算。

LatentDirichletAllocation還實現partial_fit方法。當可以按順序獲取數據時，就使用這種方法。

示例：

參考文獻：

參見 Neighborhood Components Analysis 的降維方式.