2.1. 高斯混合模型?

sklearn.mixture是一種采用高斯混合模型進行非監督學習的包，（支持 diagonal，spherical，tied，full 四種類型的協方差矩陣）可以對數據進行采樣并估計，同時該包也提供了幫助用戶決定合適分量個數的功能。

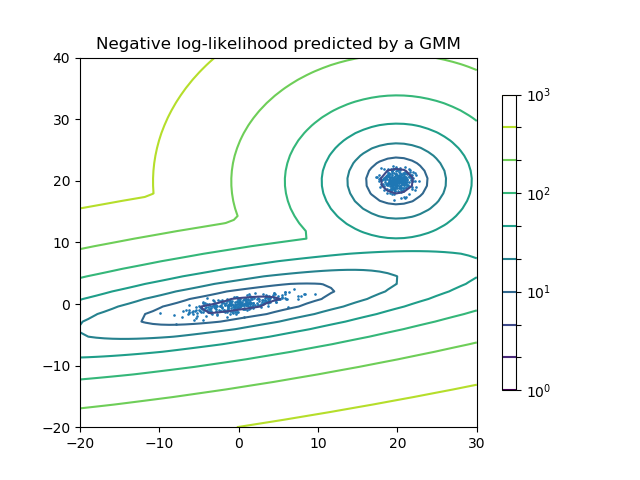二分量高斯混合模型: 數據點，以及模型的等概率線。

高斯混合模型是一種概率模型，它假設所有數據點都是從有限數量的高斯分布的混合參數中生成的。可以將混合模型視為對 k-means聚類算法的擴展，它包含了數據的協方差結構以及隱高斯模型中心的信息。

對于不同的估算策略，Scikit-learn采用不同的類來預測高斯混合模型。下面將詳細介紹：

2.1.1. 高斯混合

該GaussianMixture對象實現了用于擬合高斯混合模型的 期望最大化（EM）算法。它還可以為多元模型繪制置信橢圓體，并計算貝葉斯信息準則以評估數據中的聚類數量。GaussianMixture.fit可以從訓練數據中擬合出一個高斯混合模型。在給定測試數據的情況下，使用該GaussianMixture.predict方法可以為每個樣本分配最適合它的高斯分布模型。。

GaussianMixture帶有不同的選項來約束不同的的協方差估計：spherical，diagonal，tied 或 full 協方差。

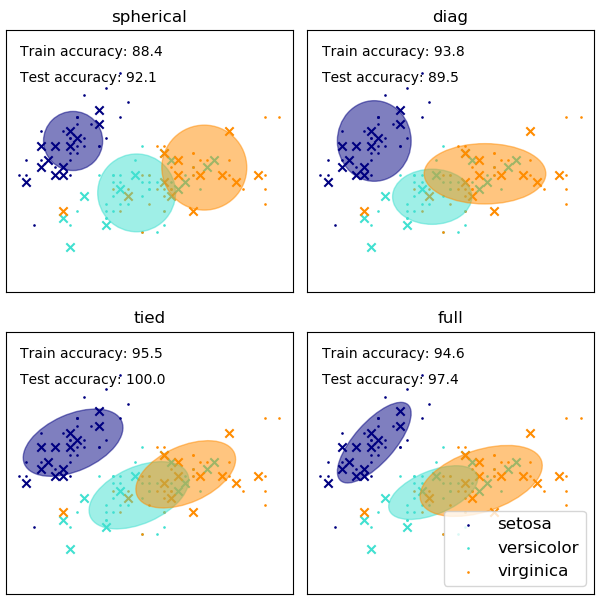
示例:

2.1.1.1. 優缺點GaussianMixture

2.1.1.1.1 優點

  • 速度：它是混合模型學習算法中的最快算法
  • 無偏差性：由于此算法僅最大化可能性，因此不會使均值趨于零，也不會使聚類大小具有可能適用或不適用的特定結構。

2.1.1.1.2 缺點

  • 奇異性：當每個混合模型的點數不足時，估計協方差矩陣將變得困難，并且除非對協方差進行人為正則化，否則該算法會發散并尋找無窮大似然函數值的解。
  • 分量數量：該算法將始終使用它可以使用的所有分量，所以在沒有外部提示的情況下，需要留存數據或者信息理論標準來決定用多少個分量。

2.1.1.2. 選擇經典高斯混合模型中分量的個數

采用BIC可以有效的選擇高斯混合中的分量個數。理論上講，它僅在近似狀態下（即，如果有大量數據可用并假設數據實際上是由一個混合高斯模型生成）才能恢復模型的真實分量數。請注意，使用變分貝葉斯高斯混合 可避免指定高斯混合模型的分量數。

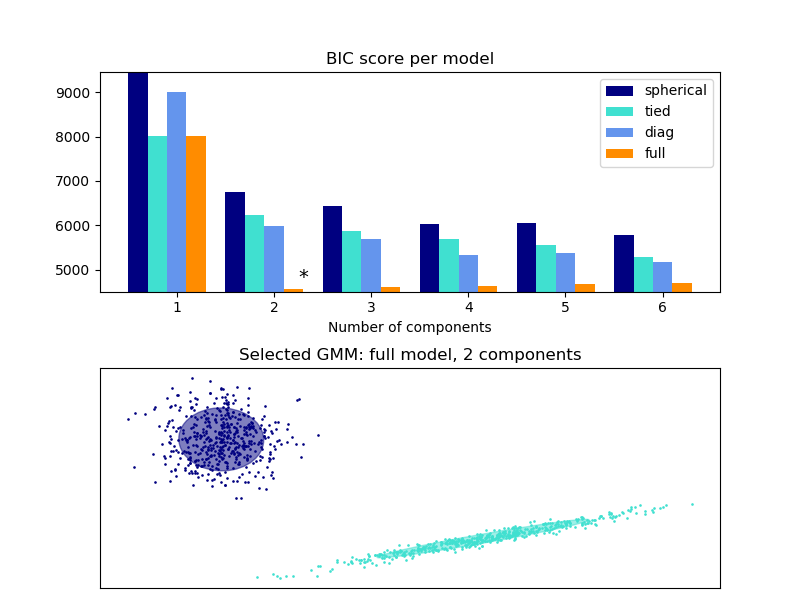示例:

2.1.1.3. 估計算法期望最大化

從未標記的數據中學習高斯混合模型的主要困難在于，通常不知道哪個點來自哪個隱分量（如果可以得到這些信息，則很容易通過相應的數據點，擬合每個獨立的高斯分布）。Expectation-maximization 是一種基于迭代來解決此問題的可靠統計算法。首先假設一個隨機分量（隨機地選取一個數據點為中心點，該點可以由k-means算法獲得，也可以原點附近的正態分布點），并為每個點計算由模型的每個分量生成的概率。然后，調整模型參數以最大化模型生成這些參數的可能性。重復此過程可確保始終收斂到一個局部最優值。

2.1.2. 變分貝葉斯高斯混合

BayesianGaussianMixture對象是高斯混合模型的變體，使用變分推理算法實現。該API和 GaussianMixture 所定義的API類似。

2.1.2.1. 估計算法：變分推斷

變分推理是期望最大化算法的擴展，它最大化了模型證據（包括先驗）的下界，而不是數據的似然概率。變分方法背后的原理與期望最大化相同（兩者都是迭代算法，在找到每種模型混合生成的每個點的概率與將模型擬合到這些分配的點之間交替進行），但變分方法通過整合來自先驗分布的信息添加正則化。這避免了通常在期望最大化算法中發現的奇異性，但也為模型引入了一些細微的偏差。推理過程通常明顯變慢，但一般也不會慢到無法使用。

由于其貝葉斯性質，變分算法需要比期望最大化更多的超參數，其中最重要的是濃度參數weight_concentration_prior。為先驗濃度指定一個較低的值將使模型將大部分權重分配給少數分量，這樣其余組分的權重就接近于零。先驗的高濃度值將允許混合中有更多的分量在混合模型中都有相當比例的權重。

BayesianGaussianMixture類的參數實現權重分布提出了兩種先驗類型：具有Dirichlet distribution(狄利克雷分布)的有限混合模型和具有 Dirichlet Process（狄利克雷過程）的無限混合模型。在實踐中，Dirichlet Process推理算法是近似的，并使用具有固定最大分量數的截斷分布（稱為“Stick-breaking representation”）。實際使用的分量數量幾乎總是依賴數據。

下圖比較了不同類型的加權濃度先驗（參數weight_concentration_prior_type）對比不同類型的加權濃度先驗所獲得的結果weight_concentration_prior。在這里，我們可以看到weight_concentration_prior參數的值對獲得的有效激活的分量數有很大的影響。還可以注意到，當先驗類型為'dirichlet_distribution'時，先驗濃度權重較大會導致權重更均勻，而'dirichlet_process'類型（默認類型）不一定如此。

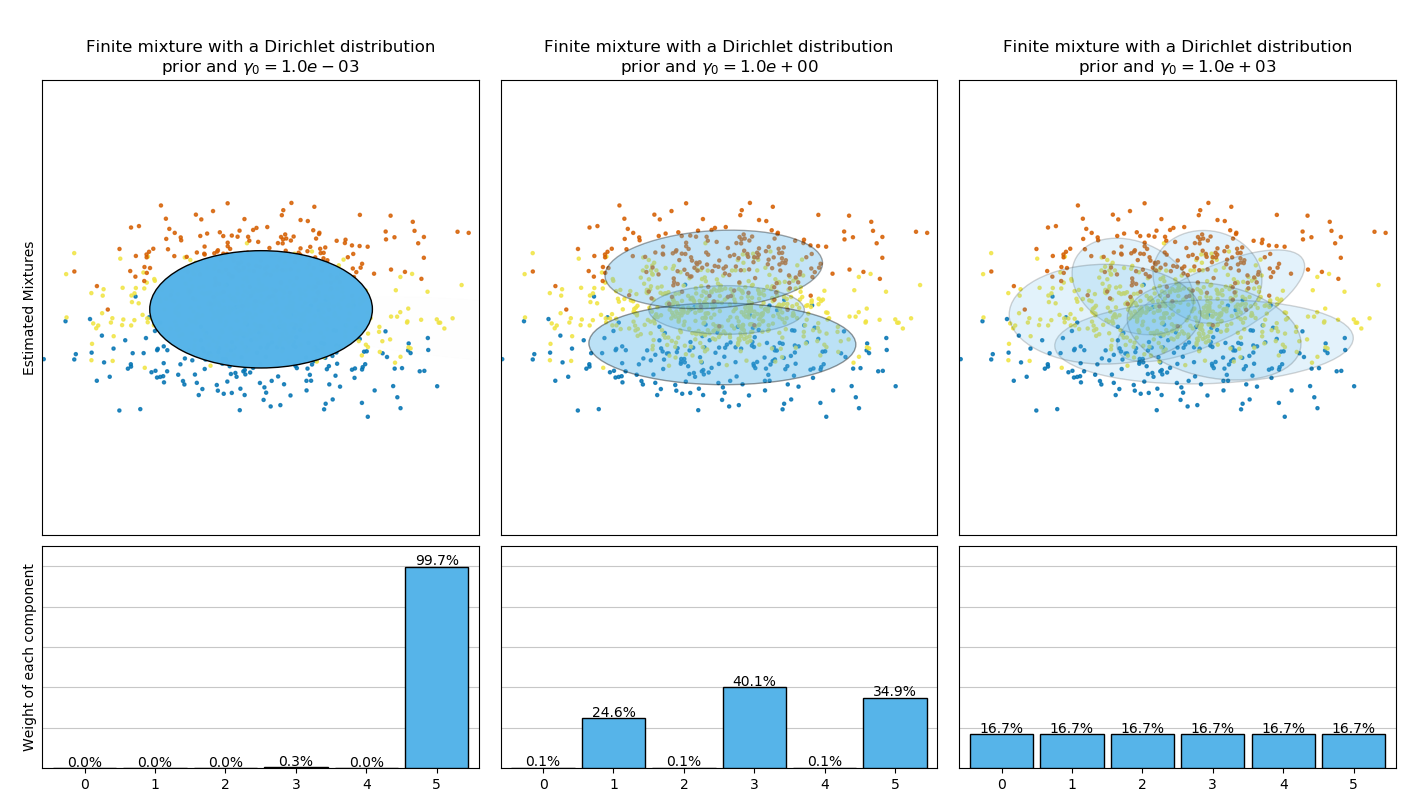
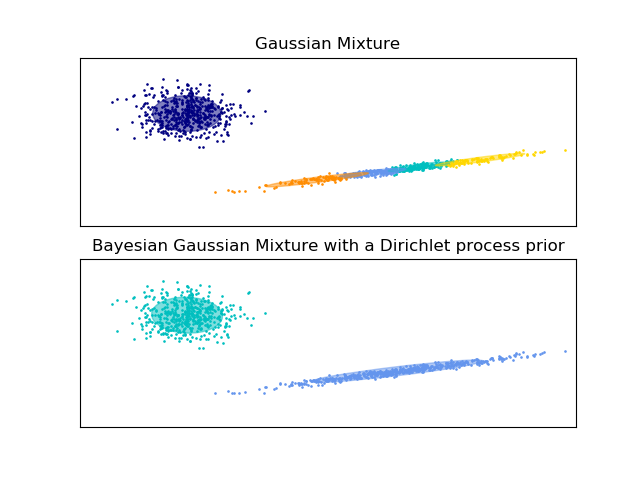
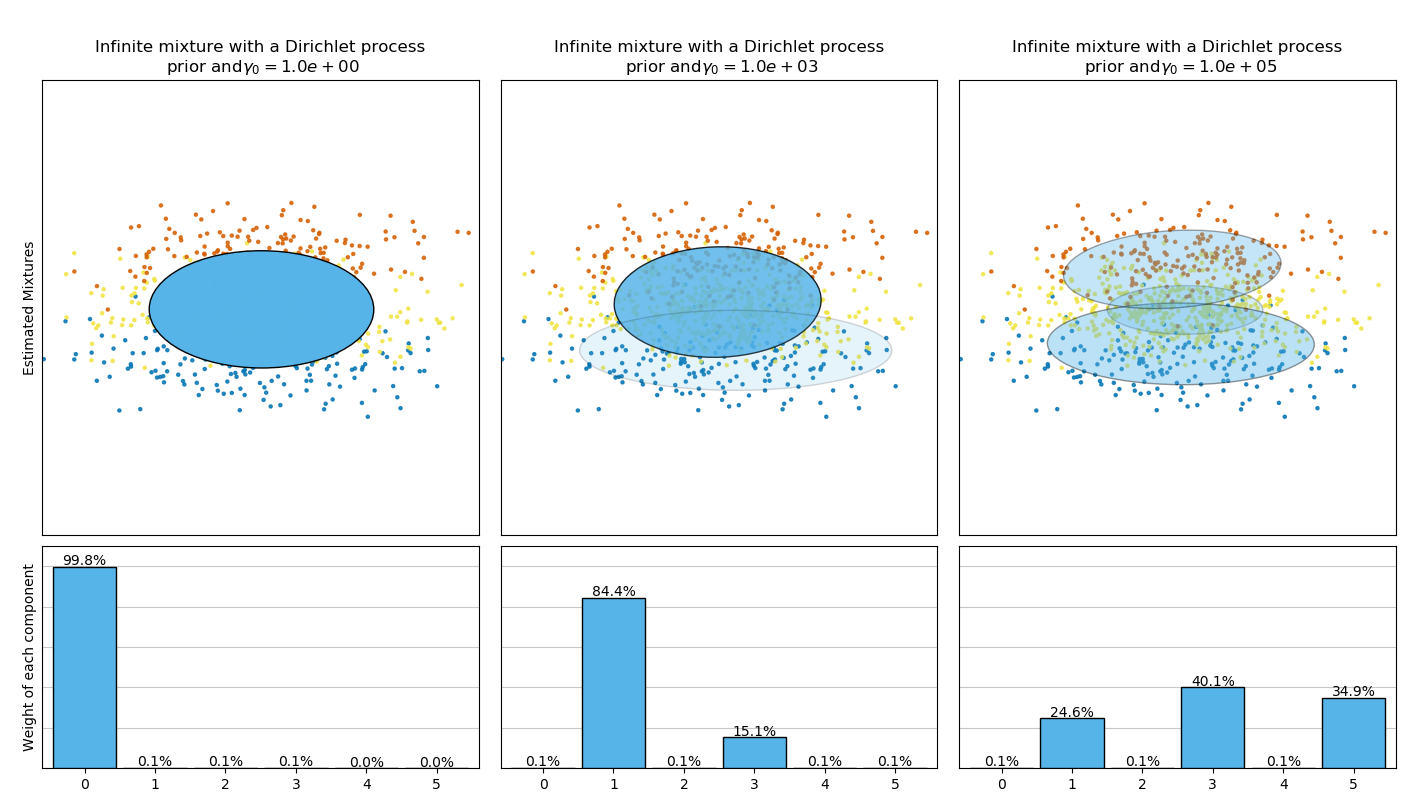下面的示例將具有固定數量分量的高斯混合模型與先驗Dirichlet process prior（狄利克雷過程先驗）的變分高斯混合模型進行了比較。在這里，一個經典的高斯混合模型在由2個聚類組成的數據集，具有5個分量。我們可以看到具有Dirichlet過程先驗的變分高斯混合模型能夠將自身限制為僅2個分量，而高斯混合將數據與具有固定數量的分量擬合時用戶必須事先設置固定數量的分量。在該示例中，用戶選擇 n_components=5，與真正的試用數據集（toy dataset）的生成分量數量不符。很容易注意到, 狄利克雷過程先驗的變分高斯混合模型可以采取保守的策略，僅擬合生成一個分量。

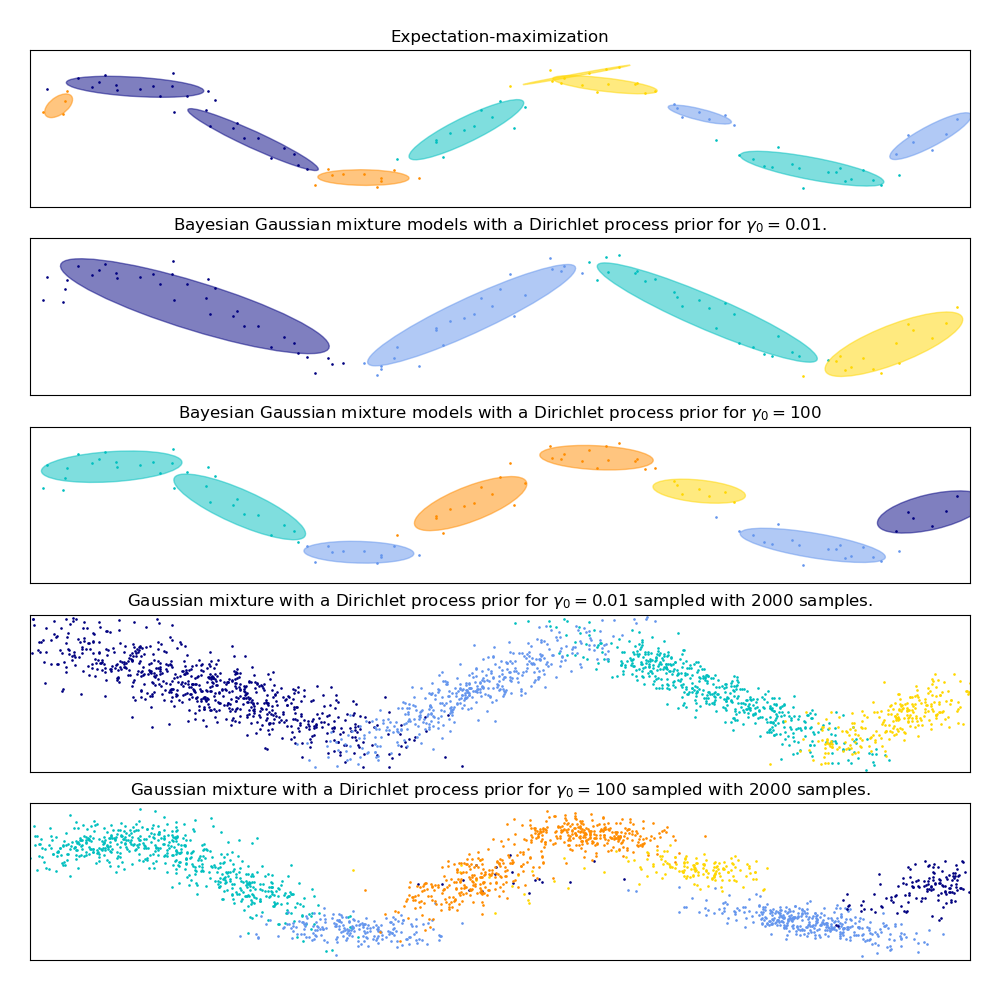
在下圖中，我們將擬合一個并不能被高斯混合模型很好描述的數據集。 調整 BayesianGaussianMixture 類的參數 weight_concentration_prior ，這個參數決定了用來擬合數據的分量數量。我們在最后兩個圖上展示了從兩個混合結果中產生的隨機抽樣。

示例:

2.1.2.2. BayesianGaussianMixture 下的變分推理的優缺點

2.1.2.2.1. 優點

  • 自動選擇: 當 weight_concentration_prior 足夠小且 n_components 大于模型所需要的值時，變分貝葉斯混合模型自然會傾向于將某些混合權重值設置為接近零。 這樣就可以讓模型自動選擇合適數量的有效分量。過程僅需要提供分量的數量上限。但是注意，“理想” 的激活分量數量是針對特定應用的，在設置數據挖掘參數時通常并不明確。
  • 對參數數量的敏感度較低: 與有限模型不同，有限模型幾乎總是盡可能多地使用分量，因此對于不同數量的分量將產生完全不同的解決方案, 而Dirichlet過程的先驗的變分推理（weight_concentration_prior_type='dirichlet_process'）的輸出并不總隨參數的變化而變化, 因此該變分推理更加穩定且需要更少的調優。
  • 正則化: 由于結合了先驗信息，因此變分的解比期望最大化（EM）的解有更少的病理特征。

2.1.2.2.2. 缺點

  • 速度: 變分推理所需要的額外參數化使推理變慢，盡管幅度不大。
  • 超參數: 該算法需要一個額外的超參數，可能需要通過交叉驗證進行實驗調優的超參數。
  • 偏差: 在推理算法中（以及在使用Dirichlet過程中）存在許多隱含的偏差， 并且只要這些偏差與數據之間不匹配，就有可能使用有限模型來擬合出更好的模型。

2.1.2.3. The Dirichlet Process（狄利克雷過程）

本文描述了狄利克雷過程混合的變分推理算法。狄利克雷過程是在分區數無限、無限大的聚類上的先驗概率分布。與有限高斯混合模型相比，變分技術使我們在推理時間上幾乎不受懲罰的納入了高斯混合模型的先驗結構。

一個重要的問題是，Dirichlet過程如何使用無窮多的聚類數，并且結果仍然保持一致。雖然本手冊沒有做出完整的解釋，但你可以參考 stick breaking process來幫助理解它。是狄利克雷過程的衍生。我們從一個單位長度的 stick 開始，在每一步都折斷剩下的 stick 的一部分。每一次，我們把 stick 的長度聯想成所有點里落入一組混合的點的比例。 最后，為了表示無限混合，我們把 stick 的最后剩余部分聯想成沒有落入其他組的點的比例。每段的長度是一個隨機變量, 其概率與濃度參數成正比。較小的濃度值將把單位長度分成更大的 stick 段（定義更集中的分布）。濃度值越大， stick 段越小（即增加非零權重的分量數量）。

在對該無限混合模型進行有限近似的情形下狄利克雷過程的變分推理技術仍然可以使用。我們不必事先指定想要的分量數量，只需要指定濃度參數和混合分量數的上界（假定上界高于“真實”的分量數，這僅僅影響算法復雜度，而不是實際使用的分量數量）。