3.5 驗證曲線：繪制分數以評估模型?

每一個估計器都有其優勢和劣勢。它的泛化誤差可以分解為偏差，方差和噪聲。估計器的偏差是不同訓練集的平均誤差。估計器的方差表示對不同訓練集，模型的敏感度。噪聲是數據的特質。

在下圖中，可以看見一個函數和函數中的一些噪聲數據。使用三種不同的估計器來擬合函數：帶有自由度為1，4和15的二項式特征的線性回歸。第一個估計器最多只能提供一個樣本與真實函數間不好的擬合，因為該函數太過簡單，第二個估計器估計的很好，最后一個估計器估計訓練數據很好，但是不能擬合真實的函數，例如對各種訓練數據敏感（高方差）。

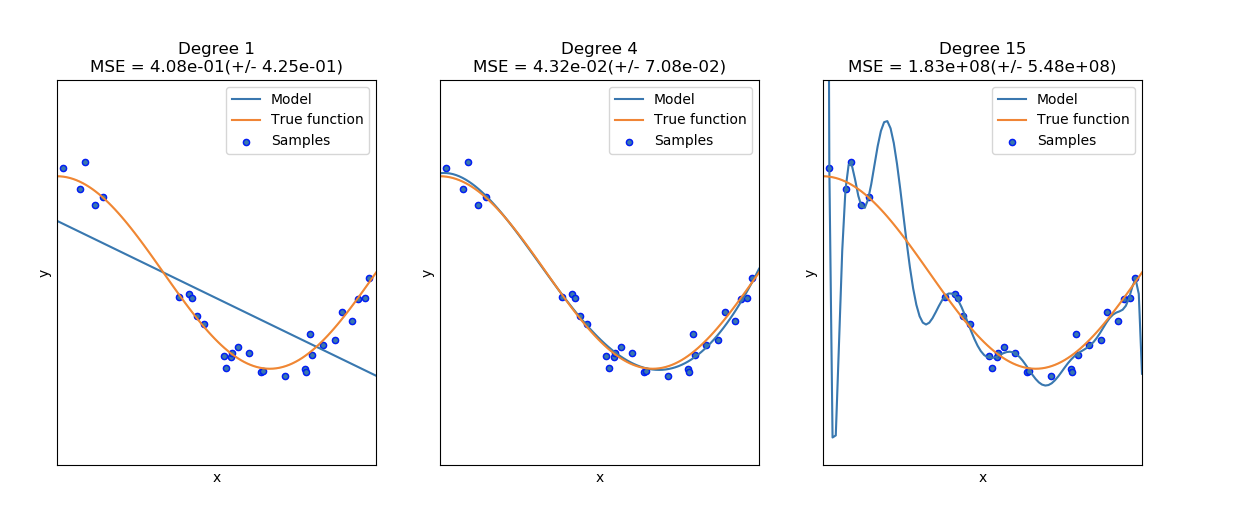偏差和方差是估計器固有的特質，我們經常選擇學習算法和超參數，以使偏差和方差都盡可能小（參見Bias-variance dilemma）。另一個減少模型方差的方法是使用更多的訓練數據。但是，如果真實函數太過復雜才能估計出一個低方差的估計器，你只能收集更多訓練集數據。

在一個簡單的一維問題中，可以很容易看見估計器是否收到偏差或者方差的影響。但是，在高維空間中，模型很難被可視化。因為這個原因，使用工具來描述就很有用。

例子：

• 欠擬合和過擬合
• 繪制驗證曲線
• 繪制學習曲線

3.5.1 驗證曲線

需要一個評分函數（詳見 度量和評分：量化預測的質量）以驗證一個模型，例如分類器的準確率。選擇一個估計器的多個超參數的好方法當然是網格搜索或者相類似的方法（詳見 調整估計器的超參數）通過選擇超參數以使在驗證集或者多個驗證集的分數最大化。需要注意的是：如果基于驗證分數優化超參數，驗證分數是有偏的并且不是好的泛化估計。為了得到一個好的泛化估計，可以通過計算在另一個測試集上的分數。

但是，有時繪制在訓練集上單個參數的影響曲線也是有意義的，并且驗證分數可以找到對于某些超參數，估計器是過擬合還是欠擬合。

validation_score函數可以應用在該例子中：

>>> import numpy as np
>>> from sklearn.model_selection import validation_curve
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import Ridge

>>> np.random.seed(0)
>>> X, y = load_iris(return_X_y=True)
>>> indices = np.arange(y.shape[0])
>>> np.random.shuffle(indices)
>>> X, y = X[indices], y[indices]

>>> train_scores, valid_scores = validation_curve(Ridge(), X, y, "alpha",
...                                               np.logspace(-7, 3, 3),
...                                               cv=5)
>>> train_scores
array([[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
       [0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
       [0.51..., 0.52..., 0.49..., 0.47..., 0.49...]])
>>> valid_scores
array([[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
       [0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
       [0.46..., 0.25..., 0.50..., 0.49..., 0.52...]]) 

如果訓練分數和驗證分數都很低，估計器就是欠擬合。如果訓練集的分數很高，并且驗證集的分數很低，估計器就是過擬合。除此以外，估計器的效果就很好。一個較低的訓練分數和一個較高的驗證分數通常是不可能的。所有三個例子中可以在下圖中發現，通過指定不同的支持向量機（SVM）的參數在數字集上的結果。

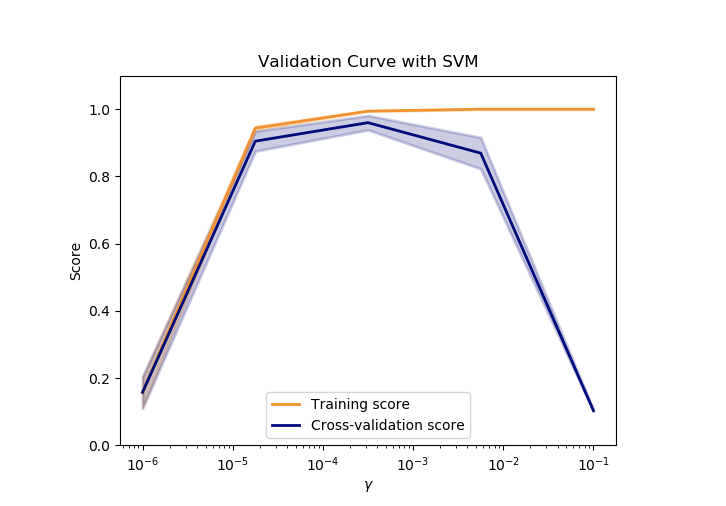
3.5.2 學習曲線

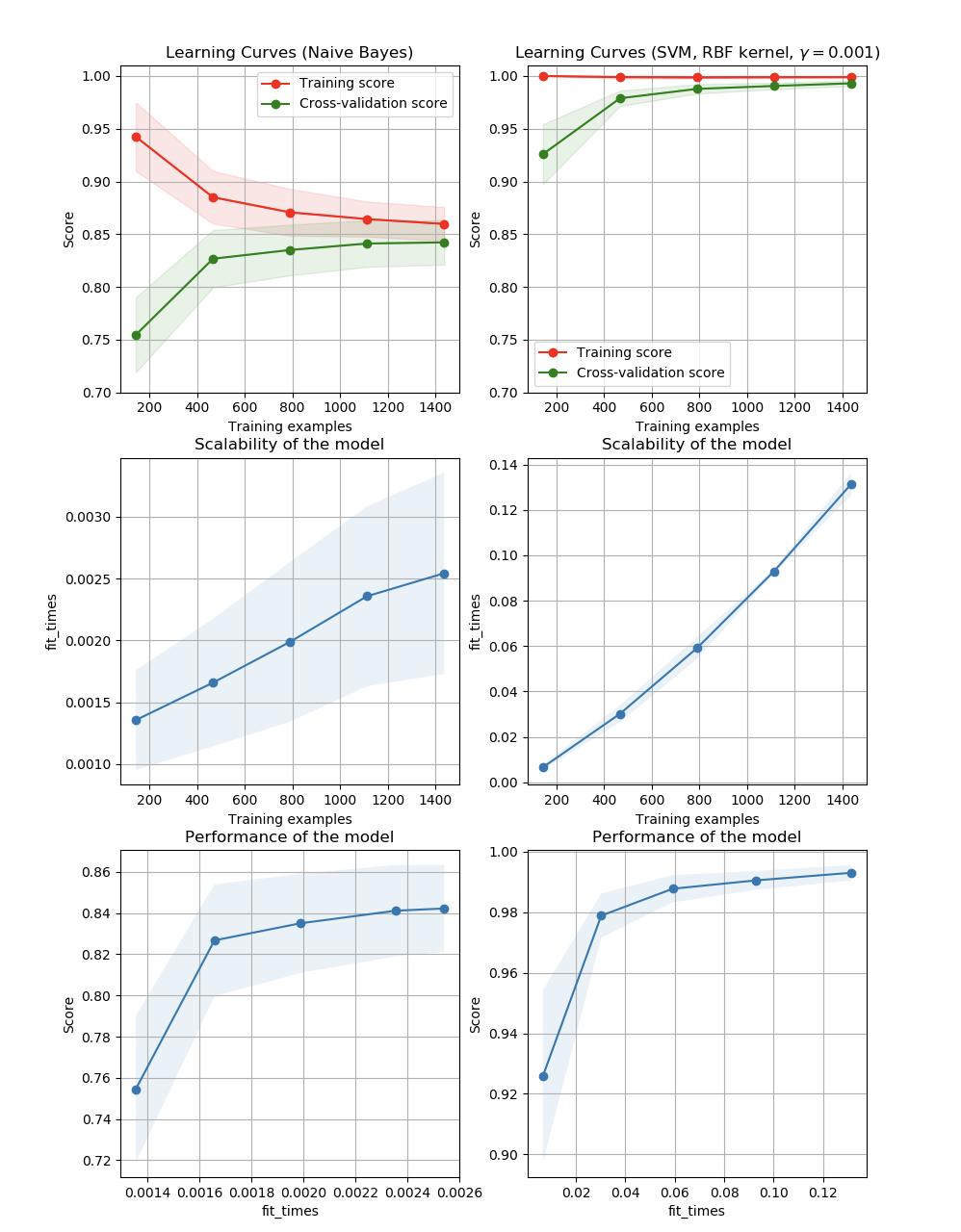
一個學習曲線表現的是在不同的訓練樣本個數下估計器的驗證集和訓練集得分。它是一個用于發現增加訓練集數據可以獲得多大收益和是否估計器會遭受更多的方差和偏差。考慮下面的例子中，繪制了樸素貝葉斯分類器和支持向量機的學習曲線。

對于樸素貝葉斯，驗證分數和訓練分數都向某一個分數收斂，隨著訓練集大小的增加，分數下降的很低。因次，并不會從較大的數據集中獲益很多。

與之相對比，小數據量的數據，支持向量機的訓練分數比驗證分數高很多。添加更多的數據給訓練樣本很可能會提高模型的泛化能力。

通過使用函數learning_curve繪制學習曲線所需的值（樣本被用的個數，訓練集的平均分數和驗證集的平均分數）：

>>> from sklearn.model_selection import learning_curve
>>> from sklearn.svm import SVC

>>> train_sizes, train_scores, valid_scores = learning_curve(
...     SVC(kernel='linear'), X, y, train_sizes=[50, 80, 110], cv=5)
>>> train_sizes
array([ 50, 80, 110])
>>> train_scores
array([[0.98..., 0.98 , 0.98..., 0.98..., 0.98...],
       [0.98..., 1.   , 0.98..., 0.98..., 0.98...],
       [0.98..., 1.   , 0.98..., 0.98..., 0.99...]])
>>> valid_scores
array([[1. ,  0.93...,  1. ,  1. ,  0.96...],
       [1. ,  0.96...,  1. ,  1. ,  0.96...],
       [1. ,  0.96...,  1. ,  1. ,  0.96...]])