2.6. 協方差估計?

許多統計問題都需要估計總體的協方差矩陣，這可以看作是對數據集散點圖形狀的估計。在大多數情況下，必須對某個樣本進行這樣的估計，其屬性（大小，結構，均勻性）對估計質量有很大影響。 sklearn.covariance包提供了用于在各種設置下準確估計總體協方差矩陣的工具。

我們假設觀測值是獨立的，并且分布相同（iid）。

2.6.1. 經驗協方差

已知數據集的協方差矩陣可以由經典的最大似然估計器(或“經驗協方差”)很好地近似，前提是觀測的數量要比特征的數量（描述觀測的變量）大得多。更準確地說，更準確地說，樣本的最大似然估計是相應總體協方差矩陣的無偏估計。

樣本的經驗協方差矩陣可以使用empirical_covariance包的功能來計算 ，或者使用 EmpiricalCovariance.fit方法將對象EmpiricalCovariance 與數據樣本擬合 。請注意，結果取決于數據是否聚集，因此可能需要準確的使用assume_centered參數。更準確地說，如果要使用 assume_centered=False，則假定測試集具有與訓練集相同的均值向量。如果不是，則兩者都應被用戶聚集后，再使用assume_centered=True。

示例：

2.6.2. 收縮協方差

2.6.2.1. 基本收縮

盡管最大似然估計是協方差矩陣的無偏估計，但它并不是對協方差矩陣特征值的一個良好的估計，因此從其反演中獲得的精度矩陣并不準確。有時，由于數值原因甚至會發生經驗協方差矩陣而無法反轉的情況。為了避免這種反演問題，引入了經驗協方差矩陣的一種變換方式：shrinkage。

在scikit-learn中，可以使用該方法將轉換（具有用戶定義的收縮系數）直接應用shrunk_covariance預先計算協方差。此外，協方差的收縮估計可以通過 ShrunkCovariance 對象的 ShrunkCovariance.fit方法擬合到數據中。同樣，結果取決于數據是否聚集，因此可能需要準確的使用參數assume_centered。

選擇收縮量， 相當于設置了偏差/方差權衡，下面將就此進行討論。

示例：

2.6.2.2. Ledoit-Wolf 收縮

O. Ledoit和M. Wolf 在他們2004年的論文[1]中提出了計算最佳收縮系數α的公式 。這樣可以使估計協方差矩陣與實際協方差矩陣之間的均方誤差最小。

可以使用sklearn.covariance包中 ledoit_wolf 函數來計算樣本的協方差的Ledoit-Wolf 估計， 或者擬合一個LedoitWolf對象對相同的樣本來獲取該估計。

注意：總體協方差矩陣是各向同性的情況

當樣本數量遠大于特征數量時，人們會認為沒有必要收縮。這背后的直覺是，如果總體協方差是滿秩的，則當樣本數量增加時，樣本協方差也將變為正定。結果，沒有必要收縮并且該方法應該自動進行收縮。

但是，當總體協方差恰好是單位矩陣的倍數時，在Ledoit-Wolf過程中就不是這種情況。在這種情況下，隨著樣本數量的增加，Lodoit-Wolf收縮率估算值接近1。這表明在Ledoit-Wolf的意義上，協方差矩陣的最佳估計是同一性的倍數。由于總體協方差已經是單位矩陣的倍數，因此Ledoit-Wolf解的確是一個合理的估計。

示例:

參考文獻：

  • 1O. Ledoit and M. Wolf, “A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices”, Journal of Multivariate Analysis, Volume 88, Issue 2, February 2004, pages 365-411.

2.6.2.3. Oracle 近似收縮

在假設數據是高斯分布的前提下，Chen等人。[2]得出了一個旨在選擇收縮系數的公式，該公式產生的均方誤差比Ledoit和Wolf公式具有更小均方誤差的收縮系數。所得到的估計器被稱為協方差的 Oracle 收縮近似估計器。

可以使用sklearn.covariance 包中函數 oas 計算樣本協方差的OAS估計，或者可以通過將 OAS 對象擬合到相同的樣本來獲得該估計。

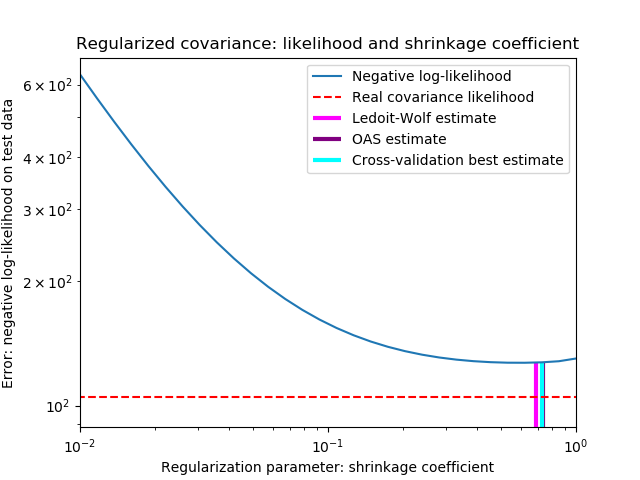設置收縮時的偏差-方差權衡:比較Ledoit-Wolf和OAS估計器的選擇

參考文獻:

[2]Chen et al., “Shrinkage Algorithms for MMSE Covariance Estimation”, IEEE Trans. on Sign. Proc., Volume 58, Issue 10, October 2010.

示例：

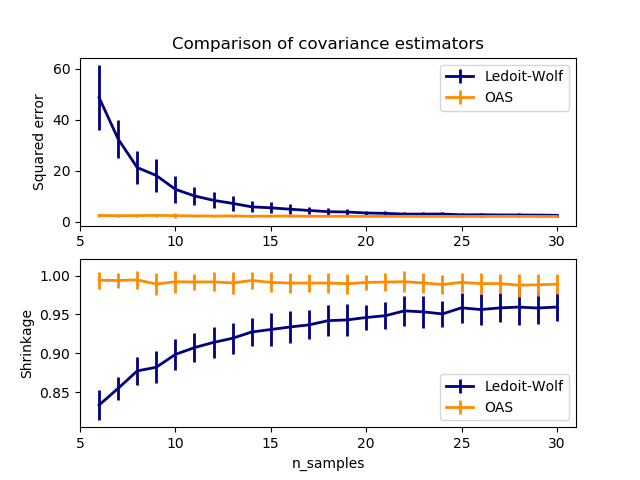
-見收縮協方差估計：LedoitWolf vs OAS和最大似然對于如何擬合OAS對象到數據。

-見Ledoit-Wolf vs OAS估計器，以可視化LedoitWolf還有一個OAS協方差的估計量。

2.6.3. 稀疏逆協方差

協方差矩陣的矩陣逆（通常稱為精度矩陣）與部分相關矩陣成正比。它給出了部分獨立性的關系。換句話說，如果兩個特征在條件上彼此獨立，則精度矩陣中的相應系數將為零。這就是為什么估計稀疏精度矩陣是有道理的：通過從數據中學習獨立關系，可以得到更好地調節協方差矩陣的條件。這稱為協方差選擇。

在小樣本情況下（n_samples和n_features相等或更小），稀疏的逆協方差估計量往往比收縮的協方差估計更好。但是，在相反的情況下，或者對于非常相關的數據，它們可能在數值上不穩定。另外，與收縮估計器不同，稀疏估計器能夠恢復非對角線結構。

GraphicalLasso估計器使用L1懲罰執行關于精度矩陣的稀疏性：alpha參數越高，精度矩陣越稀疏。相應的GraphicalLassoCV對象使用交叉驗證來自動設置alpha參數。

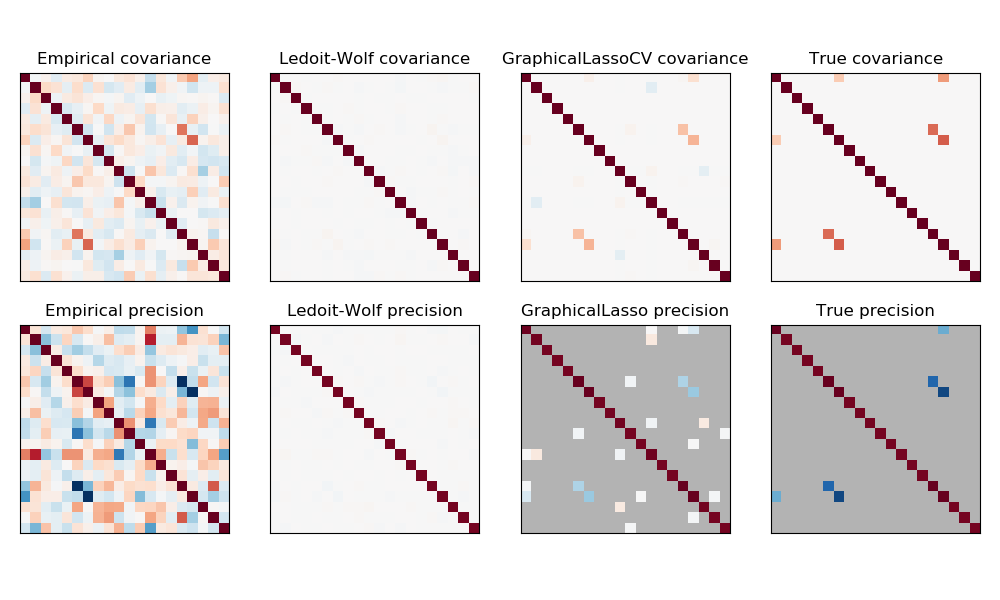協方差矩陣和精度矩陣基于最大似然度估計,收縮估計和稀疏估計的比較。

注意 ：結構恢復

從數據的相關性中恢復圖形結構是一項具有挑戰性的工作。如果您對這種恢復感興趣，請記住：

  • 從相關矩陣進行的恢復要比協方差矩陣容易：在運行 GraphicalLasso之前先對觀察值進行標準化
  • 如果底層圖的節點連接數比平均節點數多，則該算法將丟失其中一些連接。
  • 如果與基礎圖形中的邊數相比，觀察的次數不多，則將無法恢復。
  • 即使您處于良好的恢復條件下，通過交叉驗證（例如，使用GraphicalLassoCV對象）選擇的alpha參數 也會導致選擇過多的邊。但是，相關邊的權重將比無關邊大。

數學公式如下：

?

其中：是要估計的精度矩陣（precision matrix），是樣本的協方差矩陣。是非對角系數 的絕對值之和。 用于解決這個問題的算法是來自 Friedman 2008 Biostatistics 論文的 GLasso 算法。 它與 R 語言 glasso 包中的算法相同。

示例：

參考文獻：

2.6.4. 魯棒協方差估計

真實的數據集經常受到測量或記錄誤差的影響。由于各種原因，常規但不尋常的觀察也可能出現。罕見的觀測稱為異常值。上面顯示的經驗協方差估計器和收縮協方差估計器對數據中異常值的存在非常敏感。因此，應該使用魯棒的協方差估計器來估計實際數據集的協方差。 或者，可以使用魯棒協方差估計器來執行異常值檢測， 并根據數據的進一步處理:丟棄/降低某些觀察值。

該sklearn.covariance程序包實現了一個強大的協方差估計器，即最小協方差行列式[3]。

2.6.4.1. 最小協方差決定

最小協方差估計器是PJ Rousseeuw在[3]引入的數據集協方差的魯棒估計器。這個想法是找出一個給定比例（h）的 “良好” 觀察值，它們不是離群值， 然后計算他們的經驗協方差矩陣，以補償觀測值的執行選擇（“一致性步驟”）。 然后將該經驗協方差矩陣重新縮放以補償所執行的觀察選擇（”consistency step(一致性步驟)”）。計算完最小協方差決定估計器后，可以根據其馬氏距離（Mahalanobis distance）給出觀測值的權重, 得到數據集的協方差矩陣的重新加權估計（”reweighting step(重新加權步驟)”）。

Rousseeuw 和 Van Driessen [4]開發了 FastMCD 算法，以計算最小協方差決定因子。在 scikit-learn 中，在將 MCD 對象擬合到數據時, 使用該算法。FastMCD 算法同時計算數據集位置的魯棒估計。

原始估計(Raw estimates)可通過 MinCovDet 對象的 raw_location_ 和 raw_covariance_ 屬性獲得。

參考文獻：

  • [3] P. J. Rousseeuw. Least median of squares regression. J. Am Stat Ass, 79:871, 1984.
  • [4] A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS.

示例：

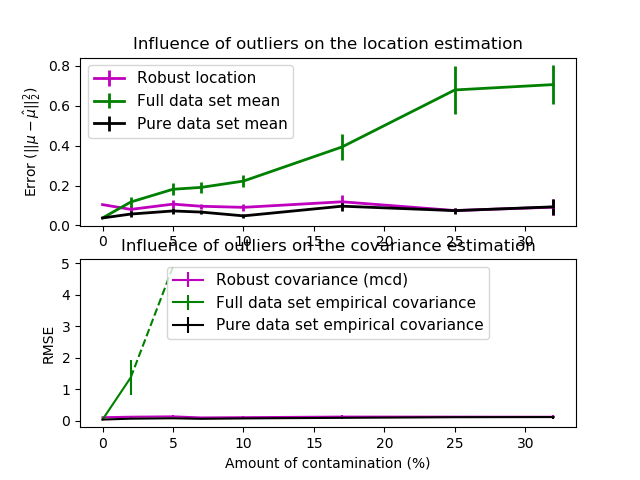
異常值對位置和協方差估計的影響 使用Mahalanobis距離分離內圍點和離群點

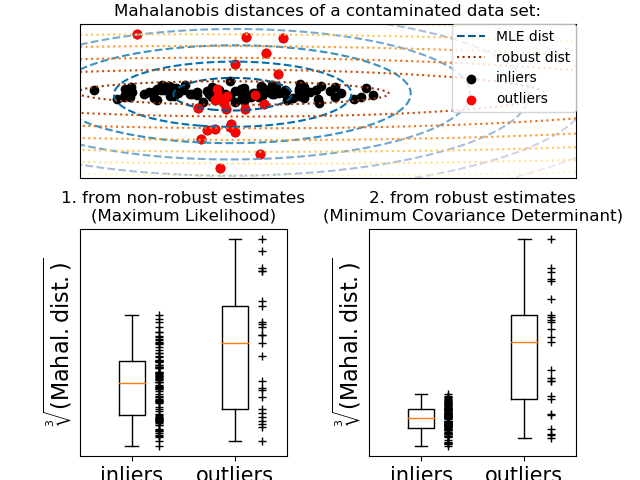異常值對位置和協方差估計的影響 使用Mahalanobis距離分離內圍點和離群點