置換重要性與隨機森林特征重要性(MDI)?

在這個例子中，我們將比較隨機RandomForestClassifier的基于不純的的特征重要性和使用permutation_importance在titanic數據集上的排列重要性。我們將證明基于不純度的特征重要性可以夸大數值特征的重要性。

此外，基于不純度的隨機森林特征重要性受到從訓練數據集得出的統計數據的影響：即使對于無法預測目標變量的特征，其重要性也可能很高，只要模型有能力使用它們來過度擬合。

此示例演示如何使用置換重要性作為可以減輕這些限制的替代方法。

References:

[1] L. Breiman, “Random Forests”, Machine Learning, 45(1), 5-32,

https://doi.org/10.1023/A:1010933404324

print(__doc__)
import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import fetch_openml
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.inspection import permutation_importance
from sklearn.compose import ColumnTransformer
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder

數據加載與特征工程

讓我們用pandas來加載泰坦尼克號數據集的副本。下面展示了如何對數值特征和分類特征分別進行預處理。

我們還包括兩個與目標變量(survived)沒有任何關聯的隨機變量：

random_num是一個高基數的數值變量(與記錄一樣多的唯一值)
random_cat是一個低基數的分類變量(3個可能的值)。

X, y = fetch_openml("titanic", version=1, as_frame=True, return_X_y=True)
rng = np.random.RandomState(seed=42)
X['random_cat'] = rng.randint(3, size=X.shape[0])
X['random_num'] = rng.randn(X.shape[0])

categorical_columns = ['pclass', 'sex', 'embarked', 'random_cat']
numerical_columns = ['age', 'sibsp', 'parch', 'fare', 'random_num']

X = X[categorical_columns + numerical_columns]

X_train, X_test, y_train, y_test = train_test_split(
    X, y, stratify=y, random_state=42)

categorical_pipe = Pipeline([
    ('imputer', SimpleImputer(strategy='constant', fill_value='missing')),
    ('onehot', OneHotEncoder(handle_unknown='ignore'))
])
numerical_pipe = Pipeline([
    ('imputer', SimpleImputer(strategy='mean'))
])

preprocessing = ColumnTransformer(
    [('cat', categorical_pipe, categorical_columns),
     ('num', numerical_pipe, numerical_columns)])

rf = Pipeline([
    ('preprocess', preprocessing),
    ('classifier', RandomForestClassifier(random_state=42))
])
rf.fit(X_train, y_train)

模型的精度

在檢驗特征重要性之前，重要的是要檢查模型的預測性能是否足夠高。事實上，我們對檢查非預測模型的重要特征沒有興趣。

在這里可以觀察到，訓練的精度很高(隨機森林模型有足夠的能力完全記住訓練集)，但是由于隨機森林的內置bagging，它仍然可以很好地推廣到測試集。

也許可以通過限制樹的容量(例如設置min_samples_leaf=5或者min_samples_leaf=10)來交換訓練集的一些準確性，從而在不引入太多不適當的情況下限制過度擬合。

然而，讓我們現在保持我們的高容量隨機森林模型，以說明一些具有特性重要性的陷阱，對于具有許多唯一值的變量:

print("RF train accuracy: %0.3f" % rf.score(X_train, y_train))
print("RF test accuracy: %0.3f" % rf.score(X_test, y_test))

RF train accuracy: 1.000
RF test accuracy: 0.817

從平均不純度減少(MDI)看樹的特征重要性

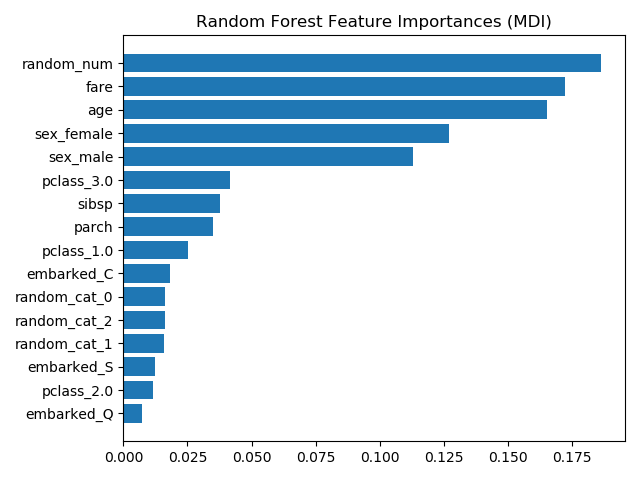
基于不純度的特征重要性將數值特征列為最重要的特征。因此，非預測的 random_num 變量是最重要的！

這個問題源于基于不純度的特征重要性的兩個限制

基于不純度的重要性傾向于高基數(取值很多)特征；
基于不純度的重要性是根據訓練集統計量計算的，因此不能反映特征的能力，從而無法進行泛化到測試集的預測(當模型有足夠的能力時)。

ohe = (rf.named_steps['preprocess']
         .named_transformers_['cat']
         .named_steps['onehot'])
feature_names = ohe.get_feature_names(input_features=categorical_columns)
feature_names = np.r_[feature_names, numerical_columns]

tree_feature_importances = (
    rf.named_steps['classifier'].feature_importances_)
sorted_idx = tree_feature_importances.argsort()

y_ticks = np.arange(0, len(feature_names))
fig, ax = plt.subplots()
ax.barh(y_ticks, tree_feature_importances[sorted_idx])
ax.set_yticklabels(feature_names[sorted_idx])
ax.set_yticks(y_ticks)
ax.set_title("Random Forest Feature Importances (MDI)")
fig.tight_layout()
plt.show()

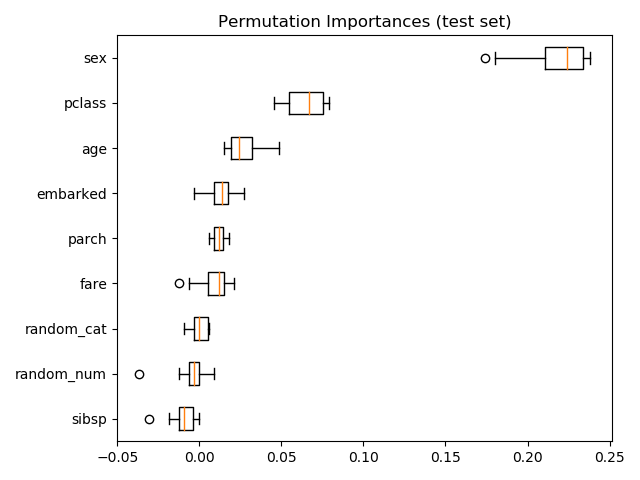
作為另一種選擇，rf的置換重要性是在一個在測試集上計算的。這說明基數低的分類特征，sex是最重要的特征。

還要注意的是，這兩個隨機特征的重要性都很低(接近0)。

result = permutation_importance(rf, X_test, y_test, n_repeats=10,
                                random_state=42, n_jobs=2)
sorted_idx = result.importances_mean.argsort()

fig, ax = plt.subplots()
ax.boxplot(result.importances[sorted_idx].T,
           vert=False, labels=X_test.columns[sorted_idx])
ax.set_title("Permutation Importances (test set)")
fig.tight_layout()
plt.show()

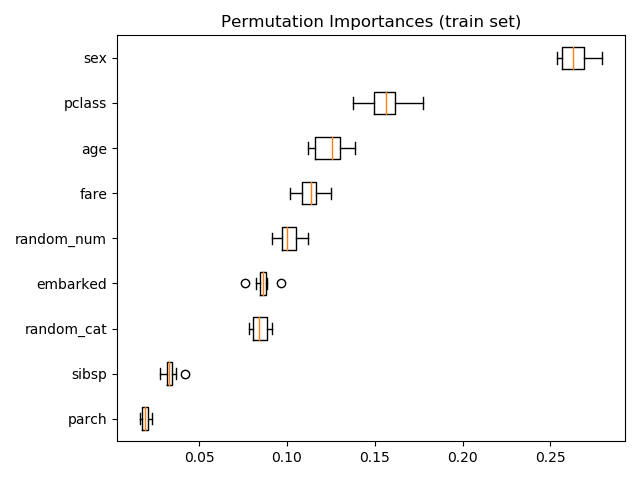
還可以計算訓練集上的置換重要性。這表明，與在測試集上計算時相比， random_num 獲得了更高的重要性排序。這兩幅圖的不同之處在于證實了RF模型有足夠的能力利用隨機數值特征來過度擬合。您可以通過以下方法進一步確認這一點：使用帶有 min_samples_leaf=10的受限 RF 重新運行此示例。

result = permutation_importance(rf, X_train, y_train, n_repeats=10,
                                random_state=42, n_jobs=2)
sorted_idx = result.importances_mean.argsort()

fig, ax = plt.subplots()
ax.boxplot(result.importances[sorted_idx].T,
           vert=False, labels=X_train.columns[sorted_idx])
ax.set_title("Permutation Importances (train set)")
fig.tight_layout()
plt.show()

腳本的總運行時間：(0分6.657秒)

Download Python source code: plot_permutation_importance.py

Download Jupyter notebook: plot_permutation_importance.ipynb