用鄰域成分分析進行降維?

用于降維的鄰域成分分析的樣本案例。

本案例比較了應用于手寫數字數據集的不同的（線性）降維方法。數據集包含從0到9的數字圖像，每個類別大約有180個樣本。每個圖像的尺寸為8x8 = 64，在這里我們將其縮小為二維數據點。

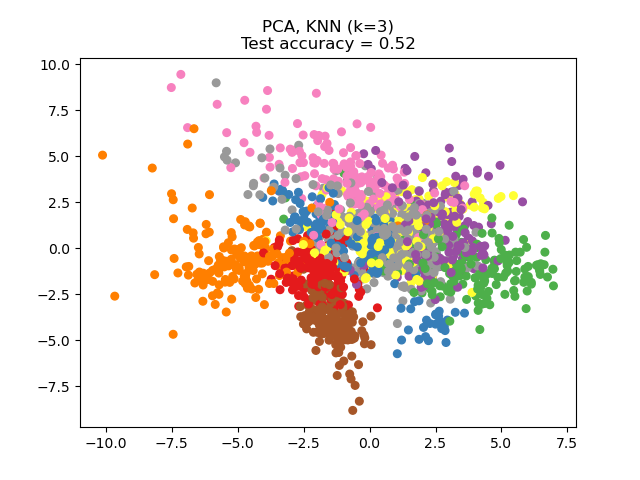
應用于此數據的主成分分析（PCA）可以識別出說明數據差異最大的特征組合（又被稱為主成分或特征空間中的方向）。在這里，我們在2個第一主成分上繪制了不同的樣本。

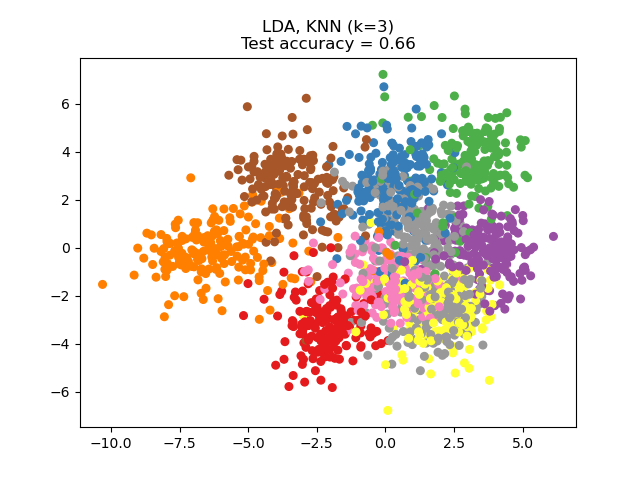
線性判別分析（LDA）嘗試識別出類別之間差異最大的屬性。尤其是，與PCA相比，LDA是使用已知類別標簽的受監督方法。

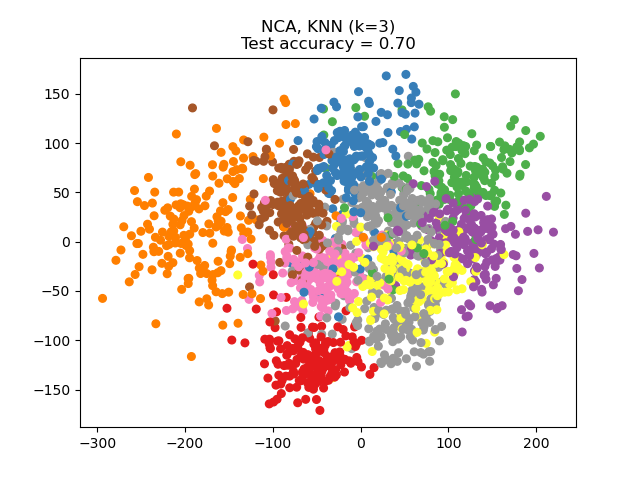
鄰域成分分析（NCA）試圖找到一個特征空間，以使隨機最近鄰算法具有最佳準確性。像LDA一樣，它是一種受監督的方法。

可以看到，盡管維數大大減少，但NCA還是對數據進行了聚類，這在視覺上是有意義的。

輸入：

# 執照: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neighbors import (KNeighborsClassifier,
                               NeighborhoodComponentsAnalysis)
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

print(__doc__)

n_neighbors = 3
random_state = 0

# 導入手寫數字數據集
X, y = datasets.load_digits(return_X_y=True)

# 分類訓練集與測試集
X_train, X_test, y_train, y_test = \
    train_test_split(X, y, test_size=0.5, stratify=y,
                     random_state=random_state)

dim = len(X[0])
n_classes = len(np.unique(y))

# 使用PCA將維度降到2維
pca = make_pipeline(StandardScaler(),
                    PCA(n_components=2, random_state=random_state))

# 使用LinearDiscriminantAnalysis將維度減小到2維
lda = make_pipeline(StandardScaler(),
                    LinearDiscriminantAnalysis(n_components=2))

# 使用NeighbourhoodComponentAnalysis將維度減小到2維
nca = make_pipeline(StandardScaler(),
                    NeighborhoodComponentsAnalysis(n_components=2,
                                                   random_state=random_state))

# 使用最近鄰分類器
knn = KNeighborsClassifier(n_neighbors=n_neighbors)

# 列出需要比較的方法
dim_reduction_methods = [('PCA', pca), ('LDA', lda), ('NCA', nca)]

# plt.figure()
for i, (name, model) in enumerate(dim_reduction_methods):
    plt.figure()
    # plt.subplot(1, 3, i + 1, aspect=1)

    # 擬合模型
    model.fit(X_train, y_train)

    # 在嵌入式訓練集上擬合最近鄰分類器
    knn.fit(model.transform(X_train), y_train)

    # 計算嵌入式測試集上的最近鄰精度
    acc_knn = knn.score(model.transform(X_test), y_test)

    # 使用擬合模型將數據集嵌入2維
    X_embedded = model.transform(X)

    # 繪制預測點并顯示評估分數
    plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=y, s=30, cmap='Set1')
    plt.title("{}, KNN (k={})\nTest accuracy = {:.2f}".format(name,
                                                              n_neighbors,
                                                              acc_knn))
plt.show()

腳本的總運行時間：（0分鐘2.546秒）