sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis?

class sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis(*, priors=None, reg_param=0.0, store_covariance=False, tol=0.0001)

[源碼]

二次判別分析

利用貝葉斯規則，對數據擬合類條件密度，生成一個二次決策邊界的分類器。

該模型對每個類都擬合一個高斯密度。

0.17版本新增：QuadraticDiscriminantAnalysis。

更多信息請參閱用戶指南。

參數	說明
priors	ndarray of shape (n_classes, ), default = None 類先驗。默認情況下，類的比例是由測試集推斷而來。
reg_param	float, default = 0.0 通過將S2轉換為`S2 = (1 - reg_param) * S2 + reg_param * np.eye(n_features)`來規范化每個類的協方差估計，其中S2對應于給定類的`scaling_`屬性。
store_convariance	bool, default = False 若為真，若為真，該類的協方差矩陣會被明確計算并保存至`self.covariance_`屬性中。 0.17版本新增內容
tol	float, default = 1.0e-4 我們認為利用奇異值的絕對閾值來估計Xk的秩是顯著的，其中Xk是類k中樣本的中心矩陣。該參數不影響預測。它只負責控制當特征被認為是共線時，發出警告。 0.17版本新增內容

屬性	說明
covariance_	list of len n_classes of ndarray of shape (n_features, n_features) 對于每個類，給出用該類樣本估計的協方差矩陣。估計是無偏的。只有當`store_covariance` = True時才會出現
means_	array-like of shape (n_classes, n_features) "類"均值。
priors_	array_like of shape (n_classes,) 類先驗(和為1)。
rotations_	list of len n_classes of ndarray of shape (n_features, n_k) 對于每個結構為(n_features, n_k)的類k，其中`n_k = min(n_features, 類k中的元素個數)`。它是高斯分布的旋轉，即其主軸。它對應于`V`，特征向量的矩陣來自于`Xk = U S Vt`的SVD，其中`Xk`是k類樣本的中心矩陣。
scalings_	list of len n_classses of ndarray of shape (n_k, ) 每一類都包含了高斯分布沿其主軸的縮放，即旋轉坐標系中的方差。對應`S^2 / (n_samples - 1)`，其中`S`為`Xk`的SVD奇異值的對角矩陣，`Xk`為類k樣本的中心矩陣。
classes_	ndarray of shape (n_classes, ) 唯一類標簽。

另見：

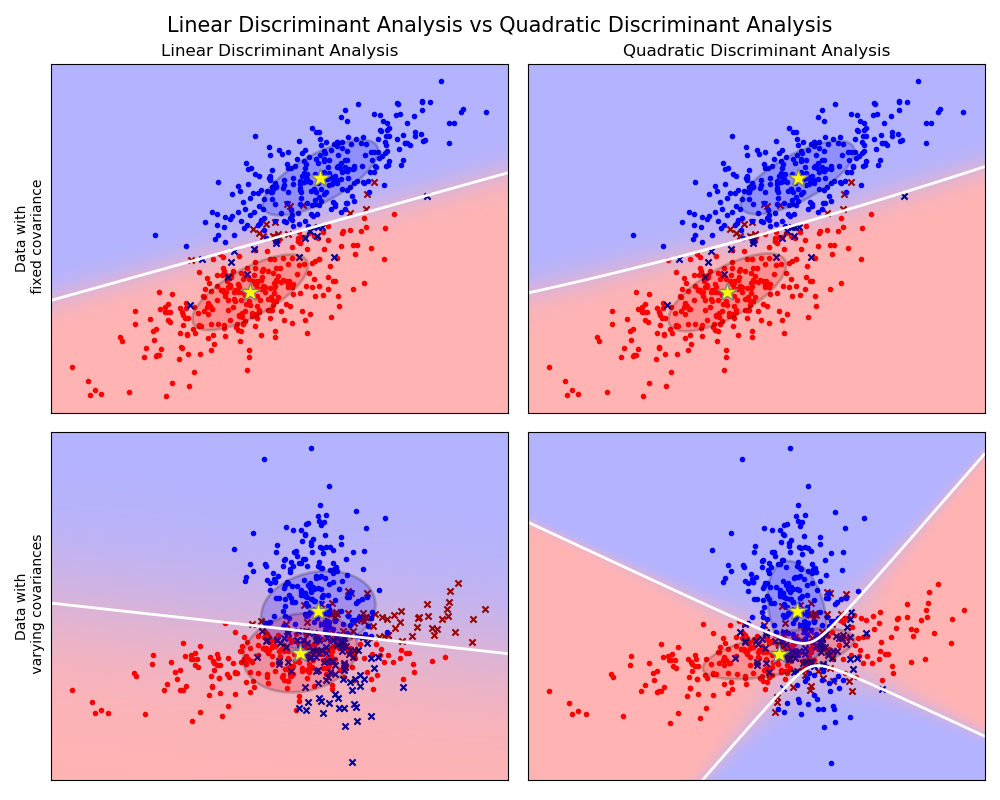
sklearn.discriminant_analysis.LinearDiscriminantAnalysis

線性判別分析

實例

>>> from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = QuadraticDiscriminantAnalysis()
>>> clf.fit(X, y)
QuadraticDiscriminantAnalysis()
>>> print(clf.predict([[-0.8, -1]]))
[1]

方法

方法	說明
`decision_function`(self, X)	對一個樣本數組應用決策函數
`fit`(self, X, y)	擬合數據然后將其進行轉化
`get_params`(self[, deep])	獲取當前估計量的參數
`predict`(self, X)	預測X中的樣本類型標簽
`predict_log_proba`(self, X)	返回分類的對數后驗概率
`predict_proba`(self, X)	返回分類的后驗概率
`score`(self, X, y[, sample_weight])	返回給定測試數據及標簽的精確度均值
`set_params`(self, **params)	設置該估計量的參數

__init__(self, *, priors=None, reg_param=0.0, store_covariance=False, tol=0.0001)

[源碼]

初始化self。請參閱help(type(self))以獲得準確的說明。

decision_function(self, X)

[源碼]

對一個樣本數組應用決策函數。

決策函數等于(取決于一個常數向量)模型的對數后驗概率，也就是，log p(y = k | x)。在二元分類中，作出如下設置來對應區別。log p(y = 1 | x) - log p(y = 0 | x)。參見 LDA和QDA分類器的數學公式。

參數	說明
X	array-like of shape (n_samples, n_features) 樣本數組(測試向量)。

返回值	說明
C	ndarray of shape (n_samples,) or (n_sample, n_classes) 決策函數值與每個類、樣本相關。在二分類的樣例中，樣本大小為(n_samples, )，給出正類的對數似然比。

fit(self, X, y)

[源碼]

根據給定的模型擬合LinearDiscriminantAnalysis模型

訓練數據及參數。

0.19版本更變：store_covariance被移至主要構造函數

? tol被移至主要構造函數

參數	說明
X	array-like of shape (n_samples, n_features) 訓練數據
y	array-like of shape (n_sample, ) 目標值

get_params(self, deep=True)

[源碼]

獲取當前估計量的參數。

參數	說明
deep	bool, default = True 如果為真，則將返回此估計量和作為估計量的所包含子對象的參數

返回值	說明
params	mapping of string to any 參數名被映射至他們的值

predict(self, X)

[源碼]

預測X中的樣本類型標簽。

參數	說明
X	array_like or sparse matrix, shape (n_samples, n_features) 樣本

返回值	說明
C	array, shape [n_samples] 每個樣本所獲得預測的分類標簽

predict_log_proba(self, X)

[源碼]

返回分類的對數后驗概率。

參數	說明
X	array-like of shape (n_sample, n_features) 數組樣本或測試向量

返回值	說明
C	ndarray of shape (n_sample, n_classes) 各類的分類對數后驗概率

predict_proba(self, X)

[源碼]

估計概率

參數	說明
X	array-like of shape (n_sample, n_features) 數組樣本或測試向量

返回值	說明
C	ndarray of shape (n_sample, n_classes) 各類的分類對數概率

score(self, X, y, sample_weight=None)

[源碼]

返回給定測試數據和標簽的平均精度。

在多標簽分類中，這是一個嚴格矩陣下的子集精度，因為你需要對每個樣本正確預測每個標簽集。

參數	說明
X	array-like of sshape (n_samples, nfeatures) 測試樣本
y	array-like of shape (n_sample, ) or (n_samples, n_outputs) X中結果為真的標簽

返回值	說明
score	float self.predict(X) wrt. y.的平均精度

set_params(self, **params)

[源碼]

設置當前估計量的參數。

該方法適用于簡單估計量和嵌套對象(如pipline)。后者具有形式為<component>__<parameter>的參數，這樣就讓更新嵌套對象的每個組件成為了可能。

參數	說明
f_params	dict 估計量參數

返回值	說明
self	object 估計量實例

sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis使用示例?

分類器的比較 ?

協方差橢球的線性和二次判別分析 ?