1.2 線性和二次判別分析?

線性判別分析(discriminant_analysis.LinearDiscriminantAnalysis) 和二次判別分析(discriminant_analysis.QuadraticDiscriminantAnalysis) 是兩種經典的分類器，如它們的名字所示，分別具有線性和二次決策平面。

這些分類器之所以有吸引力，是因為它們有一些的解析解，可以很容易地計算出，本質上是多分類的，在實踐中證明工作良好，并且沒有需要調優的超參數。

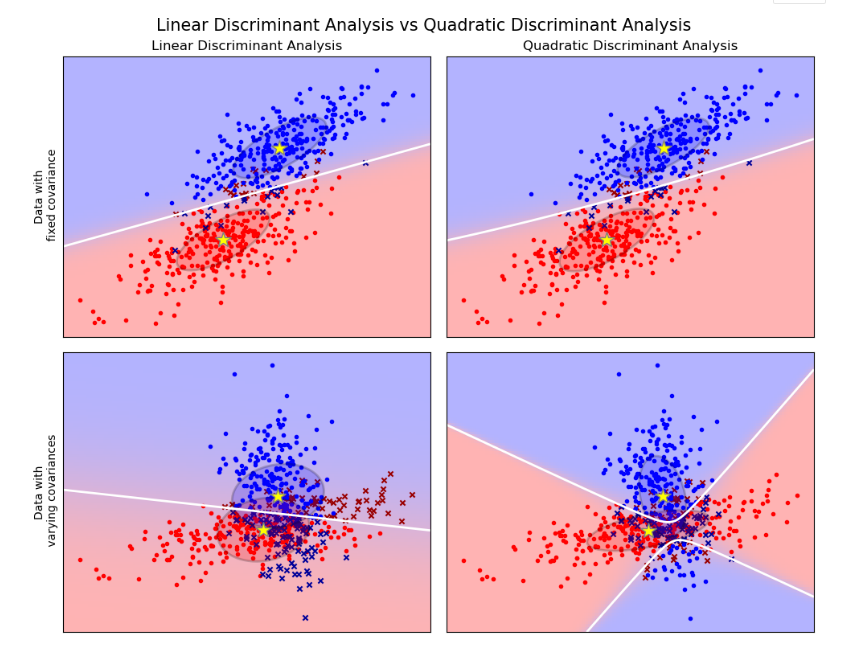
圖中給出了線性判別分析和二次判別分析的決策邊界。底部那行證明線性判別分析只能學習線性邊界，而二次判別分析可以學習二次邊界，因此具有更大的靈活性。

示例
協方差橢球的線性和二次判別分析LDA和QDA在人造數據上的比較

1.2.1.基于線性判別分析的降維方法

discriminant_analysis.LinearDiscriminantAnalysis 可用于執行有監督的降維，方法是將輸入數據投影到一個線性子空間，該空間由使類與類之間的分離最大化的方向組成(在下面的數學部分中討論的準確意義)。輸出的維數必然小于類的數量，因此，一般來說，這是一個相當強的降維，并且只有在多類設置中才有意義。

算法的實現是在discriminant_analysis.LinearDiscriminantAnalysis.transform，可以使用 n_components參數設置所需的維數。這個參數對discriminant_analysis.LinearDiscriminantAnalysis.fit或者 discriminant_analysis.LinearDiscriminantAnalysis.predict沒有影響。

示例
在lris數據集上比較LDA和PCA:基于lris數據集比較LDA和PCA的降維方法

1.2.2 LDA和QDA分類器的數學表達式

LDA和QDA都可以從簡單的概率模型中推導出來，這種概率模型模擬了每一類中的數據的條件分布

，然后，就可以利用貝葉斯公式進行預測：

我們選擇可以使得上述條件概率最大化的

。

更具體地說，對于線性和二次判別分析，

被建模為具有密度的多元高斯分布：

其中

是特征的數目。

1.2.2.1 QDA

根據上面的模型，后驗的對數為：

常數項

對應于分母

，以及其他來自高斯的常數項。預測類是使這種對數后驗最大化的類。

注意：與高斯樸素貝葉斯的關系
如果在QDA模型中，假設協方差矩陣是對角矩陣，在每個類中，輸入都是條件獨立的，那么所得到的分類器等價于高斯樸素貝葉斯分類器`naive_bayes.GaussianNB`。

1.2.2.2 LDA

LDA是QDA的特例，其中假設每個類別的高斯都共享相同的協方差矩陣：

(對所有

)。這將對數后驗減少到:

對應在樣本與均值樣品

之間的馬氏距離（Mahalanobis Distance）。馬氏距離表示距離均值的遠近程度，同時還要考慮每個特征的方差。因此，我們可以將LDA解釋為根據馬氏距離把分配給最接近平均值的類，同時也考慮了類的先驗概率。

LDA的對數后驗也可以寫為[3]：

and 。這些數量分別對應于coef_和intercept_屬性。

由上式可知，LDA具有一個線性決策曲面。對于QDA，沒有對協方差矩陣的高斯的假設，導致二次決策曲面。詳見 [1] 。

1.2.3 LDA降維的數學公式

首先請注意，表示是中的向量，并且導致產生至少個仿射子空間（2點在一條線上，3點在一條平面上，依此類推）。

如上所述，我們可以將LDA解釋為分配 x 對那些卑鄙的人 μk在最接近馬氏距離上最接近，同時也考慮了該類的先驗概率。或者，LDA等效于首先對數據進行球化處理，以使協方差矩陣為單位，然后分配x 以歐幾里得距離最接近均值（仍占先驗類）。

如上所述，我們可以將LDA解釋為分配給其在馬氏距離中是最接近均值的類，同時也考慮了類的先驗概率。或者，LDA等價于首先將數據球化，以協方差矩陣作為單位，然后根據歐氏距離分配最接近的平均值(仍然考慮類先驗)。

計算此維空間中的歐幾里得距離等同于首先將數據點投影到維空間中，然后計算距離（因為其他維度在距離方面將對每個類別均等地做出貢獻）。換句話說，如果在原始空間中最接近，情況也會如此。這說明，在LDA分類器中，通過線性投影到 K?1 維空間。

通過投影到線性子空間上，使得投影后的的方差最大化， (事實上，我們是對類的均值)做了主成分分析(PCA), 我們就能進一步的降維，知道達到。這個L對應于transform方法中使用的參數 n_components 。有關更多詳細信息，請參見 [1]。

1.2.4 收縮(Shrinkage)

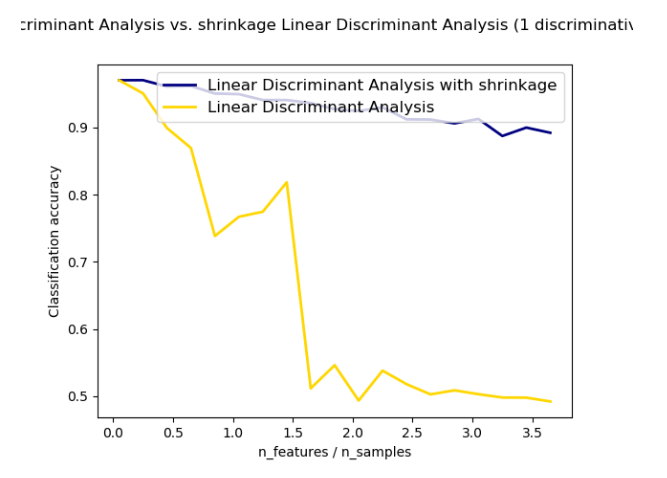
收縮(Shrinkage)是在訓練樣本數相對于特征數較少的情況下改進協方差矩陣估計的一種工具。在這種情況下，經驗樣本協方差是一個很差的預測器。Shrinkage LDA可以通過在 discriminant_analysis.LinearDiscriminantAnalysis中將參數shrinkage設置為‘auto’來使用。這里自動確定最優的Shrinkage的參數的方法主要是依據Ledoit and Wolf [4]中所提到的理論。注意， Shrinkage要想起作用，只有將參數 solver設置為 ‘lsqr’ or ‘eigen’。

shrinkage參數也可以手動設置在0到1之間。特別地是，0對應于沒有收縮(這意味著將使用經驗協方差矩陣)，而1對應于完全收縮(這意味著方差的對角矩陣將用作協方差矩陣的估計)。將此參數設置為這兩個極值之間的值將估計一個協方差矩陣的收縮版本。

1.2.5 預估算法

使用LDA和QDA需要計算后驗對數，這取決于類的先驗，該類表示以及協方差矩陣。

“ svd”求解器是用默認求解器 LinearDiscriminantAnalysis，并且是 QuadraticDiscriminantAnalysis唯一可用的求解器。它可以執行分類和轉換(對于LDA)。由于它不依賴于協方差矩陣的計算，“svd”求解器在特征數量較大的情況下可能更可取。'svd'求解器不能與收縮一起使用。SVD求解器的使用依賴于協方差矩陣 ,根據定義，等于

，來自（居中）矩陣的SVD：。事實證明，我們可以計算上面的對數后驗，而不必顯式計算：通過的SVD足夠計算 S 和 V 。對于LDA，將計算兩個 SVD：居中輸入矩陣的SVDX以及類均值向量的SVD。

“ lsqr”求解器是僅適用于分類的高效算法。它需要顯式計算協方差矩陣，并支持收縮。該求解器計算系數通過解決

，從而避免了對逆的顯式計算。

‘eigen’ 解決器是基于類散度與類內離散率之間的優化。它可以被用于分類以及轉換，此外它還同時支持收縮。然而該解決方案需要計算協方差矩陣，因此它可能不適用于具有大量特征的情況。

示例
正態和收縮線性判別分析在分類中的應用:帶收縮和不收縮LDA分類器的比較

參考資料：

1(1,2)“The Elements of Statistical Learning”, Hastie T., Tibshirani R., Friedman J., Section 4.3, p.106-119, 2008.
2Ledoit O, Wolf M. Honey, I Shrunk the Sample Covariance Matrix. The Journal of Portfolio Management 30(4), 110-119, 2004.
3R. O. Duda, P. E. Hart, D. G. Stork. Pattern Classification (Second Edition), section 2.6.2.