sklearn.discriminant_analysis.LinearDiscriminantAnalysis?
class sklearn.discriminant_analysis.LinearDiscriminantAnalysis(*, solver='svd', shrinkage=None, priors=None, n_components=None, store_covariance=False, tol=0.0001)
線性判別分析
利用貝葉斯規則對數據擬合類條件密度,生成具有線性判定邊界的分類器。
該模型對每個類擬合一個高斯密度,假設所有類有相同的協方差矩陣。
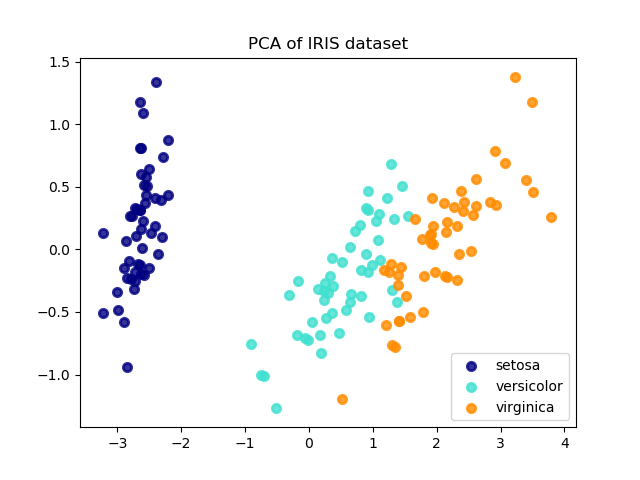
擬合模型還可以利用 transform方法將輸入投影到最具辨別力的方向,從而降低輸入的維數。
0.17版本新增:LinearDiscriminantAnalysis。
在用戶指南中獲取更多內容。
| 參數 | 說明 |
|---|---|
| solver | {"svd","lsqr","eigen"}, default = "svd" 解算器可能使用的值: ?"svd": 奇異值分解(默認)。不計算協方差矩陣,因此該解算器被推薦用于具有大量特征的數據。 ?"lsqr": 最小二乘解,能夠與收縮參數合并使用。 ?"eigen": 特征值分解,能夠與收縮參數合并使用。 |
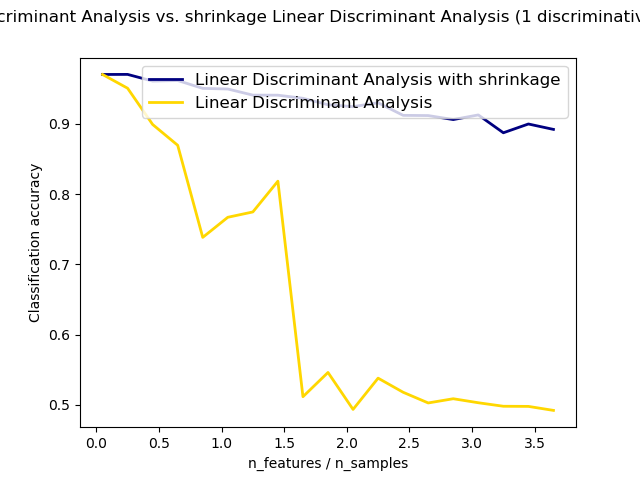
| shrinkage | "auto" or float,default = None 收縮參數可能使用的值: ?None: 無收縮(默認)。 ?"auto": 利用Ledoit-Wolf引理進行自動收縮。 ?float between 0 and1: 0 到 1 之間的修正收縮參數。 注意,收縮參數僅在"lsqr"和"eigen"解算器中有效。 |
| priors | Array_like of shape (n_classes,), default = None 先驗概率。默認情況下,類的比例是根據訓練集推斷出來的。 |
| n_components | int, default = None 降維所保留的成分個數(<= min(n_classed - 1, n_features))。如果為None,該值會賦予min(n_classes - 1, n_features)。該參數值會對變化方法產生影響。 |
| store_convariance | bool, default = False 若為真,當解算器為"svd"時,明確計算加權的類內協方差矩陣。不論真/假,其余兩種解算器的矩陣總是會被計算并儲存。 0.17版本新增。 |
| tol | float, default = 1.0e-4 對于X一個奇異值的絕對閾值,常常被用來估計X的秩,這種估計是顯著的。僅當解算器為"svd"時,不顯著的奇異值維度將會被舍棄。 0.17版本新增。 |
| 屬性 | 說明 |
|---|---|
| chef_ | ndarray of shape (n_features,) or (n_classes, n_features) 權重向量。 |
| intercept_ | ndarray of shape (n_classes,) 截距項。 |
| covariance_ | array-like of shape(n_features, n_features) 加權類內協方差矩陣。它對應于sum_k prior_k * C_k,其中C_k是k類樣本的協方差矩陣,同時它也是個估計量,來源于(可能縮小的)協方差的有偏估計。如果解算器為"svd",該矩陣僅在store_convariance = True的情況下存在。 |
| explained_variance_ratio_ | ndarray of shape (n_components,) 每個被選中成分所能解釋的方差的百分比。如果n_conponents這個參數沒有被設置,那么所有的成分都將被保存,同時所有解釋方差的累積之和會等于1。 該值只有在"eigen" 或"svd"兩解算器情況下可以得到。 |
| means_ | array-like of shape (n_classes, n_features) "類"均值。 |
| priors_ | array_like of shape (n_classes,) 類先驗(和為1)。 |
| scalings_ | array-like of shape (rank, n_classes - 1) 縮放特征存在于由類心所張成的空間之中。僅可以在解算器為"svd" 和"eigen"情況下獲得。 |
| xbar_ | array-like of shape (n_features,) 整體均值。只有在解算器為"svd"時,會予以展示。 |
| classes_ | array-like of shape (n_classes) 唯一類標簽。 |
另見:
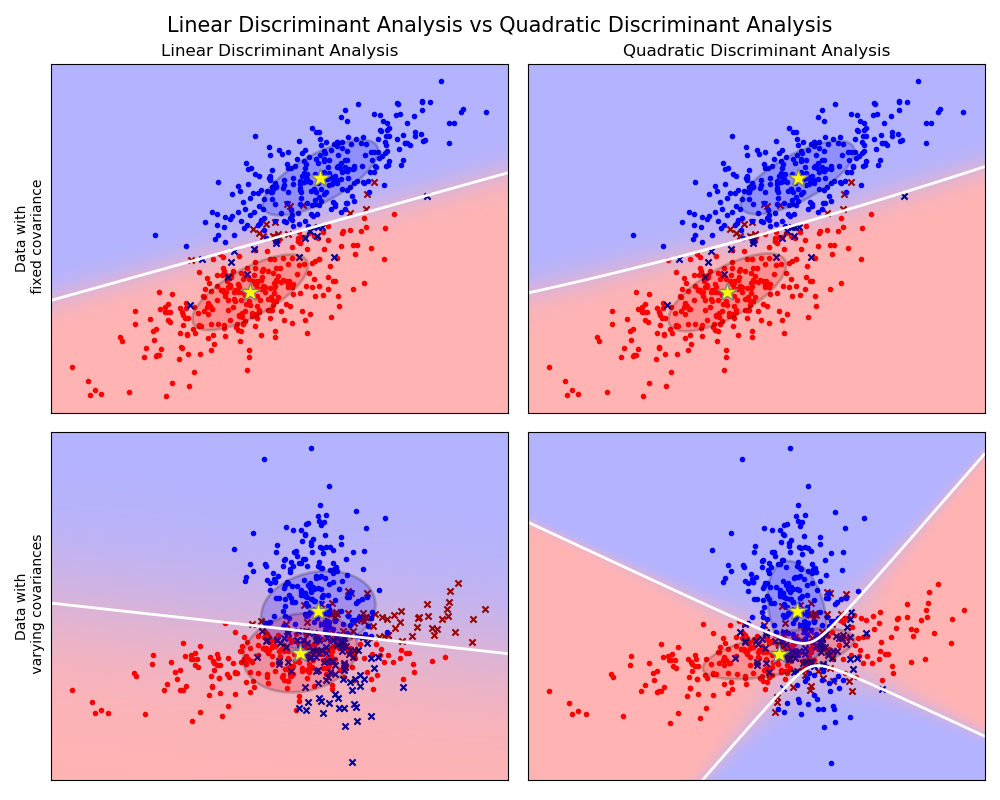
sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis二次判別分析
示例:
>>> import numpy as np
>>> from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = LinearDiscriminantAnalysis()
>>> clf.fit(X, y)
LinearDiscriminantAnalysis()
>>> print(clf.predict([[-0.8, -1]]))
[1]
方法
| 方法 | 說明 |
|---|---|
decision_function(self, X) |
將決策函數應用于樣本數組 |
fit(self, X, y) |
根據給定的模型擬合LinearDiscriminantAnalysis模型 |
fit_transform(self, X[, y]) |
擬合數據然后將其進行轉化 |
get_params(self[, deep]) |
獲取當前估計量的參數 |
predict(self, X) |
預測X中的樣本類型標簽 |
predict_log_proba(self, X) |
估計對數概率 |
predict_proba(self, X) |
估計概率 |
score(self, X, y[, sample_weight]) |
返回給定測試數據和標簽的平均精度 |
set_params(self, **params) |
設置當前估計量的參數 |
transform(self, X) |
將數據投射至最大類分塊中 |
__init__(self, *, solver='svd', shrinkage=None, priors=None, n_components=None, store_covariance=False, tol=0.0001)
初始化self。請參閱help(type(self))以獲得準確的說明。
decision_function(self, X)
對一個樣本數組應用決策函數。
決策函數等于(取決于一個常數向量)模型的對數后驗概率,也就是,log p(y = k | x)。在二元分類中,作出如下設置來對應區別。log p(y = 1 | x) - log p(y = 0 | x)。參見 LDA和QDA分類器的數學公式。
| 參數 | 說明 |
|---|---|
| X | array-like of shape (n_samples, n_features) 樣本數組(測試向量)。 |
| 返回值 | 說明 |
|---|---|
| C | ndarray of shape (n_samples,) or (n_sample, n_classes) 決策函數值與每個類、樣本相關。在二分類的樣例中,樣本大小為(n_samples, ),給出正類的對數似然比。 |
fit(self, X, y)
根據給定的模型擬合LinearDiscriminantAnalysis模型
訓練數據及參數。
0.19版本更變:store_covariance被移至主要構造函數
tol被移至主要構造函數
| 參數 | 說明 |
|---|---|
| X | array-like of shape (n_samples, n_features) 訓練數據 |
| y | array-like of shape (n_sample, ) 目標值 |
fit_transform(self, X, y=None, fit_params)
擬合數據然后將其進行轉化。
使用可選參數fit_params將轉換器擬合到X和y,并返回X的轉換值。
| 參數 | 說明 |
|---|---|
| X | {array-like, sparse matrix, dataframe} of shape (n_sample, n_features) |
| y | ndarray of shape (n_samples, ), default = None 目標值 |
| **fit_params | dict 附加擬合參數 |
| 返回值 | 說明 |
|---|---|
| X_new | ndarray array of shape (n_samples, n_features_new) 轉化后的數組 |
get_params(self, deep=True)
獲取當前估計量的參數
| 參數 | 說明 |
|---|---|
| deep | bool, default = True 如果為真,則將返回此估計器和其所包含子對象的參數 |
| 返回值 | 說明 |
|---|---|
| params | mapping of string to any 參數名被映射至他們的值 |
predict(self, X)
預測X中的樣本類型標簽。
| 參數 | 說明 |
|---|---|
| X | array_like or sparse matrix, shape (n_samples, n_features) 樣本 |
| 返回值 | 說明 |
|---|---|
| C | array, shape [n_samples] 每個樣本所獲得預測的分類標簽 |
predict_log_proba(self, X)
估計對數概率
| 參數 | 說明 |
|---|---|
| X | array-like of shape (n_sample, n_features) 輸入數據 |
| 返回值 | 說明 |
|---|---|
| C | ndarray of shape (n_sample, n_classes) 估計后的對數概率 |
predict_proba(self, X)
估計概率
| 參數 | 說明 |
|---|---|
| X | array-like of shape (n_sample, n_features) 輸入數據 |
| 返回值 | 說明 |
|---|---|
| C | ndarray of shape (n_sample, n_classes) 估計后的對數概率 |
score(self, X, y, sample_weight=None)
返回給定測試數據和標簽的平均精度。
在多標簽分類中,這是子集準確性,這是一個嚴格的指標,因為你需要對每個樣本正確預測每個標簽集。
| 參數 | 說明 |
|---|---|
| X | array-like of sshape (n_samples, nfeatures) 測試樣本 |
| y | array-like of shape (n_sample, ) or (n_samples, n_outputs) X中結果為真的標簽 |
| 返回值 | 說明 |
|---|---|
| score | float self.predict(X) wrt. y.的平均精度 |
set_params(self, **params)
設置當前估計量的參數。
該方法適用于簡單估計量和嵌套對象(如pipline)。后者具有形式為<component>_<parameter>的參數,這樣就讓更新嵌套對象的每個組件成為了可能。
| 參數 | 說明 |
|---|---|
| f_params | dict 估計量參數 |
| 返回值 | 說明 |
|---|---|
| self | object 估計器實例 |
transform(self, X)
將數據投射至最大類分塊中。
| 參數 | 說明 |
|---|---|
| X | array-like of shape (n_samples, n_features) 輸入數據 |
| 返回值 | 說明 |
|---|---|
| X_new | ndarray of shape (n_samples, n_features) 轉換后的數據 |