2.9. 神經網絡模型（無監督）?

2.9.1. 受限波爾茲曼機

受限玻爾茲曼機(RBM)是一種基于概率模型的無監督非線性特征學習器。當饋入線性分類器（如線性支持向量機或感知機）時，用 RBM 或多層次結構的RBM提取的特征時通常會獲得良好的結果。

該模型對輸入的分布做出假設。目前，scikit-learn 只提供了 BernoulliRBM，它假定輸入是二值的，或是 0 到 1 之間的值，每個值都編碼了特定特征被激活的可能性。

RBM嘗試使用特定的圖形模型來最大化數據的可似然。所使用的參數學習算法（隨機最大似然）可防止特征偏離輸入數據，從而使它們捕獲到特征有趣的規律性，但使模型對小型數據集的用處不大，通常不適用于密度估計。

該方法以初始化具有獨立RBM權重的深度神經網絡而廣受歡迎。這種方法稱為無監督預訓練。

示例：

  • [Restricted Boltzmann Machine features for digit classification](

2.9.1.1. 圖形模型和參數化

RBM 的圖形模型是一個全連接的二分圖。

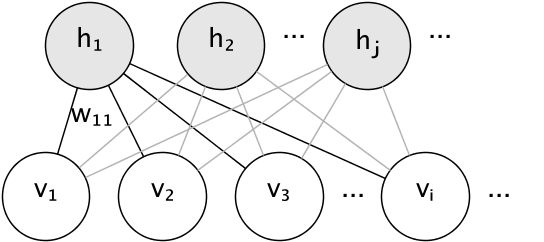節點是隨機變量，其狀態取決于它們連接到的其他節點的狀態。因此，通過連接的權重以及每個可見和隱藏單元的一個偏置項（截距）對模型進行參數化，為簡單起見，圖像中將其省略。

用能量函數衡量聯合概率分布的質量：

在上面的公式中 b 和 c分別是可見層和隱藏層的截距向量。該模型的聯合概率是根據能量定義的：

“限制”是指模型的二分圖結構，它禁止隱藏單元或可見單元之間的直接交互。這意味著假定以下條件獨立：

二分圖結構允許使用高效的塊Gibbs采樣進行推斷。

2.9.1.2. 伯努利受限玻爾茲曼機

在 BernoulliRBM 中，所有單位都是二進制隨機單元。這意味著輸入的數據應該是二值，或者是介于 0 和 1 之間的實數值，其表示可見單元將打開或關閉的可能性。這對于字符識別是一個很好的模型，因為我們感興趣的是哪些像素處于活動狀態，哪些像素未處于活動狀態。 對于自然場景的圖像，由于背景、深度和相鄰像素趨向于取相同的值，它不再適合。

每個單位的條件概率分布由其接收的輸入的 logistic sigmoid函數給出：

其中 是 logistic sigmoid函數：

2.9.1.3. 隨機最大似然學習

在 BernoulliRBM 函數中實現的訓練算法被稱為隨機最大似然（SML）或持續對比發散（PCD）。由于數據的似然函數的形式，直接優化最大似然是不可行的：

為簡單起見，上面的公式是針對單個訓練樣本編寫的相對于權重的梯度由與上述相對應的兩項構成。對應它們各自的符號，通常被稱為正梯度和負梯度。在該實施方式中，梯度是在樣本的小批量上估計的。

在最大化對數似然度的過程中，正梯度使得模型更傾向于與觀測到的訓練數據相容的隱藏狀態。由于RBMs 的二分體結構可以使它被高效地計算。然而，負梯度是棘手的。它的目標是降低模型偏好的聯合狀態的能量，從而使其與數據保持一致。它可以使用馬爾可夫鏈蒙特卡羅來通過Gibbs采樣粗略估計，它通過迭代地對每個 和 進行交互采樣，直到鏈混合。以這種方式產生的樣本有時被稱為幻想粒子。這是低效的，并且很難確定馬可夫鏈是否混合。

對比發散方法建議在經過少量迭代后停止鏈，迭代數 通常是 1。該方法速度快、方差小，但樣本遠離模型分布。

持續對比發散解決了這個問題。在 PCD 中，我們保留了多個鏈（幻想粒子）來在每個權重更新之后更新 個Gibbs采樣步驟，而不是每次需要梯度時都啟動一個新的鏈，并且只執行一個吉比斯采樣步驟。這使得粒子能更徹底地探索空間。

參考文獻;