sklearn.metrics.brier_score_loss?
sklearn.metrics.brier_score_loss(y_true, y_prob, *, sample_weight=None, pos_label=None)
計算Brier分數。
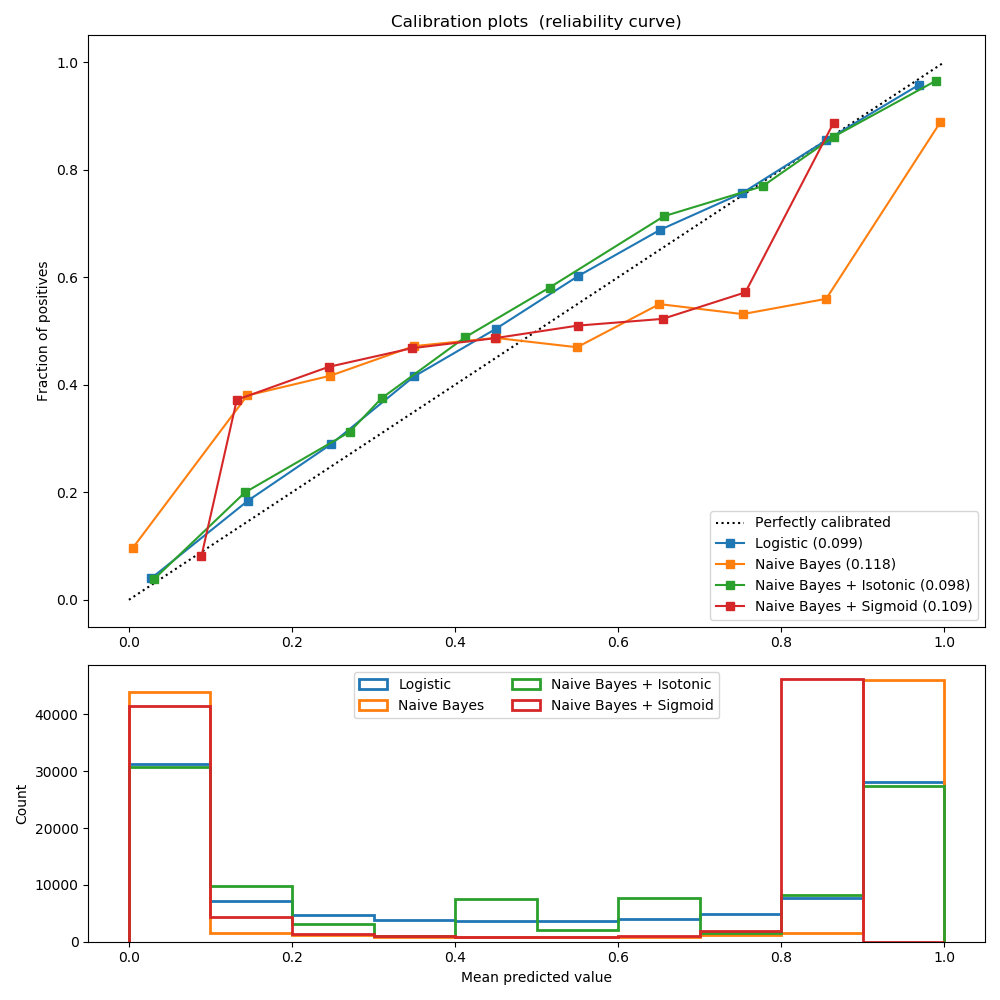
Brier分數越小越好,因此命名為“loss”。在一組N個預測中的所有項目上,Brier分數測量(1)分配給項目i可能結果的預測概率與(2)實際結果之間的均方差。因此,一組預測的Brier分數越低,則對預測的校準就越好。請注意,Brier分數始終取0到1之間的值,因為這是預測概率(必須在0到1之間)和實際結果(只能取0到1)之間的最大可能差值。)。Brier loss由精制損失和校準損失組成。 Brier得分適用于可以構造為真或假的二進制和分類結果,但不適用于可以采用三個或更多值的序數變量(這是因為Brier分數假設所有可能的結果的彼此“距離”相等)。哪個標簽被視為肯定標簽是通過參數pos_label(默認值為1)控制的。請閱讀用戶指南中的更多內容。
| 參數 | 說明 |
|---|---|
| y_true | array, shape (n_samples,) 實際targets。 |
| y_prob | array, shape (n_samples,) 正類的概率。 |
| sample_weight | array-like of shape (n_samples,), default=None 樣本權重。 |
| pos_label | int or str, default=None 正向類別的標簽。除非y_true為全0或全為-1時pos_label默認為1;否則默認為更大的標簽。 |
| 返回值 | 說明 |
|---|---|
| score | float Brier得分。 |
參考
1 Wikipedia entry for the Brier score.
示例
>>> import numpy as np
>>> from sklearn.metrics import brier_score_loss
>>> y_true = np.array([0, 1, 1, 0])
>>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
>>> y_prob = np.array([0.1, 0.9, 0.8, 0.3])
>>> brier_score_loss(y_true, y_prob)
0.037...
>>> brier_score_loss(y_true, 1-y_prob, pos_label=0)
0.037...
>>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham")
0.037...
>>> brier_score_loss(y_true, np.array(y_prob) > 0.5)
0.0