科學數據處理統計學習指南?
統計學習
機器學習是一項越來越重要的技術,因為實驗科學面臨的數據集規模正在迅速增長。 它所解決的問題包括建立鏈接不同觀察值的預測功能,對觀察值進行分類或學習未標記數據集中的結構。
本教程將探討統計學習,以及將機器學習技術用于統計推斷的目的:在手頭的數據上得出結論。
Scikit-learn是一個Python模塊,在緊密結合的科學Python程序包世界(NumPy,SciPy,matplotlib)中集成了經典的機器學習算法。
統計學習:scikit-learn中的設置和估計對象
數據集
Scikit-learn處理來自一個或多個以2D數組表示的數據集的學習信息。它們可以理解為多維觀測的列表。我們說這些數組的第一個軸是樣本軸,而第二個是特征軸。
scikit-learn附帶的一個簡單示例:iris數據集:
from sklearn import datasets
iris = datasets.load_iris()
data = iris.data
data.shape
輸出:
(150,4)
它由150個鳶尾花的觀察數據組成,每個觀察都由4個特征描述:它們的萼片和花瓣的長度和寬度,詳細信息請參見iris.DESCR。
當數據最初不是(n_samples,n_features)形狀時,需要對其進行預處理,以供scikit-learn使用。
重塑數據的一個例子是數字數據集:
數字數據集由1797個8x8手寫數字圖像組成,如圖所示:

digits = datasets.load_digits()
digits.images.shape
import matplotlib.pyplot as plt
plt.imshow(digits.images[-1], cmap=plt.cm.gray_r)
輸出:
(1797, 8, 8)
<matplotlib.image.AxesImage object at ...>
為了將此數據集與scikit-learn一起使用,我們將每個8x8圖像轉換為長度為64的特征向量:
data = digits.images.reshape((digits.images.shape[0], -1))
估計對象
擬合數據:scikit-learn實現的主要API是估算器。估計器是從數據中學習的任何對象。它可以是分類,回歸或聚類算法,也可以是從原始數據中提取/過濾有用特征的轉換器。
所有估算器對象都公開一個帶數據集(通常為二維數組)的fit方法:
estimator.fit(data)
估算器參數:可以在實例化估計器或通過修改相應屬性來設置估計器的所有參數:
estimator = Estimator(param1 = 1,param2 = 2)
estimator.param1
輸出:
1
估計出的參數:當數據裝有估計器時,參數是根據現有數據估計的。所有估計的參數都是估計對象的屬性,其下劃線結尾:
estimator.estimated_param_
有監督的學習:從高維觀測值預測輸出變量
監督學習中解決的問題
監督學習包括學習兩個數據集之間的鏈接:觀測數據X和我們試圖預測的外部變量y,通常稱為“目標”或“標簽”。 y通常是長度為n_samples的一維數組。
scikit-learn中所有受監督的估計器都執行fit(X,y)方法以擬合模型,并執行predict(X)方法,給定未標記的觀察值X,該方法返回預測的標記y。
詞匯:分類和回歸
如果預測任務是將觀察結果分類為一組有限標簽,換句話說就是“命名”觀察到的對象,則該任務稱為分類任務。另一方面,如果目標是預測連續目標變量,則稱其為回歸任務。
在scikit-learn中進行分類時,y是整數或字符串的向量。
注意:有關scikit-learn中使用的基本機器學習詞匯的快速指南,請參見scikit-learn機器學習簡介教程。
最近鄰和維度詛咒
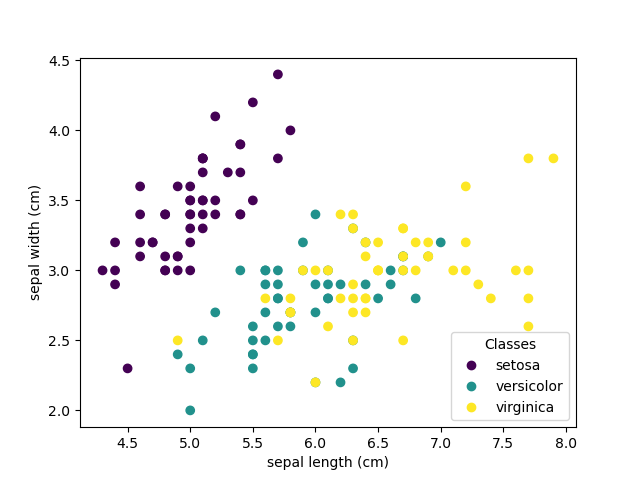
分類鳶尾花數據集: 鳶尾花數據集是一項分類任務,包括從其花瓣和萼片的長度和寬度中識別出3種不同類型的鳶尾花(Setosa,Versicolour和Virginica):
import numpy as np
from sklearn import datasets
iris_X, iris_y = datasets.load_iris(return_X_y=True)
np.unique(iris_y)
輸出:
array([0, 1, 2])
k近鄰分類器
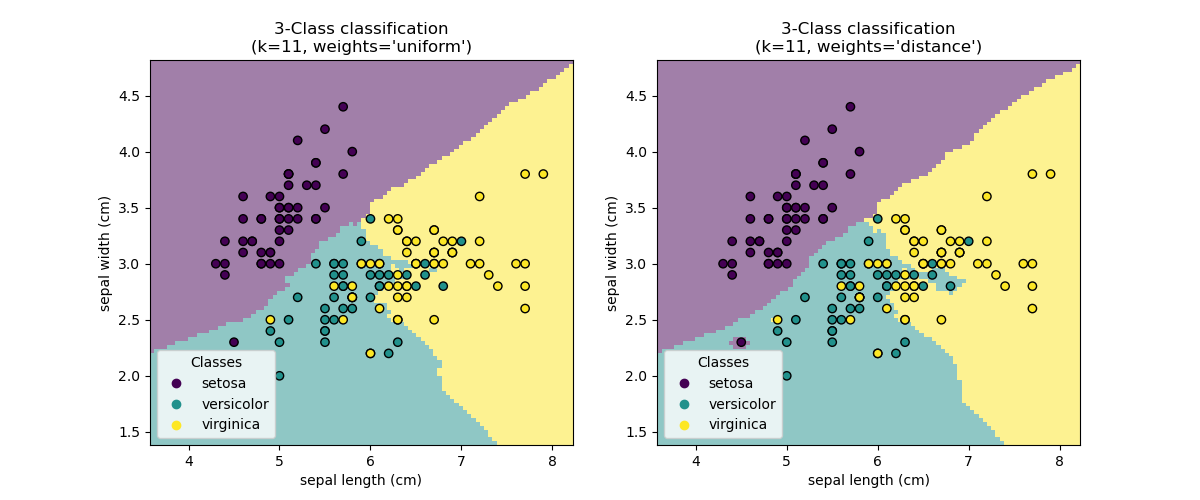
最簡單的分類器是最近鄰分類器:給定新的觀測值X_test,在訓練集中(即用于訓練估計器的數據)找到具有最近特征向量的觀測值。(有關這種類型的分類器的更多信息,請參見在線Scikit-learn文檔的Nearest Neighbors部分。)
訓練集和測試集
在嘗試使用任何學習算法進行實驗時,重要的是不要在用于擬合估算器的數據上測試估算器的預測,因為這不會評估新數據上估算器的性能。 這就是為什么數據集經常被分成訓練和測試數據的原因。
KNN(k個最近鄰)分類示例:
# 在訓練和測試數據中分割鳶尾花數據
# 隨機排列,隨機分割數據
np.random.seed(0)
indices = np.random.permutation(len(iris_X))
iris_X_train = iris_X[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
iris_X_test = iris_X[indices[-10:]]
iris_y_test = iris_y[indices[-10:]]
# 創建并擬合最近鄰分類器
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()
knn.fit(iris_X_train, iris_y_train)
knn.predict(iris_X_test)
iris_y_test
輸出:
KNeighborsClassifier()
array([1, 2, 1, 0, 0, 0, 2, 1, 2, 0])
array([1, 1, 1, 0, 0, 0, 2, 1, 2, 0])
維度詛咒
為了使估算器有效,您需要相鄰點之間的距離小于某個值,這取決于問題。在一個維度上,這平均需要 點。在上述 -NN 示例的上下文中,如果僅通過一個值在0到1范圍內的特征和訓練觀察來描述數據,則新數據將比距離遠出。因此,與類間特征變化的規模相比,最近的鄰居決策規則將很快變得有效。
如果要素數量為,則現在需要 個點。假設我們在一個維度上需要10個點:現在,在維度的空間上則需要個點才能鋪平[0,1]空間。隨著變得越來越大,一個好的估計量所需的訓練點數呈指數增長。
例如,如果每個點僅是一個數字(8個字節),那么在大約的維度上有效的-NN估計量將需要比整個互聯網的當前估計大小(±1000艾字節左右)更多的訓練數據。
這稱為維數詛咒,是機器學習解決的核心問題。
線性模型:從回歸到稀疏
糖尿病數據集
糖尿病數據集包含442位患者的10個生理變量(年齡,性別,體重,血壓),并顯示一年后疾病進展的指標:
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]
當前的任務是根據生理變量預測疾病的進展。
線性回歸
LinearRegression最簡單的形式是通過調整一組參數將線性模型擬合到數據集,以使模型的殘差平方和盡可能小。
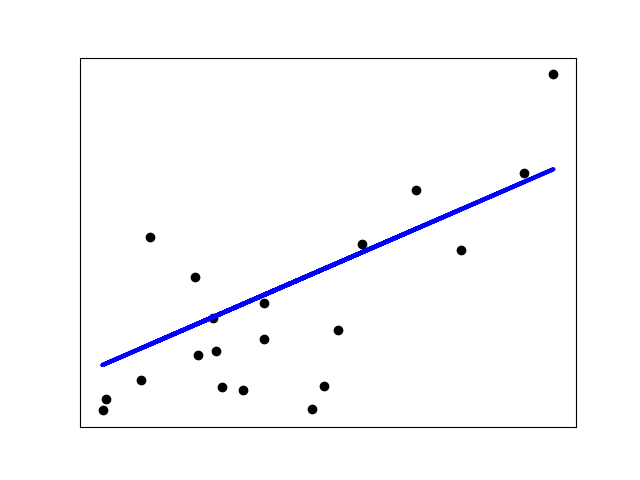
線性模型:
:數據
:目標變量
:系數
:觀察噪聲
from sklearn import linear_model
regr = linear_model.LinearRegression()
regr.fit(diabetes_X_train, diabetes_y_train)
print(regr.coef_)
# 均方誤差
np.mean((regr.predict(diabetes_X_test) - diabetes_y_test)**2)
# 解釋方差得分:1是完美預測,0表示X和y之間沒有線性關系。
regr.score(diabetes_X_test, diabetes_y_test)
輸出:
[ 0.30349955 -237.63931533 510.53060544 327.73698041 -814.13170937
492.81458798 102.84845219 184.60648906 743.51961675 76.09517222]
2004.56760268...
0.5850753022690...
緊縮
如果每個維度的數據點很少,則觀測值中的噪聲會引起高方差:
X = np.c_[ .5, 1].T
y = [.5, 1]
test = np.c_[ 0, 2].T
regr = linear_model.LinearRegression()
import matplotlib.pyplot as plt
plt.figure()
np.random.seed(0)
for _ in range(6):
this_X = .1 * np.random.normal(size=(2, 1)) + X
regr.fit(this_X, y)
plt.plot(test, regr.predict(test))
plt.scatter(this_X, y, s=3)
高維統計學習的一種解決方案是將回歸系數縮小為零:任意兩個隨機選擇的觀察值很可能是不相關的。 這稱為Ridge回歸:
regr = linear_model.Ridge(alpha=.1)
plt.figure()
np.random.seed(0)
for _ in range(6):
this_X = .1 * np.random.normal(size=(2, 1)) + X
regr.fit(this_X, y)
plt.plot(test, regr.predict(test))
plt.scatter(this_X, y, s=3)
這是偏差/方差折衷的一個示例:脊alpha參數越大,偏差越大,方差越小。
我們可以選擇α以最大程度地減少遺漏的錯誤,這次使用糖尿病數據集而不是我們的綜合數據:
alphas = np.logspace(-4, -1, 6)
print([regr.set_params(alpha=alpha)
.fit(diabetes_X_train, diabetes_y_train)
.score(diabetes_X_test, diabetes_y_test)
for alpha in alphas])
輸出:
[0.5851110683883..., 0.5852073015444..., 0.5854677540698...,
0.5855512036503..., 0.5830717085554..., 0.57058999437...]
注意:捕獲阻止模型泛化為新數據的擬合參數噪聲稱為過擬合。 脊回歸帶來的偏差稱為正則化。
稀疏性
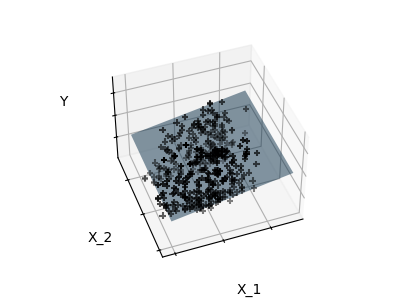
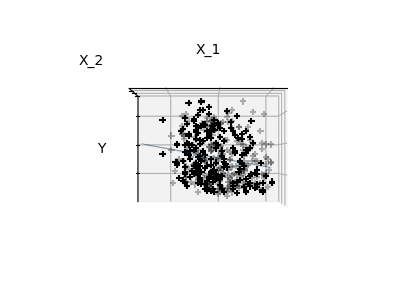
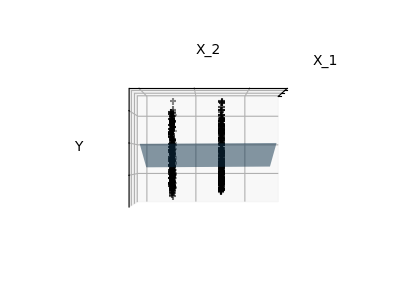
注意:完整的糖尿病數據集的表示將涉及11個維度(10個特征維度和一個目標變量)。 很難就這種表示法建立一種直覺,但記住這將是一個相當空的空間,這可能會很有用。
我們可以看到,盡管特征2在整個模型中具有很強的系數,但是當與特征1一起考慮時,它傳達的y信息很少。
為了改善問題的狀況(即減輕維度詛咒),僅選擇信息性特征并將非信息性特征(例如特征2設置為0)會很有趣。Ridge回歸會減少其貢獻,但不會設置 他們為零。 另一種懲罰方法稱為Lasso(最小絕對收縮和選擇算子),可以將一些系數設置為零。 這種方法稱為稀疏方法,稀疏性可以看作是Occam剃刀的一種應用:更喜歡簡單的模型。
regr = linear_model.Lasso()
scores = [regr.set_params(alpha=alpha)
.fit(diabetes_X_train, diabetes_y_train)
.score(diabetes_X_test, diabetes_y_test)
for alpha in alphas]
best_alpha = alphas[scores.index(max(scores))]
regr.alpha = best_alpha
regr.fit(diabetes_X_train, diabetes_y_train)
print(regr.coef_)
輸出:
Lasso(alpha=0.025118864315095794)
[ 0. -212.43764548 517.19478111 313.77959962 -160.8303982 -0.
-187.19554705 69.38229038 508.66011217 71.84239008]
針對同一問題的不同算法
可以使用不同的算法來解決相同的數學問題。 例如,scikit-learn中的套索對象使用坐標下降法解決了套索回歸問題,該方法在大型數據集上非常有效。 但是,scikit-learn還使用LARS算法提供了LassoLars對象,對于估計的權重向量非常稀疏的問題(即觀察很少的問題)非常有效。
分類
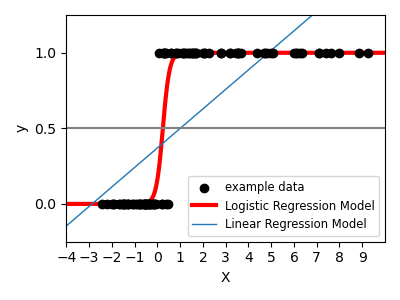
對于分類,如在標記虹膜任務中一樣,線性回歸不是正確的方法,因為它將對遠離決策邊界的數據賦予過多的權重。 線性方法是擬合S型函數或邏輯函數:
輸入:
log = linear_model.LogisticRegression(C=1e5)
log.fit(iris_X_train, iris_y_train)
輸出:
LogisticRegression(C=100000.0)
這就是知名的邏輯回歸:
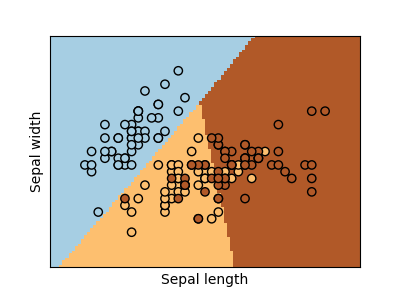
多標簽分類
如果您要預測多個類別,則經常使用的選擇是對所有分類器進行擬合,然后使用投票啟發法進行最終決策。
邏輯回歸的收縮率和稀疏性
C參數控制LogisticRegression對象中的正則化量:C的值較大會導致正則化程度降低。 懲罰=“ l2”給出收縮率(即非稀疏系數),而懲罰=“ l1”給出稀疏性。
練習
嘗試用最近的鄰居和線性模型對數字數據集進行分類。 忽略最后的10%,并根據這些觀察結果測試預測性能。
from sklearn import datasets, neighbors, linear_model
X_digits, y_digits = datasets.load_digits(return_X_y=True)
X_digits = X_digits / X_digits.max()
解決方案:https://scikit-learn.org/stable/_downloads/bfcebce45024b267e8546d6914acfedc/plot_digits_classification_exercise.py
支持向量機(SVM)
線性支持向量機
支持向量機屬于判別模型家族:它們試圖找到樣本的組合以構建一個平面,以最大化兩個類別之間的余量。 正則化是由C參數設置的:C的值較小意味著使用分隔線附近的許多或所有觀測值來計算裕度(更正則化); C的值較大,表示在接近分隔線的觀察值上計算裕度(較少的正則化)。
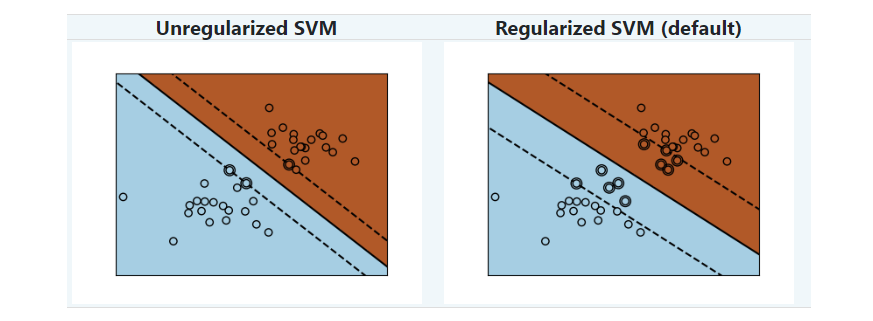
示例:
SVM可用于回歸–SVR(支持向量回歸)–或分類–SVC(支持向量分類)。
from sklearn import svm
svc = svm.SVC(kernel='linear')
svc.fit(iris_X_train, iris_y_train)
輸出:
SVC(kernel='linear')
警告:歸一化數據
對于包括SVM在內的許多估算器而言,對于每個要素而言,擁有具有單位標準差的數據集對于獲得良好的預測至關重要。
使用核函數
在要素空間中,類并非總是線性可分離的。 解決方案是建立一個決策函數,該決策函數不是線性的,而是可以是多項式的。 這是使用內核技巧完成的,該技巧可以看作是通過將內核置于觀察值上來創建決策能量:

互動范例
參見SVM GUI以下載svm_gui.py;。 使用左右按鈕添加兩個類別的數據點,擬合模型并更改參數和數據。
練習
嘗試使用SVM對虹膜數據集中的第1類和第2類進行分類,并具有2個主要特征。 忽略每堂課的10%,并根據這些觀察結果測試預測性能。
警告:課程是有序的,請不要遺漏最后的10%,您只能在一個課程上進行測試。
提示:您可以在網格上使用Decision_function方法來獲取一些感覺。

輸入:
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y != 0, :2]
y = y[y != 0]
解決方案見:https://scikit-learn.org/stable/_downloads/91f0cd01beb5b964a5e1ece5bdd15499/plot_iris_exercise.py
模型選擇:選擇估計量及其參數
分數和交叉驗證的分數
如我們所見,每個估算器都公開一種計分方法,該方法可以判斷新數據的擬合(或預測)質量。 越大越好。
from sklearn import datasets, svm
X_digits, y_digits = datasets.load_digits(return_X_y=True)
svc = svm.SVC(C=1, kernel='linear')
svc.fit(X_digits[:-100], y_digits[:-100]).score(X_digits[-100:], y_digits[-100:])
輸出:
0.98
為了更好地衡量預測準確性(我們可以將其用作模型擬合優度的代理),我們可以將數據依次分成折疊,用于訓練和測試:
import numpy as np
X_folds = np.array_split(X_digits, 3)
y_folds = np.array_split(y_digits, 3)
scores = list()
for k in range(3):
# We use 'list' to copy, in order to 'pop' later on
X_train = list(X_folds)
X_test = X_train.pop(k)
X_train = np.concatenate(X_train)
y_train = list(y_folds)
y_test = y_train.pop(k)
y_train = np.concatenate(y_train)
scores.append(svc.fit(X_train, y_train).score(X_test, y_test))
print(scores)
輸出:
[0.934..., 0.956..., 0.939...]
這被叫做K折交叉驗證。
交叉驗證生成器
Scikit-learn具有一組類,這些類可用于生成流行的交叉驗證策略的訓練/測試索引列表。
他們公開了一個拆分方法,該方法接受要拆分的輸入數據集,并為所選交叉驗證策略的每次迭代生成訓練/測試集索引。
本示例顯示了split方法的示例用法。
輸入:
from sklearn.model_selection import KFold, cross_val_score
X = ["a", "a", "a", "b", "b", "c", "c", "c", "c", "c"]
k_fold = KFold(n_splits=5)
for train_indices, test_indices in k_fold.split(X):
print('Train: %s | test: %s' % (train_indices, test_indices))
輸出:
Train: [2 3 4 5 6 7 8 9] | test: [0 1]
Train: [0 1 4 5 6 7 8 9] | test: [2 3]
Train: [0 1 2 3 6 7 8 9] | test: [4 5]
Train: [0 1 2 3 4 5 8 9] | test: [6 7]
Train: [0 1 2 3 4 5 6 7] | test: [8 9]
然后可以輕松執行交叉驗證:
[svc.fit(X_digits[train], y_digits[train]).score(X_digits[test], y_digits[test]) for train, test in k_fold.split(X_digits)]
輸出:
[0.963..., 0.922..., 0.963..., 0.963..., 0.930...]
可以使用cross_val_score幫助器直接計算交叉驗證得分。 給定一個估算器,交叉驗證對象和輸入數據集,cross_val_score將數據重復拆分為一個訓練和一個測試集,使用該訓練集訓練該估算器,并根據測試集計算交叉算子的每次迭代的得分 驗證。
默認情況下,估算器的得分方法用于計算各個得分。
請參閱指標模塊以了解有關可用評分方法的更多信息。
cross_val_score(svc, X_digits, y_digits, cv=k_fold, n_jobs=-1)
輸出:
array([0.96388889, 0.92222222, 0.9637883 , 0.9637883 , 0.93036212])
n_jobs = -1表示將在計算機的所有CPU上調度計算。
可替代地,可以提供計分參數以指定替代的計分方法。
cross_val_score(svc, X_digits, y_digits, cv=k_fold,
scoring='precision_macro')
輸出:
array([0.96578289, 0.92708922, 0.96681476, 0.96362897, 0.93192644])
交叉驗證生成器
KFold (n_splits, shuffle, random_state) |
StratifiedKFold (n_splits, shuffle, random_state) |
GroupKFold (n_splits) |
|---|---|---|
| 將其拆分為K折,在K-1上訓練,然后在左側進行測試。 | 與K折相同,但保留每個折內的類分布。 | 確保同一組不在測試和培訓集中 |
ShuffleSplit (n_splits, test_size, train_size, random_state) |
StratifiedShuffleSplit |
GroupShuffleSplit |
| 根據隨機排列生成訓練/測試索引。 | 與shuffle split相同,但保留每次迭代內的類分布。 | 確保同一組不在測試和培訓集中。 |
LeaveOneGroupOut () |
LeavePGroupsOut (n_groups) |
LeaveOneOut () |
| 采用組數組對觀察進行分組。 | 忽略P組 | 忽略指定的一個觀察值。 |
LeavePOut (p) |
PredefinedSplit |
|
| 忽略P個觀察值 | 根據預定義的拆分生成訓練/測試索引。 |
練習
在數字數據集上,繪制具有線性核的SVC估計量的交叉驗證得分作為參數C的函數(使用點的對數網格,范圍為1到10)。

import numpy as np
from sklearn.model_selection import cross_val_score
from sklearn import datasets, svm
X, y = datasets.load_digits(return_X_y=True)
svc = svm.SVC(kernel='linear')
C_s = np.logspace(-10, 0, 10)
scores = list()
解決方案見鏈接:手寫數據集上的交叉驗證
網格搜索和交叉驗證的估計量
網格搜索
scikit-learn提供了一個對象,該對象在給定數據的情況下,在參數網格上的估計器擬合期間計算分數,并選擇參數以最大化交叉驗證分數。 該對象在構造期間接受一個估算器,并公開一個估算器API:
from sklearn.model_selection import GridSearchCV, cross_val_score
Cs = np.logspace(-6, -1, 10)
clf = GridSearchCV(estimator=svc, param_grid=dict(C=Cs),
n_jobs=-1)
clf.fit(X_digits[:1000], y_digits[:1000])
clf.best_score_
clf.best_estimator_.C
# 測試集的預測性能不如訓練集
clf.score(X_digits[1000:], y_digits[1000:])
輸出:
GridSearchCV(cv=None,...)
0.925...
0.0077...
0.943...
默認情況下,GridSearchCV使用3倍交叉驗證。但是,如果檢測到通過了分類器而不是回歸器,則使用分層的3倍。默認值將在版本0.22中更改為5倍交叉驗證。
嵌套交叉驗證
cross_val_score(clf, X_digits, y_digits)
輸出:
array([0.938..., 0.963..., 0.944...])
并行執行兩個交叉驗證循環:一個由GridSearchCV估計器設置gamma,另一個由cross_val_score來測量估計器的預測性能。所得分數是對新數據的預測分數的無偏估計。
警告:不能嵌套使用并行計算的對象(n_jobs不同于1)。
交叉驗證的估計量
可以在逐個算法的基礎上更高效地完成交叉驗證以設置參數。這就是為什么對于某些估計器,scikit-learn會顯示交叉驗證:評估通過交叉驗證自動設置其參數的估計器性能估計器:
from sklearn import linear_model, datasets
lasso = linear_model.LassoCV()
X_diabetes, y_diabetes = datasets.load_diabetes(return_X_y=True)
lasso.fit(X_diabetes, y_diabetes)
# 估算器自動選擇其lambda:
lasso.alpha_
輸出:
LassoCV()
0.00375...
這些估算器的名稱與對應估算器的名稱類似,后綴“ CV”。
練習
在糖尿病數據集上,找到最佳正則化參數alpha。
獎勵:您對選擇出的alpha有多少信心?
from sklearn import datasets
from sklearn.linear_model import LassoCV
from sklearn.linear_model import Lasso
from sklearn.model_selection import KFold
from sklearn.model_selection import GridSearchCV
X, y = datasets.load_diabetes(return_X_y=True)
X = X[:150]
解決方案:糖尿病數據集上的交叉驗證練習
無監督學習:尋求數據表示
聚類:將觀察分組在一起
聚類中解決的問題:
在給定鳶尾花數據集的情況下,如果我們知道虹膜有3種類型,但沒有分類學家來標記它們的話:我們可以嘗試進行聚類任務:將觀察結果分成分離良好的一組,稱為聚類。
K均值聚類
請注意,存在許多不同的聚類標準和相關算法。 最簡單的聚類算法是K-means。

輸入:
from sklearn import cluster, datasets
X_iris, y_iris = datasets.load_iris(return_X_y=True)
k_means = cluster.KMeans(n_clusters=3)
k_means.fit(X_iris)
print(k_means.labels_[::10])
print(y_iris[::10])
輸出:
KMeans(n_clusters=3)
[1 1 1 1 1 0 0 0 0 0 2 2 2 2 2]
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]
警告:聚類絕對不能保證恢復基本事實(譯者注:即找到真實標簽)。 首先,很難選擇正確數量的群集。 其次,盡管scikit-learn使用了幾種技巧來緩解此問題,但是該算法對初始化很敏感,并且可以陷入局部最小值。

不要過度解讀聚類結果。
應用示例:矢量量化
一般而言,尤其是KMeans,聚類可以看作是選擇少量樣本來壓縮信息的一種方式。 該問題有時稱為矢量量化。 例如,這可以用于后繼圖像:
import scipy as sp
try:
face = sp.face(gray=True)
except AttributeError:
from scipy import misc
face = misc.face(gray=True)
X = face.reshape((-1, 1)) # We need an (n_sample, n_feature) array
k_means = cluster.KMeans(n_clusters=5, n_init=1)
k_means.fit(X)
values = k_means.cluster_centers_.squeeze()
labels = k_means.labels_
face_compressed = np.choose(labels, values)
face_compressed.shape = face.shape
輸出:
KMeans(n_clusters=5, n_init=1)

分層聚集聚類:Ward
層次聚類方法是一種聚類分析,旨在建立聚類的層次。通常,此技術的各種方法是:
集聚-自下而上的方法:每個觀察都從其自己的簇開始,并且以最小化鏈接標準的方式迭代地合并簇。當感興趣的簇僅由少量觀察組成時,這種方法特別有趣。當簇數很大時,它的計算效率比k均值高得多。
分裂-自上而下的方法:所有觀察都始于一個簇,當一個簇向下移動時,它將被迭代地拆分。對于估計大量聚類,此方法既緩慢(由于所有觀察都是從一個聚類開始,然后遞歸拆分),而且在統計上是不適定的。
連接受限的集群
通過聚集聚類,可以通過提供連通性圖來指定可以將哪些樣本聚在一起。 scikit-learn中的圖由它們的鄰接矩陣表示。通常,使用稀疏矩陣。例如,在對圖像進行聚類時,這對于檢索連接的區域(有時也稱為連接的組件)很有用。

from skimage.data import coins
from scipy.ndimage.filters import gaussian_filter
from skimage.transform import rescale
rescaled_coins = rescale(
gaussian_filter(coins(), sigma=2),
0.2, mode='reflect', anti_aliasing=False, multichannel=False
)
X = np.reshape(rescaled_coins, (-1, 1))
我們需要圖像的矢量化版本。 'rescaled_coins'是硬幣圖像的縮小版本,以加快處理速度:
from sklearn.feature_extraction import grid_to_graph
connectivity = grid_to_graph(*rescaled_coins.shape)
定義數據的圖形結構。連接到鄰近的像素:
n_clusters = 27 #簇的數量
from sklearn.cluster import AgglomerativeClustering
ward = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward',
connectivity=connectivity)
ward.fit(X)
label = np.reshape(ward.labels_, rescaled_coins.shape)
輸出:
AgglomerativeClustering(connectivity=..., n_clusters=27)
功能集聚
我們已經看到稀疏性可以用來減輕維數的詛咒,即與特征數量相比,觀測值不足。另一種方法是將相似的特征融合在一起:特征集聚。可以通過在特征方向上進行聚類(換句話說,對轉置后的數據進行聚類)來實現此方法。
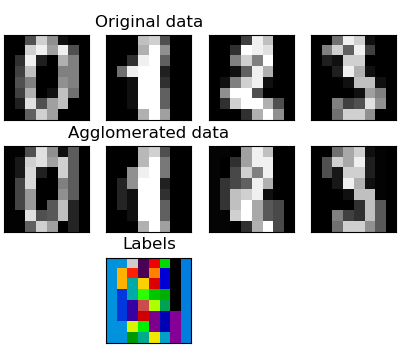
digits = datasets.load_digits()
images = digits.images
X = np.reshape(images, (len(images), -1))
connectivity = grid_to_graph(*images[0].shape)
agglo = cluster.FeatureAgglomeration(connectivity=connectivity,
n_clusters=32)
agglo.fit(X)
X_reduced = agglo.transform(X)
X_approx = agglo.inverse_transform(X_reduced)
images_approx = np.reshape(X_approx, images.shape)
輸出:
FeatureAgglomeration(connectivity=..., n_clusters=32)
轉換和逆轉換(inverse_transform)方法
一些估計器會公開一種轉換方法,例如以減少數據集的維數。
分解:從信號到分量和負載
組件(成分/特征)和負載
如果X是我們的多元數據,那么我們要解決的問題是在不同的觀察基礎上重寫它:我們想學習載荷L和一組分量C,使得X = LC。存在選擇的不同標準組件
主成分分析:PCA
主成分分析(PCA)選擇解釋信號中最大方差的連續成分。


上面觀察到的點云在一個方向上非常平坦:三個單變量特征之一幾乎可以使用另外兩個來精確計算。 PCA尋找數據不一致的方向。
當用于轉換數據時,PCA可以通過投影在主要子空間上來降低數據的維數。
#創建一個僅2個有用維度的信號
x1 = np.random.normal(size=100)
x2 = np.random.normal(size=100)
x3 = x1 + x2
X = np.c_[x1, x2, x3]
from sklearn import decomposition
pca = decomposition.PCA()
pca.fit(X)
print(pca.explained_variance_)
輸出:
[ 2.18565811e+00 1.19346747e+00 8.43026679e-32]
如我們所見,只有前兩個組件是有用的。
pca.n_components = 2
X_reduced = pca.fit_transform(X)
X_reduced.shape
輸出:
(100, 2)
獨立成分分析:ICA
獨立組件分析(ICA)選擇組件,以便它們的載荷分布具有最大數量的獨立信息。 它能夠恢復非高斯獨立信號:
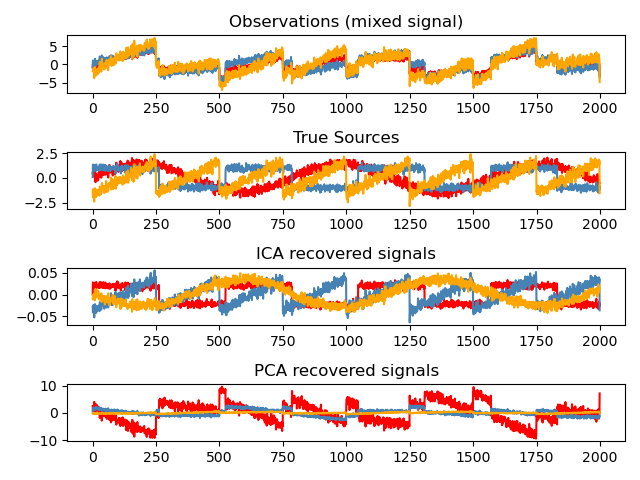
# 獲取樣本數據
import numpy as np
from scipy import signal
time = np.linspace(0, 10, 2000)
s1 = np.sin(2 * time) # 信號1 : 正弦信號
s2 = np.sign(np.sin(3 * time)) # 信號2:方波信號
s3 = signal.sawtooth(2 * np.pi * time) # 信號3: 鋸齒信號
S = np.c_[s1, s2, s3]
S += 0.2 * np.random.normal(size=S.shape) # 增加噪音
S /= S.std(axis=0) # 標準化數據
# 混合數據
A = np.array([[1, 1, 1], [0.5, 2, 1], [1.5, 1, 2]]) # 混和矩陣
X = np.dot(S, A.T) # 獲取觀測值
# 計算ICA
ica = decomposition.FastICA()
S_ = ica.fit_transform(X) # 得到預測結果
A_ = ica.mixing_.T
np.allclose(X, np.dot(S_, A_) + ica.mean_)
輸出:
True
全部放在一起
管道
我們已經看到,一些估計器可以轉換數據,并且一些估計器可以預測變量。 我們還可以創建組合的估計量:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
# 定義管道以搜索PCA截斷和分類器正則化的最佳組合。
pca = PCA()
# 將公差設置為較大的值可以使示例更快
logistic = LogisticRegression(max_iter=10000, tol=0.1)
pipe = Pipeline(steps=[('pca', pca), ('logistic', logistic)])
X_digits, y_digits = datasets.load_digits(return_X_y=True)
# 可以使用__分隔的參數名稱來設置管道的參數:
param_grid = {
'pca__n_components': [5, 15, 30, 45, 64],
'logistic__C': np.logspace(-4, 4, 4),
}
search = GridSearchCV(pipe, param_grid, n_jobs=-1)
search.fit(X_digits, y_digits)
print("Best parameter (CV score=%0.3f):" % search.best_score_)
print(search.best_params_)
# 繪制PCA色譜
pca.fit(X_digits)
fig, (ax0, ax1) = plt.subplots(nrows=2, sharex=True, figsize=(6, 6))
ax0.plot(np.arange(1, pca.n_components_ + 1),
pca.explained_variance_ratio_, '+', linewidth=2)
ax0.set_ylabel('PCA explained variance ratio')
ax0.axvline(search.best_estimator_.named_steps['pca'].n_components,
linestyle=':', label='n_components chosen')
ax0.legend(prop=dict(size=12))
特征臉的人臉識別
本示例中使用的數據集是“未經處理的、有標簽的人臉”(也稱為LFW)的預處理摘錄:
http://vis-www.cs.umass.edu/lfw/lfw-funneled.tgz(233MB)
"""
===================================================
使用特征臉和SVM的臉部識別示例
===================================================
本示例中使用的數據集是“貼有標簽的未經處理的面孔”,又名LFW_:
http://vis-www.cs.umass.edu/lfw/lfw-funneled.tgz(233MB)
.._ LFW:http://vis-www.cs.umass.edu/lfw/
數據集中排名前5名的人員的預期結果:
================================================== =
================== ============ ======= ========== =======
precision recall f1-score support
================== ============ ======= ========== =======
Ariel Sharon 0.67 0.92 0.77 13
Colin Powell 0.75 0.78 0.76 60
Donald Rumsfeld 0.78 0.67 0.72 27
George W Bush 0.86 0.86 0.86 146
Gerhard Schroeder 0.76 0.76 0.76 25
Hugo Chavez 0.67 0.67 0.67 15
Tony Blair 0.81 0.69 0.75 36
avg / total 0.80 0.80 0.80 322
================== ============ ======= ========== =======
"""
from time import time
import logging
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import fetch_lfw_people
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
from sklearn.svm import SVC
print(__doc__)
# 在標準輸出上顯示進度日志
logging.basicConfig(level=logging.INFO, format='%(asctime)s %(message)s')
# #############################################################################
# 下載數據(如果尚未存儲在磁盤上)并將其作為numpy數組加載
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
# 內省圖像數組以找到形狀(用于繪制)
n_samples, h, w = lfw_people.images.shape
# 對于機器學習,我們直接使用這2個數據(因為相對像素位置信息被該模型忽略)
X = lfw_people.data
n_features = X.shape[1]
# 要預測的標簽是該人的身份證
y = lfw_people.target
target_names = lfw_people.target_names
n_classes = target_names.shape[0]
print("Total dataset size:")
print("n_samples: %d" % n_samples)
print("n_features: %d" % n_features)
print("n_classes: %d" % n_classes)
# #############################################################################
# 使用分層k折分為訓練集和測試集
# 分割需練級與測試集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.25, random_state=42)
# #############################################################################
# 在人臉數據集(視為未標記數據集)上計算PCA(特征臉):無監督特征提取/降維
n_components = 150
print("Extracting the top %d eigenfaces from %d faces"
% (n_components, X_train.shape[0]))
t0 = time()
pca = PCA(n_components=n_components, svd_solver='randomized',
whiten=True).fit(X_train)
print("done in %0.3fs" % (time() - t0))
eigenfaces = pca.components_.reshape((n_components, h, w))
print("Projecting the input data on the eigenfaces orthonormal basis")
t0 = time()
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("done in %0.3fs" % (time() - t0))
# #############################################################################
# 訓練SVM分類模型
print("Fitting the classifier to the training set")
t0 = time()
param_grid = {'C': [1e3, 5e3, 1e4, 5e4, 1e5],
'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1], }
clf = GridSearchCV(
SVC(kernel='rbf', class_weight='balanced'), param_grid
)
clf = clf.fit(X_train_pca, y_train)
print("done in %0.3fs" % (time() - t0))
print("Best estimator found by grid search:")
print(clf.best_estimator_)
# #############################################################################
# 對測試集中的模型質量進行定量評估
print("Predicting people's names on the test set")
t0 = time()
y_pred = clf.predict(X_test_pca)
print("done in %0.3fs" % (time() - t0))
print(classification_report(y_test, y_pred, target_names=target_names))
print(confusion_matrix(y_test, y_pred, labels=range(n_classes)))
# #############################################################################
# 使用matplotlib對預測進行定性評估
def plot_gallery(images, titles, h, w, n_row=3, n_col=4):
"""Helper function to plot a gallery of portraits"""
plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
for i in range(n_row * n_col):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
plt.title(titles[i], size=12)
plt.xticks(())
plt.yticks(())
# 在測試集的一部分上繪制預測結果
def title(y_pred, y_test, target_names, i):
pred_name = target_names[y_pred[i]].rsplit(' ', 1)[-1]
true_name = target_names[y_test[i]].rsplit(' ', 1)[-1]
return 'predicted: %s\ntrue: %s' % (pred_name, true_name)
prediction_titles = [title(y_pred, y_test, target_names, i)
for i in range(y_pred.shape[0])]
plot_gallery(X_test, prediction_titles, h, w)
# 繪制最有意義的特征臉圖庫
eigenface_titles = ["eigenface %d" % i for i in range(eigenfaces.shape[0])]
plot_gallery(eigenfaces, eigenface_titles, h, w)
plt.show()
輸出:

數據集中排名前5名的人員的預期結果:
precision recall f1-score support
Gerhard_Schroeder 0.91 0.75 0.82 28
Donald_Rumsfeld 0.84 0.82 0.83 33
Tony_Blair 0.65 0.82 0.73 34
Colin_Powell 0.78 0.88 0.83 58
George_W_Bush 0.93 0.86 0.90 129
avg / total 0.86 0.84 0.85 282
未解決的問題:股票市場結構
我們可以預測給定時間內Google的股價變化嗎?
尋求幫助
項目郵件清單
如果您遇到scikit-learn的錯誤,或者需要在文檔字符串或在線文檔中進行說明,請隨時在郵件列表中詢問。
機器學習從業者問答社區
| 網站 | 說明 |
|---|---|
| Quora.com | Quora有一個與機器學習相關的問題的主題,其中還包含一些有趣的討論:https://www.quora.com/topic/Machine-Learning |
| Stack Exchange | Stack Exchange系列站點托管用于機器學習問題的多個子域。 |
– _“斯坦福大學的吳安德教授教授的一本優秀的免費在線機器學習課程”:https://www.coursera.org/learn/machine-learning
– _“另一種出色的免費在線課程,采用了更通用的人工智能方法”:https://www.udacity.com/course/intro-to-artificial-intelligence–cs271
