1.17 神經網絡模型(有監督)?

警告：此實現不適用于大規模數據應用。 特別是 scikit-learn 不支持 GPU。如果想要提高運行速度并使用基于 GPU 的實現以及為構建深度學習架構提供更多靈活性的框架，請看 Related Projects

1.17.1 多層感知機

多層感知機(MLP)是一種有監督學習算法，通過在數據集上訓練來學習函數。其中是輸入的維數， 是輸出的維數。給定一組特征和標簽， 它可以對分類或者回歸學習一個非線性函數。與邏輯回歸不同，在輸入層和輸出層之間， 會存在一個層或者多層的非線性層， 稱為隱藏層。圖1展示了一個帶有標量輸出的單層隱藏層的MLP。

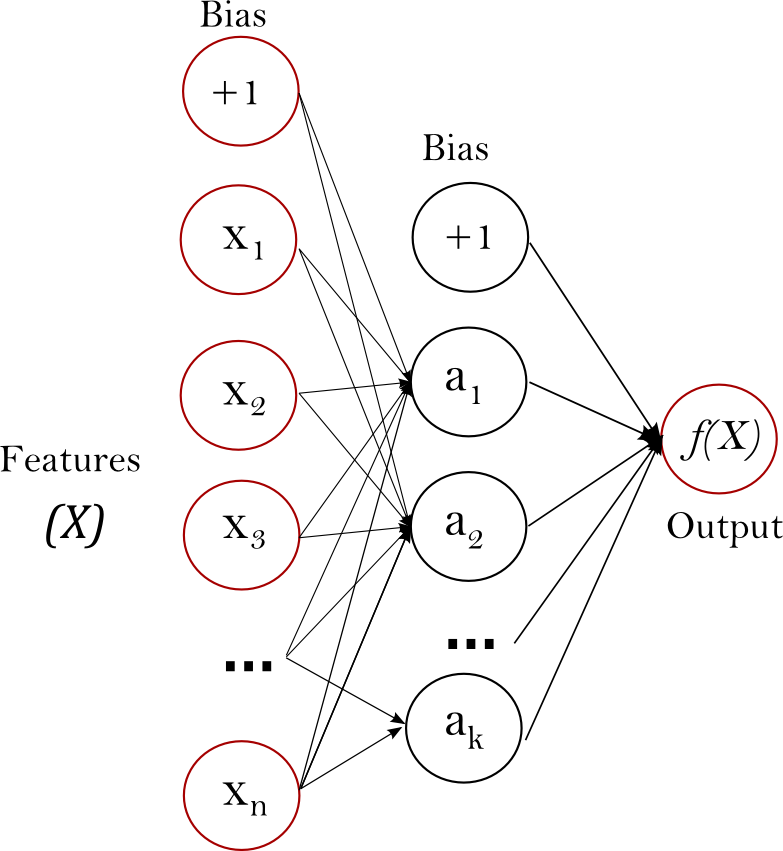? 圖1：單隱藏層MLP.

最左邊的層叫做輸入層， 由一組代表輸入特征的神經元組成。每個隱藏層中的神經元將前一層的值進行加權線性求和轉換, 接著通過非線性函數, 就像雙曲正切函數。輸出層接受的值是最后一個隱藏層經過變換輸出的值。

該模塊下， 包含了公共的屬性 coefs_ 和 intercepts_ 。 coefs_是一個權重矩陣的列表， 其中索引為的權重矩陣表示的第層和第層之間的之間的權重。intercepts_是偏置向量的列表， 其中索引為的向量表示的是添加到底層的偏置值。

多層感知機的優點是：

  • 學習非線性模型的能力。
  • 有使用 partial_fit在實時(在線學習)學習模型的能力。

多層感知機(MLP)的缺點包括：

  • 具有隱藏層的 MLP 具有非凸的損失函數，它有不止一個的局部最小值。 因此不同的隨機初始化權重會導致不同的驗證集準確率。
  • MLP 需要調試一些超參數，例如隱藏層神經元的數量、層數和迭代輪數。
  • MLP對特征縮放是敏感的。

克服這些缺點的方法請參閱 實用使用技巧 部分。

1.17.2 分類

MLPClassifier類通過使用 Backpropagation進行訓練實現了多層感知機（MLP）算法。

MLP 在兩個數組上進行訓練：大小為 (n_samples, n_features) 的數組 X，用來儲存表示訓練樣本的浮點型特征向量; 大小為 (n_samples,) 的數組 y，用來儲存訓練樣本的目標值（類別標簽）：

>>> from sklearn.neural_network import MLPClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
...                     hidden_layer_sizes=(5, 2), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(5, 2), random_state=1,
              solver='lbfgs')

經過擬合(訓練)，該模型可以預測新樣品的標簽：

>>> clf.predict([[2., 2.], [-1., -2.]])
array([1, 0])

MLP可以擬合訓練數據的非線性模型。clf.coefs_包含構成模型參數的權重矩陣：

>>> [coef.shape for coef in clf.coefs_]
[(2, 5), (5, 2), (2, 1)]

目前， MLPClassifier 只支持交叉熵損失函數（ Cross-Entropy loss function），它通過運行 predict_proba 方法進行概率估計。

MLP 算法使用的是反向傳播的方式。 更準確地說，它使用了某種形式的梯度下降來進行訓練，其中的梯度是通過反向傳播計算得到的。 對于分類問題而言，它最小化了交叉熵損失函數，為每個樣本 給出一個向量形式的概率估計 。

>>> clf.predict_proba([[2., 2.], [1., 2.]])
array([[1.967...e-04, 9.998...-01],
       [1.967...e-04, 9.998...-01]])

MLPClassifier通過應用 Softmax作為輸出函數來支持多分類。

此外，該模型支持 multi-label classification，其中一個樣本可以屬于多個類別。 對于每個種類，原始輸出經過 logistic 函數變換后，大于或等于 0.5 的值將為 1，否則為 0。 對于樣本的預測輸出，值為 1 的索引表示該樣本的分類類別：

>>> X = [[0., 0.], [1., 1.]]
>>> y = [[0, 1], [1, 1]]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
...                     hidden_layer_sizes=(15,), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(15,), random_state=1,
              solver='lbfgs')
>>> clf.predict([[1., 2.]])
array([[1, 1]])
>>> clf.predict([[0., 0.]])
array([[0, 1]])

更多內容請參閱下面的示例和文檔 MLPClassifier.fit。

示例
比較MLPClassifier的隨機學習策略
MLP權重在MNIST上的可視化

1.17.3 回歸

類 MLPRegressor實現了一個多層感知器(MLP)，它使用反向傳播來訓練, 輸出層中沒有激活函數，這也可以看作是使用identity function作為激活函數。因此，它使用平方誤差作為損失函數，輸出是一組連續值。

MLPRegressor 還支持多輸出回歸，其中一個樣本可以有多個目標。

1.17.4 正則化

MLPRegressor 和 MLPClassifier 都使用參數alpha進行正則化(L2正則化)，這有助于通過懲罰大規模的權重來避免過度擬合。下面的圖顯示不同alpha值的決策函數。

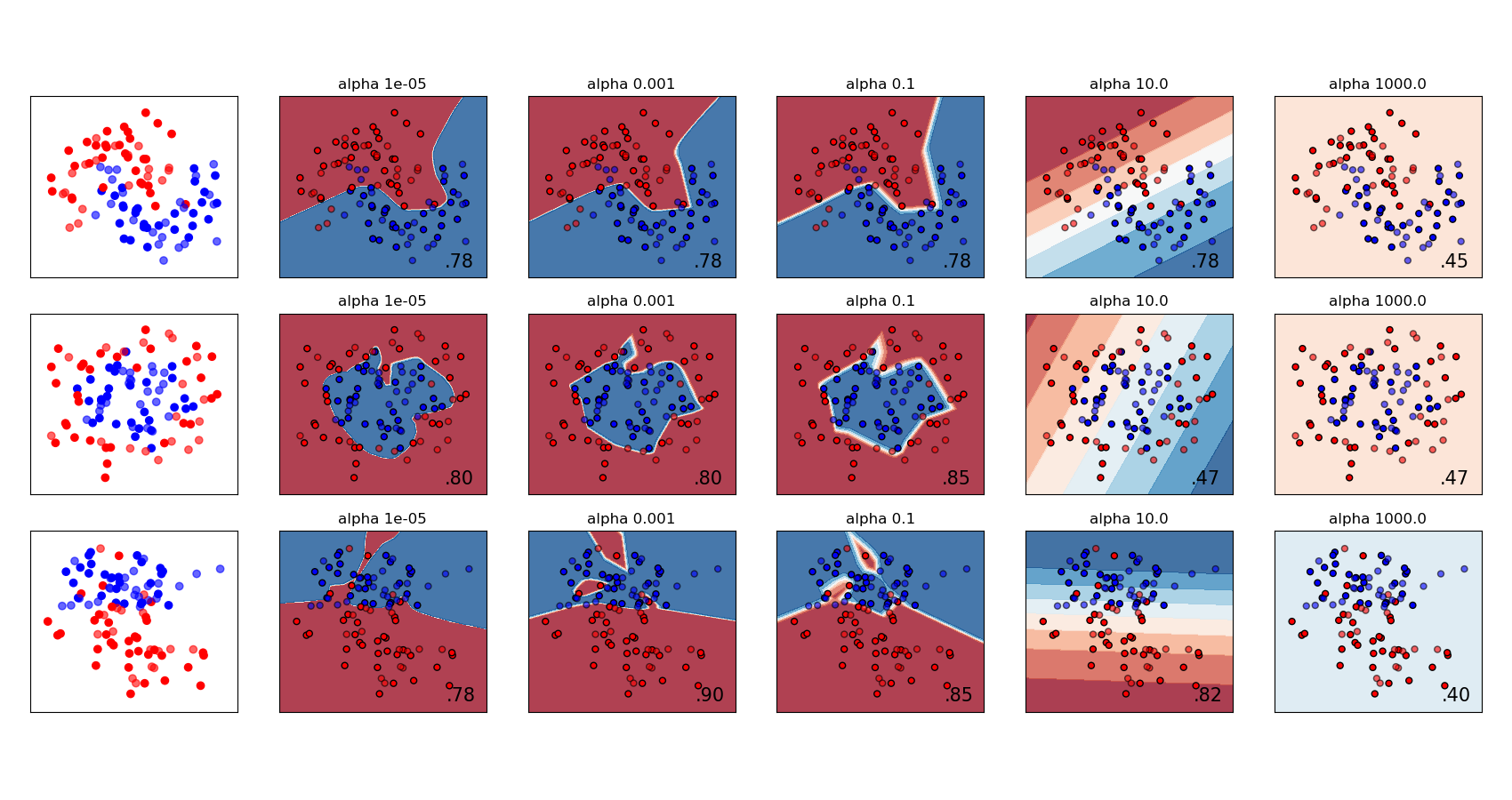有關更多信息，請參見下面的示例。

示例
多層感知器中的正則化

1.17.5 算法

MLP使用隨機梯度下降(Stochastic Gradient Descent)， Adam或者 L-BFGS來進行訓練。隨機梯度下降(SGD)根據需要調整的參數使用損失函數的梯度更新參數，即

其中是控制參數空間搜索步長的學習速率。是神經網絡的損失函數。

更詳細的信息可以在SGD的文檔中找到。

ADAM在某種意義上類似于SGD，它是一個隨機優化器，但它可以根據對低階矩的自適應估計自動調整更新參數的數量。

使用 SGD 或 Adam ，訓練過程可以支持在線學習模式和小批量學習模式。

L-BFGS是一個近似Hessian矩陣的求解器，它表示函數的二階偏導數。此外，它逼近Hessian矩陣的逆以執行參數更新。該實現使用了 L-BFGS的Scipy版本。

如果你所選擇的方法是 ‘L-BFGS’，訓練過程不支持在線學習模式和小批量學習模式。

1.17.6 復雜度

假設有個訓練樣本，個特征，個隱藏層，每個層都包含神經元--為了簡單起見，還有個輸出神經元。反向傳播的時間復雜度為，其中為迭代次數。由于反向傳播具有很高的時間復雜度，最好從較小數量的隱神經元和較少的隱藏層開始進行訓練。

1.17.7 數學公式

給定一組訓練樣本, 其中和，一個隱藏層中一個神經元學習函數是，其中和是模型的參數。分別表示輸入層和隱藏層的權重；分別表示添加到隱藏層和輸出層的偏差。是激活函數，默認設置為（雙曲正切）tan, 它被給出如下：

對于二分類，通過logistic函數獲得0到1之間的輸出值。設置閾值為0.5， 會將大于或等于0.5的輸出樣本分配給正類，其余的分配給負類。

如果有兩個以上的類， 本身將是大小為(n_classes)的向量。它不是通過logistic函數，而是通過Softmax函數，該函數被編寫為，

其中 表示Softmax輸入的第個元素，它對應于第類，是類的數量。結果是包含樣本屬于每個類的概率的向量。輸出是概率最高的類。

在回歸中，輸出保持為 ；因此，輸出激活函數就是恒等函數( identity function)。

MLP根據問題類型使用不同的損失函數。分類損失函數是交叉熵(Cross-Entropy)，在二分類情況下給出如下：

其中，是對模型的復雜度進行懲罰的L2正則化項(也稱為懲罰項)，并且是一個非負的超參數，它控制著懲罰的程度。

對于回歸，MLP使用均方誤差損失函數， 寫成；

從初始隨機化權重開始，多層感知機(MLP)通過重復更新這些權重，使損失函數最小化。在計算損失后，反向傳遞將其從輸出層傳播到前一層，為每個權重參數提供一個更新值，以減少損失。

在梯度下降中，計算得到損失函數關于每個權重的梯度, 并從減去，這可以表示為：

其中是迭代步驟，是值大于0的學習速率。

該算法在達到預定的最大迭代次數，或者當損失的改進低于某個很小的數時停止。

1.17.8 實用技巧

  • 多層感知機對特征的縮放是敏感的，所以它強烈建議您標準化您的數據。 例如，將輸入向量 X 的每個屬性放縮到到 [0, 1] 或 [-1，+1] ，或者將其標準化使它具有 0 均值和方差 1。注意，為了得到有意義的結果，您必須對測試集也應用相同的尺度縮放。 您可以使用 StandardScaler 進行標準化。

    >>> from sklearn.preprocessing import StandardScaler  # doctest: +SKIP
    >>> scaler = StandardScaler()  # doctest: +SKIP
    >>> # Don't cheat - fit only on training data
    >>> scaler.fit(X_train)  # doctest: +SKIP
    >>> X_train = scaler.transform(X_train)  # doctest: +SKIP
    >>> # apply same transformation to test data
    >>> X_test = scaler.transform(X_test)  # doctest: +SKIP

    另一個推薦的方法是在 Pipeline 中使用的 StandardScaler 。

  • 最好使用 GridSearchCV 找到一個合理的正則化參數 ，通常范圍是在 10.0 ** -np.arange(1, 7)

  • 據經驗可知，我們觀察到 L-BFGS是收斂速度更快的且在小數據集上表現更好的解決方案。對于規模相對比較大的數據集， Adam是非常魯棒的。 它通常會迅速收斂，并得到相當不錯的表現。另一方面，如果學習率調整得正確， 使用 momentum 或 nesterov’s momentum 的 SGD可能比這兩種算法更好。

1.17.9 warm_start的更多控制

如果您希望更多地控制SGD中的停止標準或學習速率，或者希望進行額外的監視，那么使用warm_start=True和max_iter=1并迭代自己可能會有幫助：

>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(hidden_layer_sizes=(15,), random_state=1, max_iter=1, warm_start=True)
>>> for i in range(10):
...     clf.fit(X, y)
...     # additional monitoring / inspection
MLPClassifier(...

參考