1.5 隨機梯度下降?

隨機梯度下降(SGD)是一種在凸損失函數(如(線性)支持向量機和Logistic回歸)下擬合線性分類器和回歸器的簡單而有效的方法。盡管SGD在機器學習社區中已經存在了很長一段時間，但就在最近大規模學習的背景下，它得到了相當多的關注。

SGD已成功地應用于文本分類和自然語言處理中經常遇到的大規模和稀疏的機器學習問題。由于數據稀疏，本模塊中的分類器很容易處理到具有個訓練樣本和個特征以上的問題。

嚴格地說，SGD只是一種優化技術，并不與特定的機器學習模型相對應。它只是訓練模型的一種方式。通常，scikit-learn API中SGDClassifier或SGDRegressor 具有等效的估計，只是可能使用了不同的優化技巧。例如，使用SGDClassifier(loss='log')將導致Logistic回歸， 即一個等價于LogisticRegression的模型可以通過SGD擬合而不是LogisticRegression中其他的優化方案。類似的。SGDRegressor(loss='squared_loss', penalty='l2')和 Ridge就是通過不同的方法解決了相同的優化問題。

隨機梯度下降的優點是：

  • 高效
  • 易于實現 (有大量優化代碼的機會)

隨機梯度下降的缺點包括：

  • SGD需要一些超參數，例如正則化參數和迭代次數
  • SGD對特征縮放非常敏感

警告：

在擬合模型之前，一定要重新排序(打亂的)訓練數據，或者在每次迭代后(默認情況下使用)使用shuffle=True來打亂數據。此外，理想情況下，應該使用make_pipeline(StandardScaler(), SGDClassifier())(參見 Pipelines)對特征進行標準化。

1.5.1 分類

SGDClassifier 分類器實現了一個簡單的隨機梯度下降學習程序，支持不同的損失函數和懲罰項。下面是用合頁損失(hinge loss)訓練的SGDClassifier分類器的決策邊界，相當于線性支持向量機。

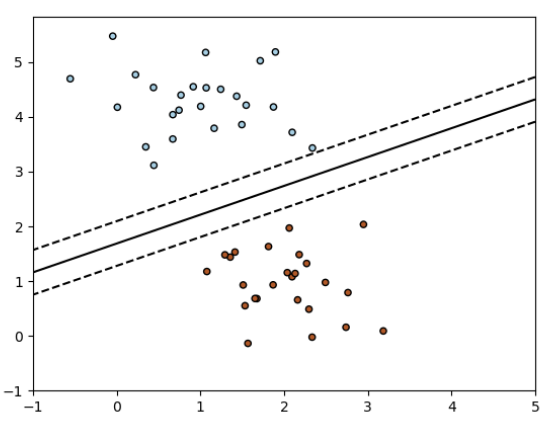作為其他分類器，SGD必須fit兩個數組：一個包含訓練樣本的形狀(n_samples, n_features) 的X和一個包含訓練樣本目標值(類標簽)的形狀 (n_samples)的數組y。

>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
>>> clf.fit(X, y)
SGDClassifier(max_iter=5)

經擬合后，該模型可用于預測新的值：

>>> clf.predict([[2., 2.]])
array([1])

SGD擬合訓練數據的線性模型。coef_屬性保存了模型參數：

>>> clf.coef_
array([[9.9..., 9.9...]])

intercept_保存了截距項(又被稱為 偏移(offset)或者偏差(bias))

>>> clf.intercept_
array([-9.9...])

模型是否使用截距項，即有偏的超平面(a biased hyperplane)，是由參數fit_intercept控制的。

到超平面的符號距離(計算為系數和輸入樣本之間的點積，加上截距)可由 SGDClassifier.decision_function:

>>> clf.decision_function([[2., 2.]])
array([29.6...])

可以通過loss參數設置具體的損失函數。SGDClassifier 分類器支持以下損失函數：

  • loss="hinge":(軟-間隔)線性支持向量機
  • loss="modified_huber:平滑的合頁損耗(smoothed hinge loss)
  • loss="log":邏輯回歸
  • 以及以下所有的回歸損失。在這種情況下，目標被編碼為-1或1，并且這個問題被看作是一個回歸問題。然后，預測的類對應于預測目標的符號。

請參閱下面的數學部分的公式。前兩個損失函數是懶惰的，它們只在一個樣本違反邊際約束的情況下更新模型參數，這使得訓練非常有效，并且也可能導致稀疏模型(即更多的零系數)， 即使使用的是L2懲罰。

使用loss="log" 或者 loss="modified_huber" 來激活 predict_proba 方法,這會給每個樣本一個概率估計的向量。

>>> clf = SGDClassifier(loss="log", max_iter=5).fit(X, y)
>>> clf.predict_proba([[1., 1.]])
array([[0.00..., 0.99...]])

具體的懲罰項可以通過penalty參數來設定。SGD支持以下懲罰項：

  • penalty="l2": L2 范數懲罰 在 coef_
  • penalty="l1": L1 范數懲罰 在 coef_
  • penalty="elasticnet": L1和L2的凸組合; (1 - l1_ratio) * L2 + l1_ratio * L1

默認設置為 penalty="l2"。L1懲罰會導致稀疏解，使大部分系數變為零。彈性網[11]在具有高度相關屬性的情況下，解決了L1懲罰的一些不足。參數l1_ratio控制L1和L2懲罰的凸組合。

SGDClassifier分類器通過使用“one versus all” (OVA)方案組合多個二分類器來支持多分類。對于每個類，學習了一個二分類器，該分類器區分該類和所有其他類。在測試時，我們計算每個分類器的置信分數(即到超平面的符號距離)，并選擇置信度分數最高的類。下圖說明了在 iris數據集的OVA方法。虛線表示三個OVA分類器，背景顏色表示由三個分類器決定的的決策面。

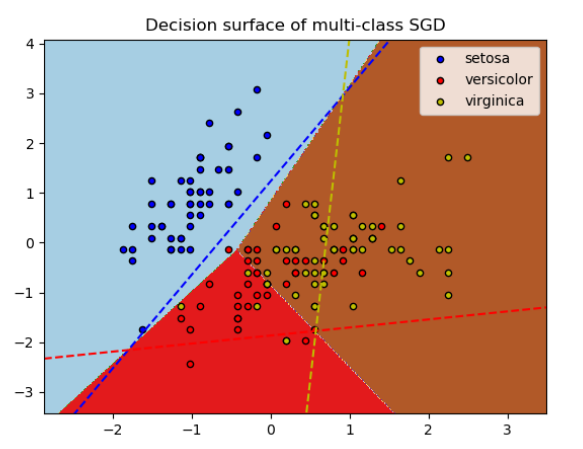在多分類的情況下，coef_是一個形狀是 (n_classes, n_features)的二維數組，而intercept_是一個形狀是(n_classes,)的一維數組。coef_的第i行是第i類的OVA分類器的權重向量；類按升序進行索引(請參見class_)。請注意，原則上，由于它們允許創建概率模型，所以loss="log" 和 loss="modified_huber"更適合于 one-vs-all分類。

SGDClassifier 分類器可以通過fit方法的參數class_weight和sample_weight來支持對類加權和對實例加權。有關更多信息，請參見下面的示例和SGDClassifier.fit的說明文檔。

SGDClassifier支持平均最近梯度下降(averaged SGD (ASGD))[10]。通過設置 average=True來啟用。ASGD與常規的SGD表現出相同的更新(參見數學公式)，但不使用系數的最后一個值作為coef_(即上次更新的值)，相反，coef_被設置為所有更新中系數的平均值。

對于具有邏輯損失的分類，另一種采用平均策略的SGD方法是用隨機平均梯度(SAG)算法進行的，它可以作為 LogisticRegression中的求解器。

示例
SGD:最大間距分離超平面
在iris數據集上繪制多類SGD
SGD:樣本加權
比較各種在線求解器
SVM: 不平衡數據集的分離超平面

1.5.2 回歸

SGDRegressor類實現了一個簡單的隨機梯度下降學習程序，它支持不同的損失函數和懲罰來擬合線性回歸模型。 SGDRegressor非常適合于具有大量訓練樣本(>10.000)的回歸問題，對于其他問題，我們建議使用 Ridge, Lasso, 或者 ElasticNet。

具體的損失函數可以通過 loss 參數設置。 SGDRegressor 支持以下的損失函數:

  • loss="squared_loss": Ordinary least squares(普通最小二乘)
  • loss="huber": Huber loss for robust regression(魯棒回歸的Huber損失)
  • loss="epsilon_insensitive": linear Support Vector Regression(線性支持向量回歸)

有關公式，請參閱下面的數學部分。Huber和epsilon—insensitive損失函數可用于魯棒回歸。不敏感區域的寬度必須通過參數 epsilon 來設定。這個參數取決于目標變量的規模。

penalty參數確定要使用的正則化(請參閱分類部分中的說明)。

SGDRegressor還支持平均SGD [10] (同樣，請參閱分類部分中的說明)。

對于具有平方損失和L2懲罰的回歸，另一種具有平均策略的SGD算法可用隨機平均梯度(SAG)算法作為嶺中的求解器, 就像 Ridge回歸的解法。

1.5.3 稀疏數據的隨機梯度下降

注意：稀疏實現會產生與密集實現略有不同的結果，這是因為學習速率縮小了。請參閱實施細節。

在 scipy.sparse 支持的格式中，任意矩陣都有對稀疏數據的內置支持方法。但是，為了獲得最高的效率，請使用 scipy.sparse.csr_matrix 中定義的 CSR 矩陣格式。

示例
基于稀疏特征的文本分類

1.5.4 復雜度

SGD的主要優點是它的效率，這在訓練數據上基本都是線性的。假如 X 是形狀為 的矩陣，則訓練的成本為, 其中 是迭代次數， 是每個樣本非零特征的平均數。

然而，最近的理論結果表明，隨著訓練集大小的增加，運行時得到一些期望的優化精度并沒有提高。

1.5.5 停止準則

當達到給定的收斂水平時， SGDClassifier和 SGDRegressor提供了兩個停止該算法的準則：

  • 使用早期early_stopping=True，輸入數據被分割成一個訓練集和一個驗證集。然后在訓練集上對模型進行擬合，并根據在驗證集上計算的預測分數(使用分數法)確定停止準則。驗證集的大小可以隨參數validation_fraction而改變。
  • 在early_stopping=False的情況下，模型對整個輸入數據進行擬合，根據目標函數在訓練數據計算確定停止準則。

在這兩種情況下，準則都是按歷次計算一次的，當該準則不改進n_iter_no_change時，該算法就停止了。用絕對公差法進行了評價改進或者算法在最大迭代次數(max_iter)后，這兩種任意一個情況下算法都會停止。

1.5.6 實用技巧

  • 隨機梯度下降對特征縮放非常敏感，因此強烈建議對數據進行縮放。例如，將輸入向量X上的每個特征縮放為[0，1]或[-1，+1]，或將其標準化為均值為0和方差為1。注意，相同的縮放必須應用于測試向量以獲得有意義的結果。使用StandardScaler可以很容易地做到這一點：
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)  # Don't cheat - fit only on training data
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)  # apply same transformation to test data

# Or better yet: use a pipeline!
from sklearn.pipeline import make_pipeline
est = make_pipeline(StandardScaler(), SGDClassifier())
est.fit(X_train)
est.predict(X_test)

如果您的屬性具有固有的尺度(例如，單詞頻率或指示特征)，則不需要縮放。

  • 找到一個合理的正則化項最好是使用自動超參數搜索，比如 GridSearchCV或者RandomizedSearchCV， 通常的范圍是10.0**-np.arange(1,7)

  • 根據經驗，我們發現SGD在觀察了大約10^6個訓練樣本后收斂。因此，對迭代次數的合理猜測是max_iter = np.ceil(10**6 / n)，其中是訓練集的大小。

  • 如果將SGD應用于PCA提取的特征，我們發現，通常明智的做法是將特征值通過某個常數c縮放，使訓練數據的L2范數平均值等于1。

  • 我們發現，當特征很多或 eta0 很大時， ASGD（平均隨機梯度下降） 效果更好。

參考

“Efficient BackProp” Y. LeCun, L. Bottou, G. Orr, K. Müller - In Neural Networks: Tricks of the Trade 1998.

1.5.7 數學公式

我們在這里描述SGD的數學細節。一個很好的概述和收斂速度可以在[12]中找到。

給定一組訓練集樣本, 其中, 分類問題， 我們的目的是得到線性的得分函數, 其中參數, 并且。為了進行二分類預測，我們簡單看一下。為了找到模型參數，我們將正則化訓練誤差降到最小:

其中是度量模型(mis)擬合的損失函數，是懲罰模型復雜度的正則化項，是控制正則化強度的非負超參數。

對于不同的 選擇不同的分類器和回歸器：

  • Hinge (軟間隔)：等價于支持向量分類器

  • Perceptron:

  • Modified Huber:

  • Log: 等價于邏輯回歸：

  • Least-Squares:線性回歸((Ridge 還是 Lasso 取決于 ) 。

  • Huber: 與最小二乘相比，對離群值不太敏感。當, 并且, 等價于最小二乘。

  • Epsilon-Insensitive:(軟間隔)等價于支持向量回歸。

如下圖所示，上述所有損失函數都可視為錯誤分類錯誤(0一1 損失)的上限。

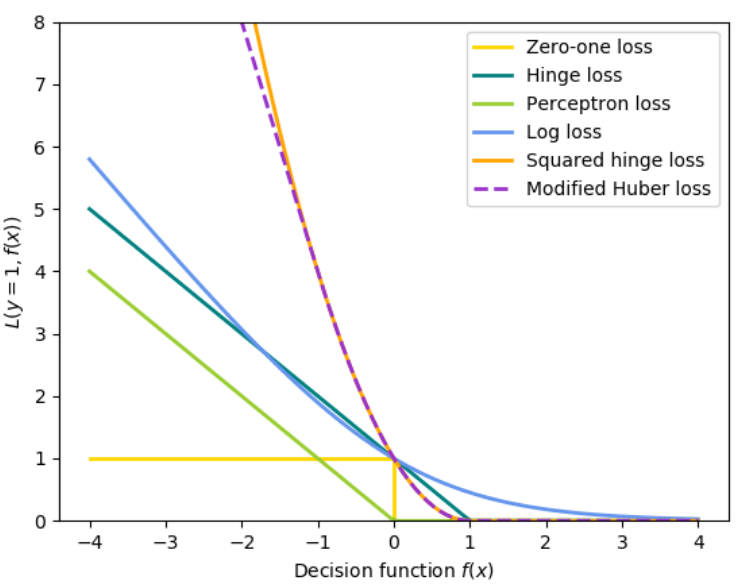比較流行的正則化（penalty 參數）的選擇如下：

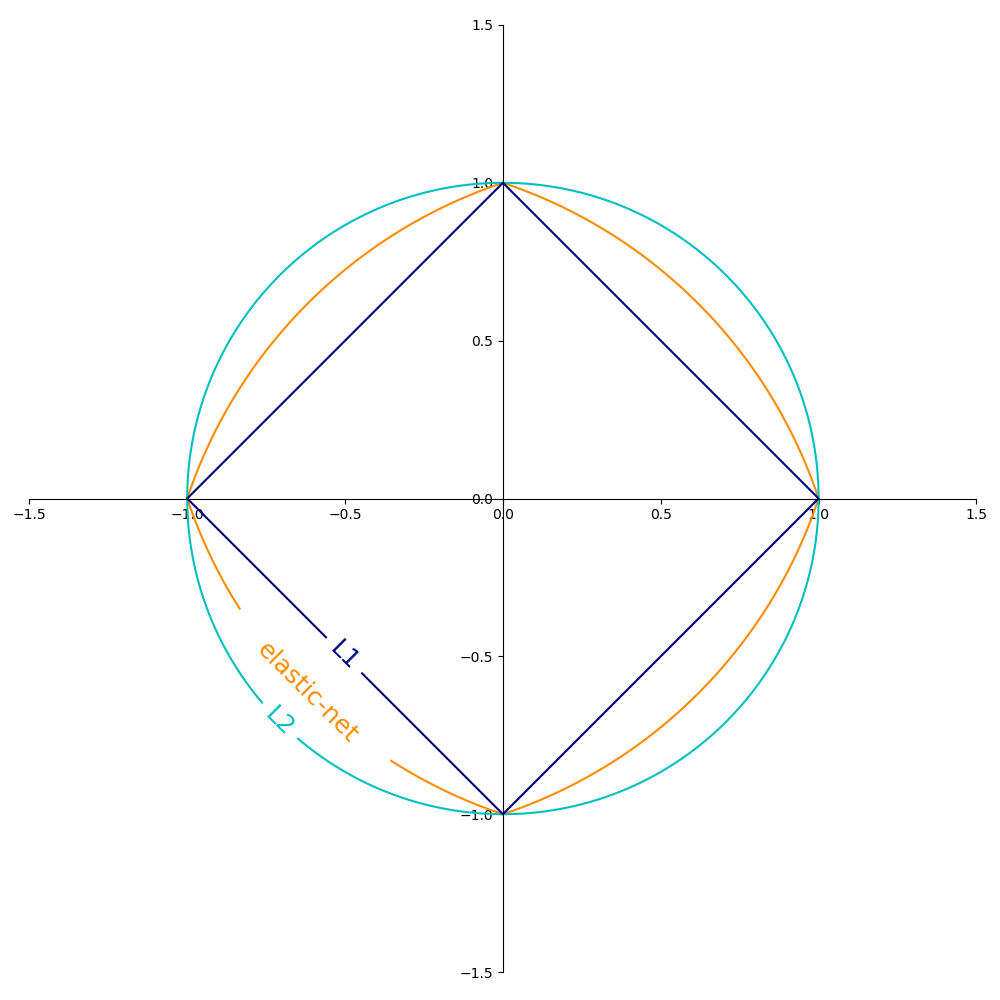
  • L2 范數:
  • L1 范數: 這會導致稀疏的解
  • Elastic Net:, L2和L1的凸組合，其中是通過1 - l1_ratio指定的。

下圖顯示了當=1時，不同正則化項在二維參數空間(=2)中的輪廓。

1.5.7.1 SGD

隨機梯度下降是求解無約束優化問題的一種優化方法。與(批量)梯度下降相比，SGD通過一次只考慮一個訓練樣本來逼近的真實梯度。

SGDClassifier類實現了一階SGD學習程序。該算法對訓練樣本進行迭代，并對每個樣本根據給出的更新規則更新模型參數。

其中 是控制參數空間中學習速率的步長。截距b 類似地被更新，但沒有正則化(并且對稀疏矩陣有額外的衰減，詳見實現細節)。

的學習速率可以是恒定的，也可以是逐漸衰減的。對于分類，默認的學習率通過(learning_rate='optimal')由下式給出。

其中是時間步長(總共有n_samples * n_iter個時間步長)，是基于Léon Bottou提出的啟發式算法確定的，這樣期望的初始更新與權重的預期大小相當(假設訓練樣本的范數接近1)。確切的定義可以在BaseSGD中的的_init_t中找到。

對于回歸，默認的學習率計劃是反向縮放(learning_rate='invscaling')，由下式給出:

其中和是用戶通過 eta0 和power_t指定的超參數。

對于固定的學習速率設置，可以使用learning_rate='constant'，并且通過指定學習率。

對于自適應下降的學習速率，使用learning_rate='adaptive' , 并使用 eta0指定最起始學習速率。當達到停止條件時，學習速率除以5，算法不停止。當學習速率低于1e-6時，算法停止。

模型參數可以通過coef_和intercept_來訪問：coef__持有權重w和intercept__含有b。

當使用平均梯度下降(含有參數average)時, coef_被設置為所有更新的平均權重：coef_=, 其中 是所有更新的總數，可以在屬性t_中找到。

1.5.8 實現細節

SGD 的實現受到[7]的隨機梯度支持向量機的影響。與SvmSGD類似，權重向量表示為標量和向量的乘積，在L2正則化的情況下允許有效的權重更新。在輸入X稀疏的情況下，以較小的學習速率(乘以0.01)更新截距，以說明它被更新得更頻繁。在每個觀察到的示例之后，依次提取訓練示例，并降低學習率。我們采用了[8]中的學習計劃。對于多分類的來說， 采用的是“one versus all”。對于L1正則化(和彈性網)，我們使用了[9]中提出的截斷梯度算法。代碼是用Cython編寫的。

參考資料：

[7] “Stochastic Gradient Descent” L. Bottou - Website, 2010.

[8] “Pegasos: Primal estimated sub-gradient solver for svm” S. Shalev-Shwartz, Y. Singer, N. Srebro - In Proceedings of ICML ‘07.

[9] “Stochastic gradient descent training for l1-regularized log-linear models with cumulative penalty” Y. Tsuruoka, J. Tsujii, S. Ananiadou - In Proceedings of the AFNLP/ACL ‘09.

10(1,2) “Towards Optimal One Pass Large Scale Learning with Averaged Stochastic Gradient Descent” Xu, Wei

[11] “Regularization and variable selection via the elastic net” H. Zou, T. Hastie - Journal of the Royal Statistical Society Series B, 67 (2), 301-320.

[12] “Solving large scale linear prediction problems using stochastic gradient descent algorithms” T. Zhang - In Proceedings of ICML ‘04.