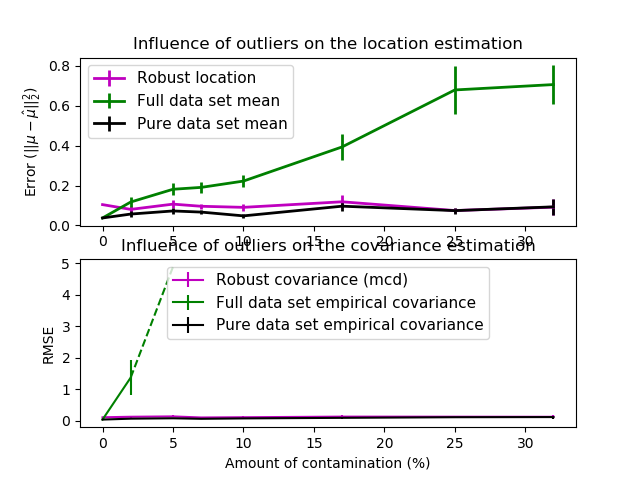
sklearn.covariance.MinCovDet?

class sklearn.covariance.MinCovDet(*, store_precision=True, assume_centered=False, support_fraction=None, random_state=None)

[源碼]

最小協方差決定（MCD）：協方差的穩健估計器。

最小協方差決定估計器適用于高斯分布數據，也可適用于單峰、對稱分布數據。它并不意味著用于多模態數據(用于擬合MinCovDet對象的算法在這種情況下很可能失敗)。我們應該考慮投影追蹤方法來處理多模態數據集。

在用戶指南中閱讀更多內容。

參數	說明
store_precision	bool, default=True 指定是否存儲估計的精度。
assume_centered	bool, default=False 如果為True，則計算穩健位置和協方差估計的支持度，并重新計算協方差估計，而不會先將數據中心化。這在處理均值顯著等于零但不完全為零的數據時很有用。如果為False，則直接使用FastMCD算法計算穩健位置和協方差，而無需進行其他處理。
support_fraction	float, default=None 支持MCD原始估算的點數比例。如果為None，則將在算法中使用support_fraction的最小值：`[n_sample + n_features + 1] / 2`，范圍是（0，1）。
random_state	int or RandomState instance, default=None 確定用于數據混洗的偽隨機數生成器。在多個函數調用之間傳遞同一個整數值以獲得重復的結果。請參閱：`Glossary <random_state>`。

屬性	說明
raw_location_	ndarray of shape (n_features,) 修正和重新加權前的穩健估計位置。
raw_covariance_	ndarray of shape (n_features, n_features) 修正和重新加權之前的原始穩健估計協方差。
raw_support_	ndarray of shape (n_samples,) 在修正和重新加權之前，用于計算位置和形狀的原始穩健估計的觀測數據掩模。
location_	ndarray of shape (n_features,) 估計的穩健位置。
covariance_	ndarray of shape (n_features, n_features) 估計的穩健協方差矩陣。
precision_	ndarray of shape (n_features, n_features) 估計的偽逆矩陣。（僅在store_precision為True時存儲）
support_	ndarray of shape (n_samples,) 用于計算位置和形狀的穩健估計的觀測掩模。
dist_	ndarray of shape (n_samples,) 訓練集（`fit`稱為）觀測值的馬氏距離。

參考

R9f63e655f7bd-Rouseeuw1984 P. J. Rousseeuw. Least median of squares regression. J. Am Stat Ass, 79:871, 1984.

R9f63e655f7bd-Rousseeuw A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS

R9f63e655f7bd-ButlerDavies R. W. Butler, P. L. Davies and M. Jhun, Asymptotics For The Minimum Covariance Determinant Estimator, The Annals of Statistics, 1993, Vol. 21, No. 3, 1385-1400

示例

>>> import numpy as np
>>> from sklearn.covariance import MinCovDet
>>> from sklearn.datasets import make_gaussian_quantiles
>>> real_cov = np.array([[.8, .3],
...                      [.3, .4]])
>>> rng = np.random.RandomState(0)
>>> X = rng.multivariate_normal(mean=[0, 0],
...                                   cov=real_cov,
...                                   size=500)
>>> cov = MinCovDet(random_state=0).fit(X)
>>> cov.covariance_
array([[0.7411..., 0.2535...],
       [0.2535..., 0.3053...]])
>>> cov.location_
array([0.0813... , 0.0427...])

方法

方法	說明
`correct_covariance`(self, data)	對原始的最小協方差行列式估計值進行修正。
`error_norm`(self, comp_cov[, norm, scaling, …])	計算兩個協方差估計量之間的均方誤差。
`fit`(self, X[, y])	用FastMCD算法擬合最小協方差決定。
`get_params`(self[, deep])	獲取此估估算器的參數。
`get_precision`(self)	獲取精度矩陣
`mahalanobis`(self, X)	計算給定觀測值的平方馬氏距離
`reweight_covariance`(self, data)	重新加權原始最小協方差決定估計。
`score`(self, X_test[, y])	使用`self.covariance_`計算高斯數據集的對數似然值，作為其協方差矩陣的估計量。
`set_params`(self, **params)	設置此估算器的參數。

__init__(self, *, store_precision=True, assume_centered=False, support_fraction=None, random_state=None)

[源碼]

初始化self. 請參閱help(type(self))以獲得準確的說明。

correct_covariance(self, data)

[源碼]

對原始的最小協方差決定估計值進行修正。

使用Rousseeuw和Van Driessen在[RVD]中建議的經驗校正因子進行修正。

參數	說明
data	array-like of shape (n_samples, n_features) 用于計算原始估計值的數據集，具有p個特征和n個樣本的數據矩陣。

返回值	說明
covariance_corrected	ndarray of shape (n_features, n_features) 校正的穩健協方差估計。

參考資料

[RVD] Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS

error_norm(self, comp_cov, norm='frobenius', scaling=True, squared=True)

[源碼]

計算兩個協方差估計量之間的均方誤差。（在Frobenius規范的意義上）。

參數	說明
comp_cov	array-like of shape (n_features, n_features) 要比較的協方差。
norm	{“frobenius”, “spectral”}, default=”frobenius” 用于計算誤差的規范類型，可用的誤差類型: - ‘frobenius’ (default): - ‘spectral’: 這里的A是 `(comp_cov - self.covariance_)`的誤差
scaling	bool, default=True 如果為True（默認），則平方誤差范數除以n_features。如果為False，則不會重新調整平方誤差范數。
squared	bool, default=True 是計算平方誤差范數還是誤差范數。如果為True（默認），則返回平方誤差范數。如果為False，則返回誤差范數。

返回值	說明
result	float `self`和`comp_cov`協方差估計量之間的均方誤差（按照Frobenius范式的含義）。

fit(self,X,y = None )

[源碼]

用FastMCD算法擬合最小協方差決定。

參數	說明
X	array-like of shape (n_samples, n_features) 訓練數據，其中`n_samples`是樣本數量，`n_features`是特征數量。
y	Ignored 未使用，出于API一致性目的而存在。

返回值	說明
self	object

get_params(self, deep=True)

[源碼]

獲取此估計量的參數。

參數	說明
deep	bool, default=True 如果為True，則將返回此估算器與其所包含子對象的參數。

返回值	說明
params	mapping of string to any 參數名稱映射到其值。

get_precision(self)

[源碼]

獲取精確度矩陣。

返回值	說明
precision_	array-like of shape (n_features, n_features) 與當前協方差對象關聯的精度矩陣。

mahalanobis(self, X)

[源碼]

計算給定觀測值的平方馬氏距離。

參數	說明
X	array-like of shape (n_samples, n_features) 觀測值，用來計算馬氏距離。假定觀測值與fit中使用的數據來自相同的分布。

返回值	說明
dist	ndarray of shape (n_samples,) 觀測值的平方馬氏距離。

reweight_covariance(self, data)

[源碼]

重新加權原始最小協方差決定的估計值。

使用Rousseeuw在 [RVDriessen]中描述的方法(相當于在計算位置和協方差估計之前從數據集中刪除離群點)重新計算觀測值的權重。

參數	說明
data	array-like of shape (n_samples, n_features) 用于計算原始估計值的數據集，具有p個特征和n個樣本的數據矩陣。

返回值	說明
location_reweighted	ndarray of shape (n_features,) 重新加權的穩健位置估計。
covariance_reweighted	ndarray of shape (n_features, n_features) 重新加權的穩健協方差估計。
support_reweighted	ndarray of shape (n_samples,), dtype=bool 用于計算重新加權的穩健定位和協方差估計的觀測掩模。

參考資料

[RVDriessen] A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS

score(self, X_test, y=None)

[源碼]

使用self.covariance_作為協方差矩陣的估計值來計算高斯數據集的對數似然。

參數	說明
X_test	array-like of shape (n_samples, n_features) 計算似然性的測試數據集，其中n_samples是樣本數，n_features是特征數。假定X_test與擬合（包括中心化）使用的數據來自相同的分布。
y	Ignored 未使用，出于API一致性目的而存在。

返回值	說明
res	float 數據集以`self.covariance_`作為其協方差矩陣的估計量的似然性。

set_params(self, **params)

[源碼]

設置此估計器的參數。

該方法適用于簡單的估計器以及嵌套對象（例如管道）。后者具有形式參數<component>__<parameter>以便可以更新嵌套對象的每個組件。

參數	說明
**params	dict 估算器參數。

返回值	參數
self	object 估算器對象。

sklearn.covariance.MinCovDet使用示例?

魯棒協方差估計與Mahalanobis距離相關性 ?

穩健與經驗協方差估計 ?