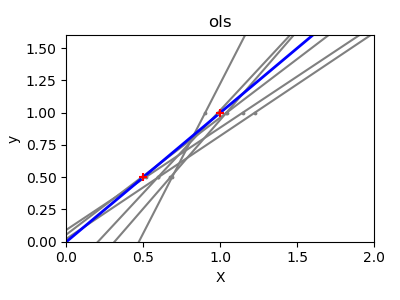
4.1 部分依賴圖?
部分依賴圖( Partial dependence plots ,PDP)顯示了目標響應[1]和一組“目標”特征之間的依賴關系,并邊緣化其他特征(“ 補充(complement) ”特征)的值。直觀地,我們可以將部分依賴關系解釋為預期目標響應與“目標”特征的函數。
由于人類感知的局限性,目標特征集的大小必須很小(通常為一或兩個),因此目標特征通常在最重要的特征中選擇。
下圖利用GradientBoostingRegressor顯示了加利福尼亞住房數據集的四個單向和一個雙向PDP:
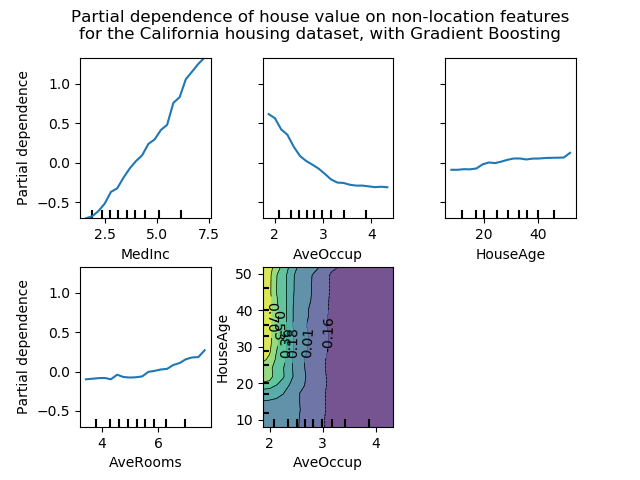 單向PDP告訴我們目標響應和目標特征(例如線性,非線性)之間的相互作用。上圖的左上子圖顯示了一個地區的收入中位數對房價中位數的影響;我們可以清楚地看到它們之間的線性關系。請注意,PDP假設目標特征獨立于互補特征,但是在現實中經常違反此假設。
單向PDP告訴我們目標響應和目標特征(例如線性,非線性)之間的相互作用。上圖的左上子圖顯示了一個地區的收入中位數對房價中位數的影響;我們可以清楚地看到它們之間的線性關系。請注意,PDP假設目標特征獨立于互補特征,但是在現實中經常違反此假設。
具有兩個目標特征的PDP顯示了兩個特征之間的相互作用。例如,上圖中的兩變量PDP顯示了房價中位數對房屋年齡與每戶平均居住者的交互項的依賴性。我們可以清楚地看到這兩個特征之間的相互作用:對于平均入住率大于2的房屋,房價幾乎與房屋年齡無關,而對于小于2的房屋,房價與年齡呈現出強烈的依賴性。
sklearn.inspection模塊提供了一個方便的功能 plot_partial_dependence,可以創建單向和雙向部分依賴圖。在下面的示例中,我們會展示如何創建局部依賴圖的網格:用于0、1特征的單向PDP 以及這兩個特征之間的雙向PDP:
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.inspection import plot_partial_dependence
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1, (0, 1)]
>>> plot_partial_dependence(clf, X, features)
你可以使用plt.gcf()和plt.gca()訪問新創建的figure和axis對象。
對于多類分類,需要通過target參數設置類標簽,來創建PDP:
>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> mc_clf = GradientBoostingClassifier(n_estimators=10,
... max_depth=1).fit(iris.data, iris.target)
>>> features = [3, 2, (3, 2)]
>>> plot_partial_dependence(mc_clf, X, features, target=0)
在多輸出回歸中,可以使用相同的參數target指定目標變量。
如果需要局部依賴函數的原始值而不是圖,可以使用sklearn.inspection.partial_dependence函數:
>>> from sklearn.inspection import partial_dependence
>>> pdp, axes = partial_dependence(clf, X, [0])
>>> pdp
array([[ 2.466..., 2.466..., ...
>>> axes
[array([-1.624..., -1.592..., ...
局部依賴關系的值直接由x生成 。對于雙向部分依賴關系,將生成值的二維網格。由 sklearn.inspection.partial_dependence返回的values參數給出了每個目標特征在網格中使用的實際值。它們還對應于圖形的軸。
4.1.1 數學定義
是目標特征(即features參數)的集合,為其補充特征。
響應的部分依賴 在某一點 上定義為:
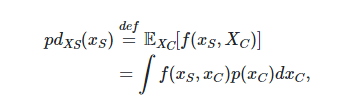 這里 是給定樣本的響應函數(predict, predict_proba或decision_function),樣本中,在和中的特征分別被定義為和 。注意 和 可能是元組。
這里 是給定樣本的響應函數(predict, predict_proba或decision_function),樣本中,在和中的特征分別被定義為和 。注意 和 可能是元組。
對于各種取值計算這個積分,就會產生如上所述的圖。
4.1.2 計算方法
有兩種近似上述積分的主要方法,即“brute”和“recurtion”方法。利用method參數可以控制使用哪種方法。
"brute"方法是可與任何估計器一起使用的通用方法。它通過計算數據的平均值來近似上述積分:
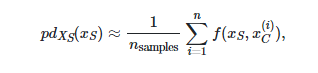 是里的第個樣本特征值。 對于里對的每個值,此方法需要對龐大的數據集進行完全遍歷。
是里的第個樣本特征值。 對于里對的每個值,此方法需要對龐大的數據集進行完全遍歷。
“recurtion”方法比“brute”方法快,但是僅支持某些基于樹的估計器。計算如下,對于給定的特征,執行加權樹遍歷:如果拆分節點涉及“目標”特征,則遵循相應的左分支或右分支;否則,兩個分支都會被跟蹤,每個分支都會按進入該分支的訓練樣本的比例加權。最后,部分依賴關系由所有訪問的葉子節點的加權平均值給出。
使用“ brute”方法時,參數X用于對目標特征,和補充特征值生成值網格。但是,對于“recurtion”方法,該方法X僅用于網格值,是訓練數據的值。
默認情況下,“recurtion”方法用于支持它的基于樹的估計器,其他的估計器則使用“ brute”。
| 注意 |
|---|
| 雖然這兩種方法通常應該很接近,但是在某些特定設置上可能會有所不同。“brute”方法假定存在數據點。當特征相關時,這樣的樣本可能具有非常低的概率質量。“brute”和“recurtion”方法可能會在部分依賴的價值上存在分歧,因為它們將對這些樣本進行不同的處理。但值得注意的是,解釋PDP的主要假設是特征之間應是獨立的。 |
| 腳注 |
|---|
| [1] 對于分類,目標響應可以是某個類別的概率(用于二進制分類的肯定類別)或決策函數。 |
| 例子: |
|---|
| 部分依賴圖 |
| 參考文獻 |
|---|
| T. Hastie,R。Tibshirani和J.Friedman,《統計學習的要素》,第二版,第10.13.2節,Springer,2009年。 C.Molnar,可解釋機器學習,第5.1節,2019年。 |