1.10 決策樹?

決策樹(DTs)是一種用于分類和回歸的非參數有監督學習方法。其目標是創建一個模型，通過學習從數據特性中推斷出的簡單決策規則來預測目標變量的值。

例如，在下面的示例中，決策樹從數據中學習，用一組if-then-else的決策規則來逼近正弦曲線。樹越深，決策規則越復雜，模型越適合。

決策樹的一些優點：

  • 易于理解和解釋。樹可以被可視化。
  • 幾乎不需要數據準備。其他算法通常需要數據標準化，需要創建虛擬變量并刪除缺失值。但是，請注意，此模塊不支持缺失值。
  • 使用樹的成本(即預測數據)是用于訓練樹的數據點數的對數。
  • 能夠處理數值型和分類型數據。其他技術通常專門分析只有一種類型變量的數據集。有關更多信息，請參見algorithms 。
  • 能夠處理多輸出問題。
  • 使用白盒模型。如果給定的情況在模型中是可以觀察到的，那么對條件的解釋就很容易用布爾邏輯來解釋。相反，在黑箱模型中(例如，在人工神經網絡中)，結果可能很難解釋。
  • 可以使用統計測試驗證模型。這樣就有可能對模型的可靠性作出解釋。
  • 即使它的假設在某種程度上被生成數據的真實模型所違背，它也表現得很好。

決策樹的缺點包括：

  • 決策樹學習器可以創建過于復雜的樹，不能很好地概括數據。這就是所謂的過擬合。為了避免這個問題，必須設置剪枝、設置葉節點所需的最小樣本數或設置樹的最大深度等機制。

  • 決策樹可能是不穩定的，因為數據中的小變化可能導致生成完全不同的樹。通過集成決策樹來緩解這個問題。

  • 學習最優決策樹的問題在最優性的幾個方面都是NP-complete的，甚至對于簡單的概念也是如此。因此，實際的決策樹學習算法是基于啟發式算法，如貪婪算法，在每個節點上進行局部最優決策。這種算法不能保證返回全局最優決策樹。這可以通過訓練多棵樹再集成一個學習器來緩解，其中特征和樣本被隨機抽取并替換。

  • 有些概念很難學習，因為決策樹不能很容易地表達它們，例如異或、奇偶校驗或多路復用器問題。

  • 如果某些類占主導地位，則決策樹學習者會創建有偏見的樹。因此，建議在擬合決策樹之前平衡數據集。

1.10.1 分類

DecisionTreeClassifier 是一個能夠在數據集上執行多類分類的類。

與其他分類器一樣，DecisionTreeClassifier使用兩個數組作為輸入：形狀為[n_samples, n_features]的數組(稀疏或稠密)，以及整數值數組，形狀[n_samples]，保存訓練樣本的類標簽：

>>> from sklearn import tree
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)

經擬合后，該模型可用于預測其他樣本的類別：

>>> clf.predict([[2., 2.]])
array([1])

或者，可以預測屬于每一類別的概率，即同一類的訓練樣本在一片葉子中的分數：

>>> clf.predict_proba([[2., 2.]])
array([[0., 1.]])

DecisionTreeClassifier 既能夠進行二分類(其中標簽為[-1，1])，也能夠進行多類分類(其中標簽為[0，…K-1])分類。

使用Iris數據集，我們可以構建如下樹：

>>> from sklearn.datasets import load_iris
>>> from sklearn import tree
>>> X, y = load_iris(return_X_y=True)
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, y)

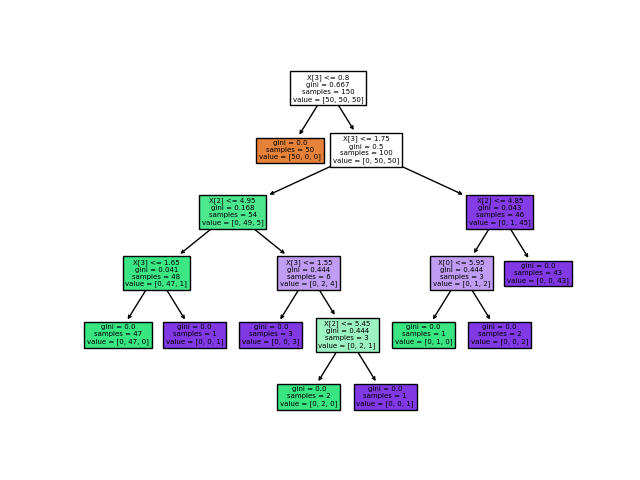
一旦經過訓練，就可以用 plot_tree函數繪制樹：

>>> tree.plot_tree(clf) 

我們還可以使用 export_graphviz導出器以 Graphviz 格式導出樹。如果使用 conda包管理器，則可以使用 conda install python-graphviz安裝Graphviz二進制文件和python包。

另外，還可以從Graphviz項目主頁下載用于Graphviz的二進制文件，并從pypi使用 pip install graphviz安裝Python包裝器并安裝Graphviz。

下面是對整個 iris 數據集進行訓練的樹的圖形輸出示例；結果保存在一個輸出文件iris.pdf中：

>>> import graphviz 
>>> dot_data = tree.export_graphviz(clf, out_file=None) 
>>> graph = graphviz.Source(dot_data) 
>>> graph.render("iris") 

export_graphviz 還支持各種美化，包括通過他們的類著色節點（或回歸值），如果需要，還能使用顯式變量和類名。Jupyter notebook也可以自動內聯式渲染這些繪制節點:

>>> dot_data = tree.export_graphviz(clf, out_file=None, 
...                      feature_names=iris.feature_names,  
...                      class_names=iris.target_names,  
...                      filled=True, rounded=True,  
...                      special_characters=True)  
>>> graph = graphviz.Source(dot_data)  
>>> graph 

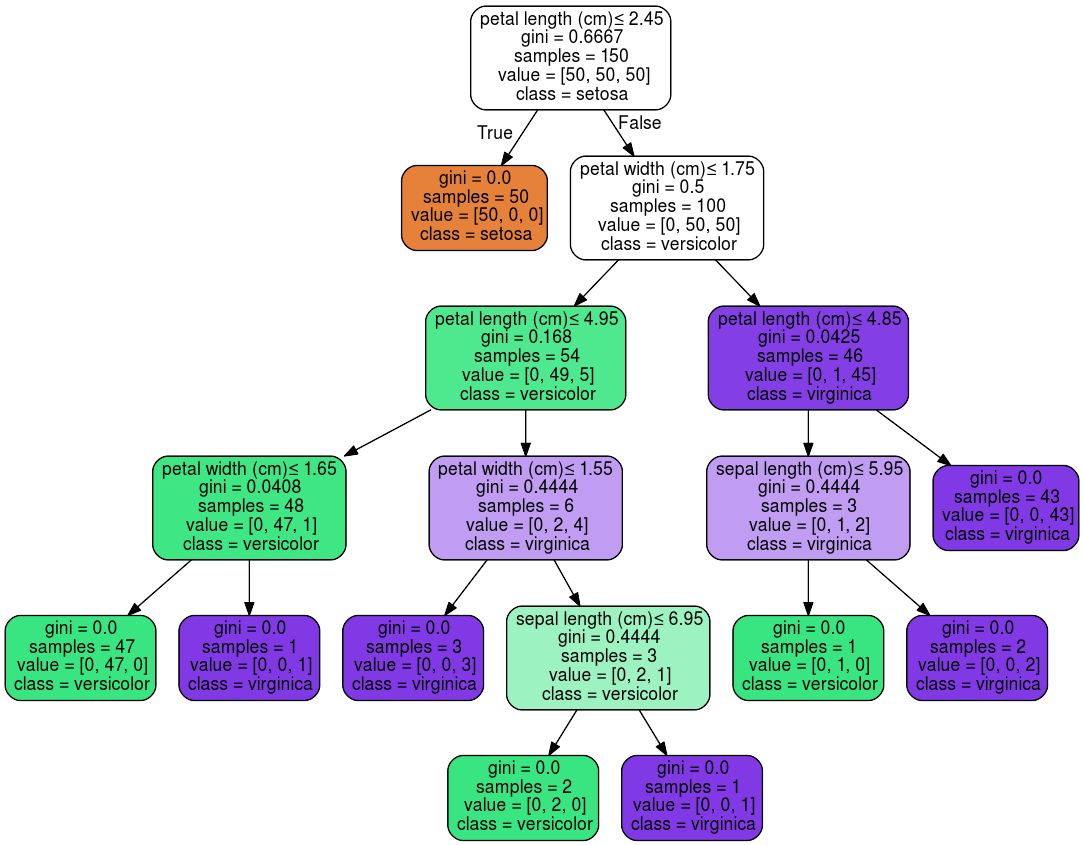
或者，還可以使用函數 export_text以文本格式導出樹。此方法不需要安裝外部庫，而且更緊湊：

>>> from sklearn.datasets import load_iris
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.tree import export_text
>>> iris = load_iris()
>>> decision_tree = DecisionTreeClassifier(random_state=0, max_depth=2)
>>> decision_tree = decision_tree.fit(iris.data, iris.target)
>>> r = export_text(decision_tree, feature_names=iris['feature_names'])
>>> print(r)
|--- petal width (cm) <= 0.80
|   |--- class: 0
|--- petal width (cm) >  0.80
|   |--- petal width (cm) <= 1.75
|   |   |--- class: 1
|   |--- petal width (cm) >  1.75
|   |   |--- class: 2
<BLANKLINE>
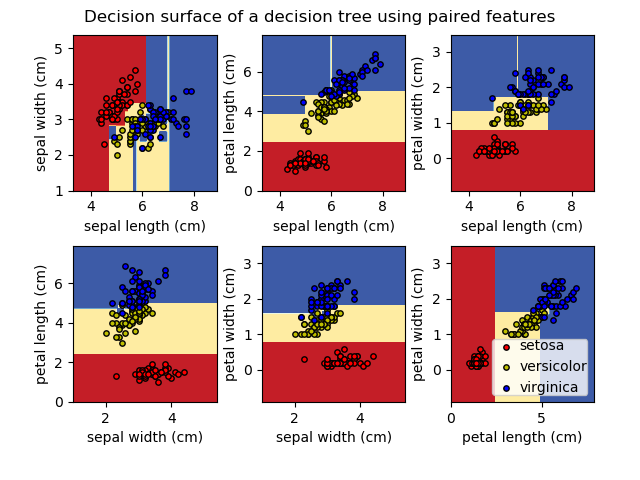
示例
在iris數據集中繪制決策樹的決策面
理解決策樹結構

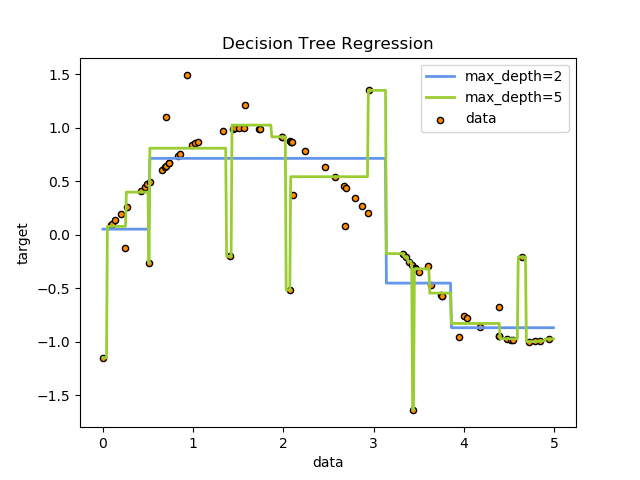
1.10.2 回歸

決策樹也可以應用于回歸問題，使用DecisionTreeRegressor 類。

與分類的設置一樣，fit方法需要參數數組X和y，只是在這種情況下，y可以有浮點數值，而不是整數值：

>>> from sklearn import tree
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])
示例
決策樹回歸

1.10.3 多輸出問題

多輸出問題是一個具有多個輸出預測的有監督學習問題，即 Y 是一個大小為二維的數組[n_samples, n_outputs]。

當輸出之間沒有相關性時，解決這類問題的一個非常簡單的方法是建立n個獨立的模型，即對于每個輸出，利用這些模型獨立地預測n個輸出的每一個。但是，由于可能由于輸出的值與同樣的輸入本身是相關的，所以通常更好的方法是建立一個能夠同時預測所有n個輸出的單一模型。首先，它需要較低的訓練時間，因為只需要建立一個簡單的估計器。其次，估計結果的泛化精度往往會提高。

對于決策樹，這種策略可以很容易地用于支持多輸出問題。這需要進行以下更改：

  • 將n個輸出值存儲在葉子中，而不是1；
  • 通過計算所有n個輸出的平均減少量來作為分裂標準。

該模塊通過在 DecisionTreeClassifier 和DecisionTreeRegressor 中實現該策略來支持多輸出問題。如果一個決策樹在形狀為 [n_samples, n_outputs] 的輸出數組Y上進行擬合，則得到的估計器:

  • predict輸出的是 n_output 的值;
  • 在predict_proba上輸出類概率數組n_output的列表。

多輸出決策樹回歸中說明了多輸出樹在回歸上的應用。 在該示例中，輸入X是單個實數值，并且輸出Y是X的正弦和余弦。

在使用多輸出估算器完成人臉繪制中演示了多輸出樹的分類的使用。在這個例子中，輸入X是人臉的上半部分的像素，輸出Y是這些人臉的下半部的像素。

示例
多輸出決策樹回歸
使用多輸出估算器完成人臉繪制

參考

M. Dumont et al, Fast multi-class image annotation with random subwindows and multiple output randomized trees, International Conference on Computer Vision Theory and Applications 2009

1.10.4 復雜度

通常，構建平衡二叉樹的運行時間代價是和查詢時間是。雖然樹構造算法試圖生成平衡樹，但它們并不總是平衡的。假設子樹保持近似平衡，每個節點的代價成本是通過搜索找到熵減少最大的特征。這在每個節點上的成本為，導致整個樹的總成本(通過將每個節點的成本求和)是。

1.10.5 實用技巧

  • 對于擁有大量特征的數據決策樹會趨向于過擬合。獲得一個合適的樣本與特征的比例十分重要，因為具有高維空間中只有少量的樣本的， 那樹是十分容易過擬合的。

  • 考慮在此之前進行降維((PCA, ICA, 或者 Feature selection) )，以便給您的樹更好的機會找到更有區分度的特征。

  • 通過 export 功能可以可視化您的決策樹。使用 max_depth=3 作為初始樹深度，讓決策樹知道如何適應您的數據，然后再增加樹的深度。

  • 了解決策樹結構理解決策樹的結構 將有助于更深入地了解決策樹是如何進行預測的，這對于理解數據中的重要特性非常重要。

  • 通過 export 功能可以可視化您的決策樹。使用 max_depth=3 作為初始樹深度，讓決策樹知道如何適應您的數據，然后再增加樹的深度。

  • 通過使用 min_samples_split 和 min_samples_leaf 確保多個樣本通知樹中的每個決策， 方法是控制將考慮哪些分割。當這個值很小時意味著生成的決策樹將會過擬合，然而當這個值很大時將會不利于決策樹的對樣本進行學習。嘗試 min_samples_leaf=5 作為初始值。如果樣本的變化量很大，可以使用浮點數作為這兩個參數中的百分比。當min_samples_split 可以產生任意小的葉子時，, min_samples_leaf保證每個葉子都有最小的大小，避免了回歸問題中的低方差、過擬合的葉節點。對于少數類的分類，min_samples_leaf=1通常是最好的選擇。

  • 在訓練前平衡數據集，以防止樹偏向于占主導地位的類。類平衡可以通過從每個類中抽取相同數量的樣本來實現，或者最好通過將每個類的樣本權重(sample_weight)之和歸一化為相同的值來實現。還要注意的是，基于權重的預剪枝準則(如 min_weight_fraction_leaf)將比不知道樣本權重的標準(如min_samples_leaf)更傾向于優勢類。

  • 如果樣本是加權的，則使用基于權重的預剪枝準則(如min_weight_fraction_leaf)來優化樹結構，這樣可以確保葉節點至少包含樣本權重的總和的一部分。

  • 所有決策樹都在內部使用np.float32數組。如果訓練數據不是這種格式，則將復制數據集。

  • 如果輸入矩陣X非常稀疏，則建議在調用fit方法之前將其轉換為稀疏 csc_matrix，在調用predict之前將其轉換為稀疏csr_matrix。當大多數樣本的特征值為零時，輸入的稀疏矩陣訓練時間比密集矩陣的訓練時間快幾個數量級。

1.10.6 樹算法：ID3、C4.5、C5.0和CART

各種決策樹算法是什么？它們之間有何不同？哪一種是在scikit-learn中實現的？

ID3(迭代分離 3)是由Ross Quinlan于1986年開發的。該算法建立了一個多路樹，為每個節點(即貪婪地)尋找分類特征，從而為分類目標提供最大的信息增益。樹生長到它們的最大尺寸，然后，通常采取一個剪枝步驟，以提高樹的對位置數據的泛化能力。

c4.5是ID3的繼承者，并且通過動態定義將連續屬性值分割成一組離散間隔的離散屬性（基于數字變量），從而消除了特征必須是分類的限制。c4.5將經過訓練的樹(即ID3算法的輸出)轉換成一組if-then規則的集合。然后對每條規則的這些準確性進行評估，以確定應用它們的順序。如果規則的準確性沒有提高的話，則需要決策樹的樹枝來解決。

c5.0是Quinlan在專有許可下發布的最新版本。與C4.5相比，它使用更少的內存和構建更小的規則集，同時更精確。

CART (分類和回歸樹)與C4.5非常相似，但它的不同之處在于它支持數值目標變量(回歸)，不計算規則集。CART使用特征和閾值構造二叉樹，在每個節點上獲得最大的信息增益。

scikit-learn使用 CART算法的優化版本；但是目前，scikit-learn實現不支持分類變量。

1.10.7 數學公式

給定訓練向量 I和標簽向量，決策樹遞歸地劃分空間，使得具有相同標簽的樣本被分到一樣的組。

讓節點處的數據集用表示，對于一個由特征和閾值組成的候選劃分數據集，將數據劃分為和兩個子集。

節點處的不存度用不存度函數計算，其選擇取決于正在解決的任務(分類或回歸)。

選擇使不存度最小化的參數

對子集進行遞歸，直到達到最大允許的深度，。

1.10.7.1 分類標準

如果目標是變量的值0，1，…K-1的分類結果，對于節點，表示具有個觀測值的區域，令：

表示的是節點中k類觀測的比例。

常見的不存度度量的方法是 Gini

熵(Entropy)

和錯誤分類（Misclassification）

其中是節點中的訓練數據。

1.10.7.2 回歸標準

如果目標是連續性的值，那么對于節點 ,表示具有 個觀測值的區域 ，對于以后的分裂節點的位置的決定常用的最小化標準是均方誤差和平均絕對誤差，前者使用終端節點處的平均值來最小化L2誤差，后者使用終端節點處的中值來最小化 L1 誤差。

均方誤差：

平均絕對誤差：

其中是節點中的訓練數據。

1.10.8 最小成本復雜度剪枝

最小代價復雜度剪枝是一種用于修剪樹以避免過擬合的算法，在[BRE]第3章中描述了這種算法。該算法由作為復雜度參數進行參數化。復雜度參數用于定義給定樹的成本復雜度度量：

其中，是中的終端節點數，傳統上定義為終端節點的總誤分類率。或者，scikit-learn使用終端節點的總樣本加權不存度作為。如上所述，節點的不存度取決于標準(criterion)。最小成本-復雜度剪枝找到的子樹，使最小化。

單節點的代價復雜度度量為 。被定義為一棵樹，其中分支節點是它的根。一般而言，節點的不存度大于其葉子節點的不存度之和，。然而，節點及其分支 的成本復雜度度量取決于。我們定義了一個節點的有效為與它們相等的值， 或者。一個非葉子節點，其最小的是最弱的連接(weakest link)，并將被修剪。當被剪枝的樹的最小的比ccp_alpha參數大時，此過程將停止。

示例
具有成本復雜度的后剪枝決策樹

參考

[BRE] L. Breiman, J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Wadsworth, Belmont, CA, 1984.