1.11 集成算法?
集成算法的目的是將幾個基估計器的預測與給定的學習算法結合起來,以提高單個估計器的通用性和魯棒性。
集成方法一般分為兩種:
在平均法(averaging methods)中,該方法的原理是構建多個獨立的估計器,然后取它們的預測結果的平均。一般來說,組合之后的估計器是會比單個估計器要好的,因為它的方差減小了。
相反,在提升法(boosting methods)中,基估計器是按順序建立的,并且試圖減小組合估計器的偏差。其動機是將幾個弱模型結合起來,形成一個強大的整體。
示例: AdaBoost, Gradient Tree Boosting, …
1.11.1 Bagging meta-estimator(Bagging 元-估計器)
在集成算法中, bagging方法形成了一類算法,它在原始訓練集的隨機子集上建立幾個黑箱估計器的實例,然后將它們的個體預測聚合起來,形成最終的預測。這些方法通過在基本估計器(例如決策樹)的構造過程中引入隨機化,然后將其集成起來,從而降低單個基本估計器(如決策樹)的方差。在許多情況下,bagging方法是一個非常簡單的方法可以用來改進相對單一模型,而不需要調整底層。由于bagging方法提供了一種減少過度擬合的途徑,因此對強大模型和復雜模型(例如,充分生長的決策樹)最有效,與之對比的提升法在弱模型(例如淺層決策樹)上表現最好。
Bagging方法有許多不同的變種(flavours),但主要是因為它們提取訓練集的隨機子集的方式不同:
如果抽取的數據集的隨機子集是樣本的隨機子集,我們叫做粘貼 (Pasting) [B1999] 。 如果樣本抽取是有放回的,我們稱為 Bagging。 [B1996] 如果抽取的數據集的隨機子集是特征的隨機子集,我們叫做隨機子空間 (Random Subspaces) [H1998] 最后,如果基估計器構建在對于樣本和特征抽取的子集之上時,我們叫做隨機補丁 (Random Patches) [LG2012].
在 scikit-learn中, bagging方法都是BaggingClassifier 元估計器(Resp)提供的。(或者BaggingRegressor),基估計器和隨機子集的抽取策略作為參數由用戶指定。特別是, max_samples和max_features控制子集的大小(就樣本和特征而言),而 bootstrap和bootstrap_features控制的是樣本和特征是否是有放回。當使用可用樣本的子集時,可以通過設置 oob_score=True來估計袋外(out-of-bag)樣本的泛化精度。舉一個例子,下面的片段說明了如何實例化KNeighborsClassifier基估計器的bagging集成,每個估計器都建立在50%的樣本和50%的特征的隨機子集上。
>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> bagging = BaggingClassifier(KNeighborsClassifier(),
... max_samples=0.5, max_features=0.5)
| 示例 |
|---|
| 單個估計器 vs bagging:偏差-方差分解 |
參考
[B1999] L. Breiman, “Pasting small votes for classification in large databases and on-line”, Machine Learning, 36(1), 85-103, 1999.
[B1996] L. Breiman, “Bagging predictors”, Machine Learning, 24(2), 123-140, 1996.
[H1998] T. Ho, “The random subspace method for constructing decision forests”, Pattern Analysis and Machine Intelligence, 20(8), 832-844, 1998.
[LG2012] G. Louppe and P. Geurts, “Ensembles on Random Patches”, Machine Learning and Knowledge Discovery in Databases, 346-361, 2012.
1.11.2 由隨機樹組成的森林
sklearn.ensemble集成模塊包括兩種基于隨機決策樹的平均算法:RandomForest算法和Extra-Trees算法。這兩種算法都是專門為樹設計的擾動和組合技術(perturb-and-combine techniques)[B1998] 。這意味著在分類器構造過程中引入隨機性來創建一組不同的分類器的集合。集成之后的預測是每個分類器的平均。
與其他分類器一樣,森林分類器(forest classifiers)必須擬合兩個數組:一個稀疏或密集的X數組, 包含訓練樣本, 形狀是[n_samples, n_features], 還有數組Y, 形狀是 [n_samples], 包含訓練樣本的目標值(類標簽):
>>> from sklearn.ensemble import RandomForestClassifier
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = RandomForestClassifier(n_estimators=10)
>>> clf = clf.fit(X, Y)
和決策樹 decision trees一樣,樹的森林也擴展到多輸出問題 multi-output problems(如果Y是一個形狀為([n_samples, n_outputs])的數組。
1.11.2.1 隨機森林
在隨機森林中(請參閱 RandomForestClassifier和 RandomForestRegressor類), 集成模型中的每棵樹構建時的樣本都是由訓練集經過有放回抽樣(比如a bootstrap sample 自助式采樣法)得來的。
另外,在構建樹的過程中進行結點分割時,選擇的分割點是所有特征的最佳分割點,或特征的大小為 max_features 的隨機子集的最佳分割。(更多細節請看parameter tuning guidelines )。
這兩種隨機的目的是降低森林估計器的方差。事實上,單個決策樹通常表現出很高的方差,并且往往會過擬合。在森林中注入隨機性產生的決策樹具有一定的解耦預測誤差(decoupled prediction errors)。通過取這些預測的平均值,可以抵消掉一些誤差。隨機森林通過組合不同的樹來減少方差,有時以增加一點點偏差為代價。在實踐中,方差減少通常是值得關注的,因此產生了一個整體更好的模型。
與最初的出版物 [B2001]相比,scikit-learn實現通過平均它們的概率預測來組合分類器,而不是讓每個分類器為單個類別進行投票。
1.11.2.2 極端隨機樹
在極端隨機樹(參見 ExtraTreesClassifier 和 ExtraTreesRegressor 類)中,計算分割點方法中的隨機性進一步增強。與隨機森林中一樣,使用了候選特征的隨機子集,但不像隨機森林中是尋找最具區分度的閾值,而是對每個候選特征隨機繪制閾值,并選擇這些隨機生成的閾值中最佳的作為作為分割規則。這種做法通常能夠減少一點模型的方差,代價則是略微地增大偏差:
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import make_blobs
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.tree import DecisionTreeClassifier
>>> X, y = make_blobs(n_samples=10000, n_features=10, centers=100,
... random_state=0)
>>> clf = DecisionTreeClassifier(max_depth=None, min_samples_split=2,
... random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
0.98...
>>> clf = RandomForestClassifier(n_estimators=10, max_depth=None,
... min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
0.999...
>>> clf = ExtraTreesClassifier(n_estimators=10, max_depth=None,
... min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean() > 0.999
True
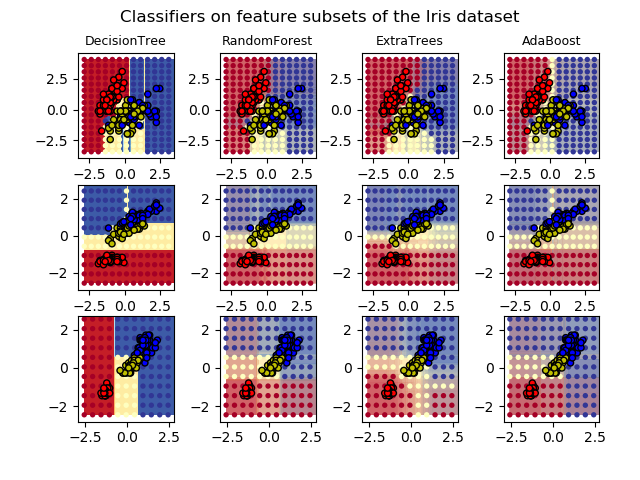
1.11.2.3 參數
使用這些方法時要調整的參數主要是 n_estimators 和 max_features。前者(n_estimators)是森林里樹的數量,通常數量越大,效果越好,但是計算時間也會隨之增加。此外要注意,當樹的數量超過一個臨界值之后,算法的效果并不會很顯著地變好。后者(max_features)是分割節點時考慮的特征的隨機子集的大小。 這個值越低,方差減小得越多,但是偏差的增大也越多。 根據經驗,回歸問題中使用 max_features = None (總是考慮所有的特征而不是一個子集), 分類問題使用 max_features = "sqrt" (隨機考慮 sqrt(n_features) 特征,其中 n_features 是數據中特征的個數)是比較好的默認值。 max_depth = None 和 min_samples_split = 2結合通常會有不錯的效果(即完全生長的樹)。 請記住,這些(默認)值通常不是最佳的,同時還可能消耗大量的內存,最佳參數值應由交叉驗證獲得。 另外,請注意,在隨機森林中,默認使用自助采樣法(bootstrap = True), 然而 extra-trees 的默認策略是使用整個數據集(bootstrap = False)。 當使用自助采樣法方法抽樣時,泛化精度是可以通過剩余的或者袋外(out-of-bag) 的樣本來評估的,設置 oob_score = True 即可實現。
注意:默認參數下模型復雜度是:
O(M*N*log(N)), 其中M是樹的數目,N是樣本數。 可以通過設置以下參數來降低模型復雜度:min_samples_split,?max_leaf_nodes,?max_depth和min_samples_leaf。
1.11.2.4 并行化
最后,這個模塊還支持樹的并行構建和預測結果的并行計算,這可以通過 n_jobs 參數實現。 如果設置 n_jobs = k ,則計算被劃分為 k 個作業,并運行在機器的 k 個核上。 如果設置 n_jobs = -1 ,則使用機器的所有核。 注意由于進程間通信具有一定的開銷,這里的提速并不是線性的(即,使用 k 個作業不會快 k 倍)。 當然,在建立大量的樹,或者構建單個樹需要相當長的時間(例如,在大數據集上)時,(通過并行化)仍然可以實現顯著的加速。
| 示例 |
|---|
| 在iris數據集上繪制決策樹的決策面 基于平行樹的森林的像素重要性 Face completion with a multi-output estimators |
參考
[B2001] Breiman, “Random Forests”, Machine Learning, 45(1), 5-32, 2001.
[B1998] Breiman, “Arcing Classifiers”, Annals of Statistics 1998.
P. Geurts, D. Ernst., and L. Wehenkel, “Extremely randomized trees”, Machine Learning, 63(1), 3-42, 2006.
1.11.2.5 特征重要性評估
特征對目標變量預測的相對重要性可以通過(樹中的決策節點的)特征使用的相對順序(即深度)來進行評估。 決策樹頂部使用的特征對輸入的大部分樣本的最終預測決策做出貢獻;因此,可以使用接受每個特征對最終預測的貢獻的樣本比例來評估該 特征的相對重要性 。scikit-learn通過將特征貢獻的樣本比例與分割時產生的不純度減少相結合, 從而創建了對該特征的預測能力的標準化估計。
通過對多個隨機樹中的 預期貢獻率 (expected activity rates) 取平均,可以減少這種估計的 方差 ,并將其用于特征選擇。這被稱作平均純度減少,或MDI。關于MDI以及隨機森林特征重要性的更多信息,請參考[L2014]。
警告:在基于樹的模型上計算的基于不存度的特征重要性存在兩個缺陷,可能導致誤導性結論。首先,它們是根據從訓練數據集派生出來的統計數據來計算的,因此不一定能告訴我們對于更好的預測保留的數據(held-out dataset), 到底哪些特征才是最重要的。其次,他們傾向于高基數特征,即具有許多不同值的特征。置換特征重要性Permutation feature importance是不受這些缺陷影響的基于不存度計算特征重要性的替代選項。這里兩種方法對獲取特征重要性進行了探討::置換重要性與隨機森林特征重要性(MDI)。
下面的示例顯示了使用 ExtraTreesClassifier 模型對人臉識別任務的單個像素的相對重要性的顏色編碼表示。
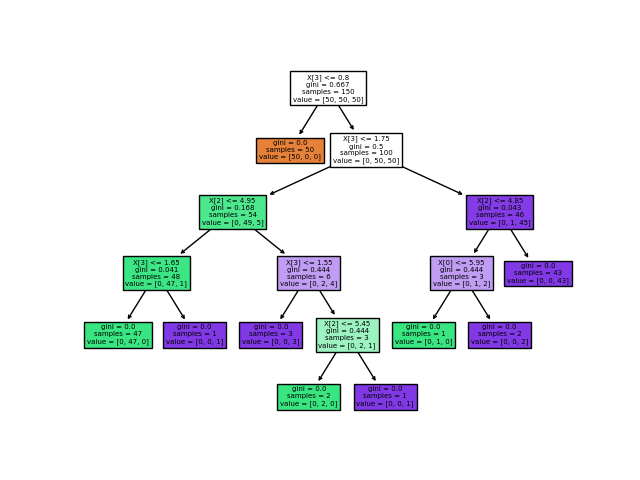 實際上,這些估計值存儲在一個已經擬合的模型的屬性
實際上,這些估計值存儲在一個已經擬合的模型的屬性 feature_importances_上。這是一個大小為(n_features,)的數組,其值為正,總和為1.0。值越高,匹配特征對預測函數的貢獻就越重要。
| 示例 |
|---|
| 基于平行樹的森林的像素重要性 樹森林的特征重要性 |
參考
[L2014] G. Louppe, “Understanding Random Forests: From Theory to Practice”, PhD Thesis, U. of Liege, 2014.
1.11.2.6 完全隨機樹嵌入
RandomTreesEmbedding 實現了一個無監督的數據轉換。 通過由完全隨機樹構成的森林,RandomTreesEmbedding 使用數據最終歸屬的葉子節點的索引值對數據進行編碼。 該索引以 one-of-K 方式編碼,最終形成一個高維的稀疏二值化編碼。 這種編碼可以被非常高效地計算出來,并且可以作為其他學習任務的基礎。 編碼的大小和稀疏度可以通過選擇樹的數量和每棵樹的最大深度來確定。對于集成中的每棵樹的,每個樣本對應其中的一個葉節點。 編碼的大小(維度)最多為 n_estimators * 2 ** max_depth ,即森林中的葉子節點的最大數。
由于相鄰數據點更可能位于一顆樹的同一葉子中,該變換可以作為一種隱式地非參數密度估計。
| 示例 |
|---|
| 基于完全隨機樹的哈希特征變換 手寫數字上的流形學習:局部線性嵌入,Isomap… 比較了手寫體數字的非線性降維技術。 樹集成的特征轉換 比較了基于樹的有監督和無監督特征變換. |
也可以看這里:流形學習技術也可以用來導出特征空間的非線性表示,這些方法也側重于維數約簡。
1.11.3. AdaBoost
sklearn.ensemble 模塊包含了流行的提升算法 AdaBoost, 這個算法是由 Freund 和 Schapire 在 1995 年提出來的[FS1995]。
AdaBoost 的核心思想是用反復調整的數據來訓練一系列的弱學習器(一個弱學習器模型僅僅比隨機猜測好一點, 比如一個簡單的決策樹),由這些弱學習器的預測結果通過加權投票(或加權求和)的方式組合, 產生最終的預測結果。在每一次所謂的提升(boosting)迭代中,數據的修改由應用于每一個訓練樣本的(新) 的權重 組成。 初始化時,將所有弱學習器的權重都設置為 ,因此第一次迭代僅僅是通過原始數據訓練出一個弱學習器。在接下來的連續迭代中,樣本的權重逐個地被修改,學習算法也因此要重新應用這些已經修改的權重的數據。在給定的一個迭代中, 那些在上一輪迭代中被預測為錯誤結果的樣本的權重將會被增加,而那些被預測為正確結果的樣本的權重將會被降低。隨著迭代次數的增加,那些難以預測的樣例的影響將會越來越大,每一個隨后的弱學習器都將會被強迫更加關注那些在之前被錯誤預測的樣例[HTF]。
 AdaBoost可以用于分類和回歸問題:
AdaBoost可以用于分類和回歸問題:
對于多類分類, AdaBoostClassifier實現了AdaBoost-Samme和AdaBoost-SAMME.R[ZRH 2009]。對于回歸, AdaBoostRegressor實現了AdaBoost.R2[D 1997]。
1.11.3.1 使用方法
下面的示例演示如何為100個弱學習器擬合AdaBoost分類器:
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import load_iris
>>> from sklearn.ensemble import AdaBoostClassifier
>>> X, y = load_iris(return_X_y=True)
>>> clf = AdaBoostClassifier(n_estimators=100)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
0.9...
弱學習器的數量由參數n_estimators控制。learning_rate參數控制著弱學習者在最終組合中的貢獻。默認情況下,弱學習器是決策樹。通過 base_estimator 參數可以指定不同的弱學習器。要獲得良好結果的主要參數是n_estimators和基估計器的復雜度(例如,它的深度 max_depth或考慮分裂的最小樣本數min_samples_split)。
| 示例 |
|---|
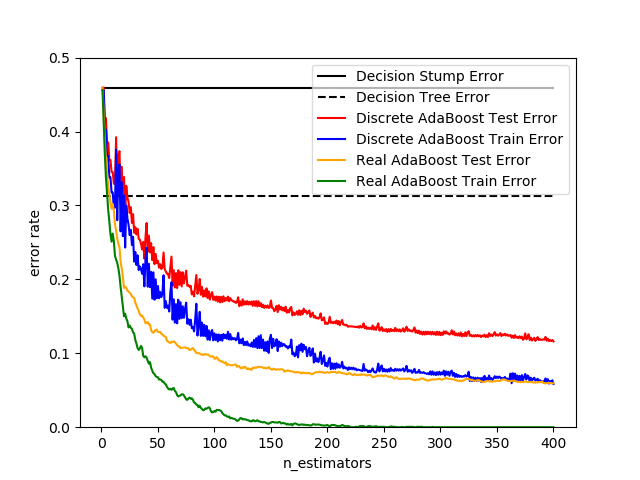
| 離散型與真實型AdaBoost 使用 AdaBoost-SAMME 和 AdaBoost-SAMME.R 比較 decision stump, decision tree(決策樹)和 boosted decision stump(增強決策樹)的分類錯誤 多類AdaBoost決策樹 展示了 AdaBoost-SAMME 和 AdaBoost-SAMME.R 在 multi-class (多類)問題上的性能。 兩類AdaBoost 展示了使用 AdaBoost-SAMME 的非線性可分兩類問題的決策邊界和決策函數值。 基于AdaBoost的決策樹回歸 使用 AdaBoost.R2 算法證明了回歸。 |
參考
[FS1995] Y. Freund, and R. Schapire, “A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting”, 1997. [ZZRH2009] J. Zhu, H. Zou, S. Rosset, T. Hastie. “Multi-class AdaBoost”, 2009. [D1997] Drucker. “Improving Regressors using Boosting Techniques”, 1997. HTF(1,2,3) T. Hastie, R. Tibshirani and J. Friedman, “Elements of Statistical Learning Ed. 2”, Springer, 2009.
1.11.4 梯度樹提升
梯度樹提升Gradient Tree Boosting或梯度提升樹(Gradient Boosted Decision Trees,GBDT)是Booting對任意可微損失函數的推廣。GBDT是一種準確有效的現成程序,可用于各種領域的回歸和分類問題,包括Web搜索、排名和生態領域。
集成模塊 sklearn.ensemble 通過梯度提升樹提供了分類和回歸的方法。
注意:在LightGBM (參看 [LightGBM])的啟發下,Scikit-learn 0.21引入了兩種新的梯度提升樹的實驗實現,即 HistGradientBoostingClassifier和 HistGradientBoostingRegressor。當樣本數大于數萬個樣本時,這些基于直方圖的估計可以比
GradientBoostingClassifier和GradientBoostingRegressor快幾個數量級。他們還內置了對缺失值的支持,從而避免了計算的需要。這些估計器將在下面基于直方圖的梯度提升Histogram-Based Gradient Boosting中更詳細地描述。下面的指南重點介紹
GradientBoostingClassifier和GradientBoostingRegressor,它們可能是小樣本大小的首選,因為在這個設置中,裝箱可能會導致分割點過于接近。
下面介紹了 GradientBoostingClassifier 和 GradientBoostingRegressor的用法和參數。這些估計器最重要的兩個參數是n_estimators和learning_rate。
1.11.4.1 分類
GradientBoostingClassifier 既支持二分類,也支持多類分類。下面的示例說明了如何將梯度提升分類器與100個決策樹作為弱學習者進行匹配:
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.913...
弱學習器的數量(即回歸樹)由參數n_estimators控制,每棵樹的大小The size of each tree可以通過設置樹的深度max_depth來控制,也可以通過通過最大葉節點樹max_leaf_nodes數來控制。學習速率 learning_rate是一個范圍是(0.0,1.0]的一個超參數,它通過shrinkage 來控制過擬合。
注意:超過兩類的分類問題需要在每一次迭代時推導
n_classes個回歸樹。因此,所有的需要推導的樹數量等于n_classes * n_estimators。對于擁有大量類別的數據集我們強烈推薦使用HistGradientBoostingClassifier來代替GradientBoostingClassifier。
1.11.4.2 回歸
對于回歸問題 GradientBoostingRegressor 支持一系列損失函數,這些損失函數可以通過參數 loss 來指定;對于回歸問題默認的損失函數是最小二乘損失( 'ls' )。
>>> import numpy as np
>>> from sklearn.metrics import mean_squared_error
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
>>> X_train, X_test = X[:200], X[200:]
>>> y_train, y_test = y[:200], y[200:]
>>> est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
... max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)
>>> mean_squared_error(y_test, est.predict(X_test))
5.00...
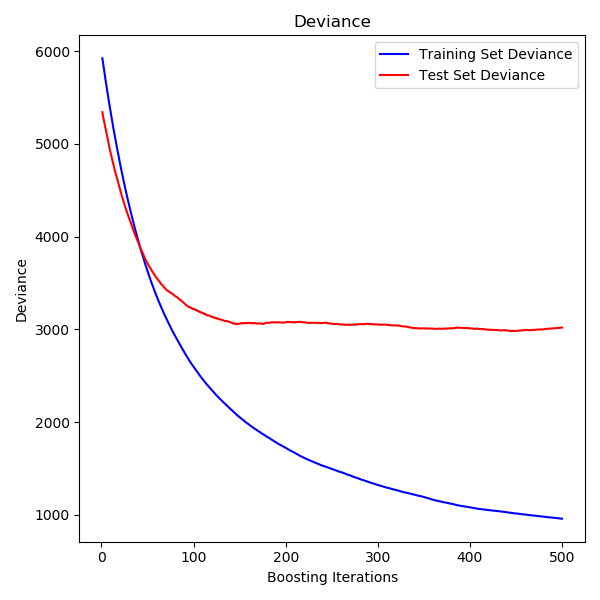
下圖顯示了將最小二乘損失和500個基學習器的GradientBoostingRegressor應用于波士頓房價數據集(sklearn.datasets.load_boston)的結果。左邊的圖顯示了每次迭代時的訓練和測試誤差。每一次迭代時的訓練誤差都存儲在梯度提升模型的train_score_屬性中。每次迭代時的測試誤差可以通過staged_predict方法獲得,該方法返回在每個階段生成預測的生成器。這樣畫圖可以通過早期停止來確定樹的最優數目(即 n_estimators)。右邊的圖顯示了基于不存度的特征重要性,它可以通過feature_importances_屬性獲得。
| 示例 |
|---|
| 梯度提升回歸 梯度提升袋外估計 |
1.11.4.3 訓練額外的弱學習器
GradientBoostingRegressor 和 GradientBoostingClassifier都支持 warm_start=True ,這允許您在已經擬合的模型中添加更多的估計器
>>> _ = est.set_params(n_estimators=200, warm_start=True)
# set warm_start and new nr of trees
>>> _ = est.fit(X_train, y_train) # fit additional 100 trees to est
>>> mean_squared_error(y_test, est.predict(X_test))
3.84...
1.11.4.4 控制樹的大小
回歸樹基學習器的大小定義了梯度提升模型可以捕捉到的變量交互的水平。一般來說,深度h的樹可以捕捉h階的相互作用。有兩種方法可以控制單個回歸樹的大小。
如果你指定 max_depth=h ,那么將會產生一個深度為 h 的完全二叉樹。這棵樹將會有(至多) 2**h 個葉子節點和 2**h - 1 個分割節點。
或者,您還可以通過參數max_leaf_nodes指定葉節點的數目來控制樹的大小。在這種情況下,樹將使用最佳優先搜索來生長,這種搜索方式是通過每次選取對不純度提升最大的節點來首先展開。一棵 max_leaf_nodes=k 的樹擁有 k - 1 個切分節點,因此可以模擬max_leaf_nodes - 1階的交互作用。
我們發現 max_leaf_nodes=k 可以給出與 max_depth=k-1 品質相當的結果,但是其訓練速度明顯更快,同時也會以多一點的訓練誤差作為代價。參數 max_leaf_nodes 對應于文章 [F2001]中梯度提升章節中的變量 J ,同時與 R 語言的 gbm 包的參數 interaction.depth 相關,兩者間的關系是 max_leaf_nodes == interaction.depth + 1 。
1.11.4.5 數學公式
我們首先說GBRT的回歸,然后詳細介紹分類案例。
1.11.4.5.1 回歸
GBRT回歸器是一種加法模型,其對給定輸入的預測由以下形式給出:
其中,是在boosting中被稱為弱學習器的估計器。梯度樹提升采用固定大小的決策樹回歸器作為弱學習器。常數對應n_estimators參數。
與其他提升算法類似,GBRT是以貪婪的方式構建的:
其中新添加的樹中的是為了最小化損失的總和而擬合的,給定前面的集成器為:
其中由loss參數定義,詳見下一節。
默認情況下,初始模型選擇使損失最小化的常數:對于最小二乘損失,這是目標值的經驗平均值。初始模型也可以通過init參數指定。
使用一階泰勒(Taylor)近似,的值可以近似為如下:
注意:簡要地說, 一階泰勒近似是:, 這里對應, 對應。
是損失相對于第二個參數的導數, 這里按計算。對于任何給定的,由于損失都是可微的,因此很容易計算出它的閉合形式。我們用表示。
除去常數項,我們有:
如果被擬合來預測的值與負梯度成正比,則這是最小化的。因此,在每次迭代時,被擬合的估計器用來預測樣本的負梯度。梯度在每次迭代中都會被更新。這可以看作是函數空間中的某種梯度下降。
注意:注意,對于一些損失,例如最小絕對偏差(LAD),其梯度為±1,擬合的預測的值不夠精確:這樣樹只能輸出整數值。因此,一旦樹被擬合,樹的葉子上的值就會被修改,使葉子上的能能最小化損失。更新是依賴于損失的:對于LAD損失,葉子的值將被更新為該葉中樣本的中值。
1.11.4.5.2 分類
梯度提升的分類非常類似于回歸的情況。然而,樹的總和 與預測不是同質的:它不能是一個類,因為樹預測的是連續值。
從到類或概率的映射依賴于損失。對于偏差(或對數損失), 屬于正類的概率被建模為,其中是sigmoid函數。
對于多類分類,K樹(對于K類)是在每一個迭代中構建的。屬于k類的概率被建模為值的一個Softmax。
請注意,即使對于分類任務,基估計器仍然是一個回歸器,而不是分類器。這是因為基估計器被訓練來預測(負)梯度,這些梯度總是連續的。
1.11.4.6 損失函數
支持下面這些損失函數,并可以使用參數 loss指定這些函數:
回歸 最小二乘( 'ls'):回歸的自然選擇,因為它具有優越的計算特性。用目標值的平均值給出了初始模型。最小絕對偏差( 'lad'):一個穩健的回歸損失函數。初始模型由目標值的中值給出。Huber( ‘Huber’):另一個結合最小二乘和最小絕對偏差的穩健損失函數;使用alpha控制異常值的靈敏度(詳見[F2001])。Quantile ( 'quantile'):分位數回歸的損失函數。使用0 < alpha < 1指定分位數。此損失函數可用于創建預測間隔 (參見梯度提升回歸的預測間隔 Prediction Intervals for Gradient Boosting Regression)
分類 二項偏差( 'deviance'):二分類的負二項式對數似然損失函數(提供概率估計)。用對數比率給出了初始模型。多項偏差( 'deviance'):對于多分類問題的負的多項對數似然損失函數具有n_classes個互斥的類。提供概率估計。 初始模型由每個類的先驗概率給出.在每一次迭代中n_classes回歸樹被構建,這使得 GBRT 在處理多類別數據集時相當低效。指數損失( 'exponential'):與AdaBoostClassifier具有相同的損失函數。與'deviance'相比,對被錯誤標記的樣本的魯棒性較差,僅用于在二分類問題。
1.11.4.7 學習收縮率
[F2001] 提出了一種簡單的正則化策略,通過常數因子 來衡量每個弱學習器的貢獻:
參數也稱為學習速率,因為它可以縮放步長、梯度下降過程;它可以通過 learning_rate參數來設置。
參數learning_rate與 n_estimators(弱學習器的個數)有很強的相互作用。較小的learning_rate值要求較多的弱學習者以保持一個恒定的訓練誤差。經驗證據表明,較小的learning_rate有利于更好的測試誤差。[HTF]建議將學習速率設置為一個小常數(例如,learning_rate <= 0.1),并通過早期的停止選擇n_estimators。關于learning_rate 和 n_estimators 之間相互作用的更詳細的討論,見 [R2007]。
1.11.4.8 子采樣(Subsampling)
[F1999] 提出了隨機梯度提升,這種方法將梯度提升(gradient boosting)和 bootstrap averaging(bagging) 相結合。在每次迭代中,基分類器是通過抽取所有可利用訓練集中一小部分的 subsample 訓練得到的子樣本采用無放回的方式采樣。 subsample 參數的值一般設置為 0.5 。
下圖表明了收縮與否和子采樣對于模型擬合好壞的影響。我們可以明顯看到指定收縮率比沒有收縮擁有更好的表現。而將子采樣和收縮率相結合能進一步的提高模型的準確率。相反,使用子采樣而不使用收縮的結果十分糟糕。
 另一種降低方差的策略是對隨機森林分類器中類似隨機分裂的特征進行二次采樣。通過
另一種降低方差的策略是對隨機森林分類器中類似隨機分裂的特征進行二次采樣。通過max_features參數可以控制子采樣特征的數量。
注意:使用一個較小的
max_Feature值可以顯著減少運行時。
隨機梯度提升允許計算測試偏差的袋外估計(Out-of-bag),方法是計算那些不在自助采樣之內的樣本(比如袋外數據)偏差的改進。這些改進存儲在屬性oob_improvement_中。如果將第階段添加到當前的預測中,則 oob_improvement_[i]保存了在OOB樣本損失方面的改進。袋外估計可以使用在模型選擇中,例如決定最優迭代次數。 OOB 估計通常都很悲觀,因此我們推薦使用交叉驗證來代替它,而當交叉驗證太耗時時我們就只能使用 OOB 了。
| 例子 |
|---|
| 梯度提升正則 梯度提升袋外估計 隨機森林的OOB |
1.11.4.9 特征重要性的解釋
通過簡單的可視化樹結構,可以很容易地解釋單個決策樹。然而,梯度提升模型包含了數百棵回歸樹,因此它們很難通過對單個樹的可視化來進行解釋。幸運的是,已經提出了一些技術來總結和解釋梯度提升模型。
通常,特性對預測目標響應的貢獻并不相同;在許多情況下,大多數特征實際上是無關的。在解釋模型時,第一個問題通常是:重要的特征是什么,并且它們在預測目標響應方面有何貢獻?
單個決策樹本質上通過選擇合適的分割點來進行特征選擇。這些信息可以用來度量每個特征的重要性;基本思想是:在樹的分割點中使用某特征越頻繁,該特性就越重要。這種重要性的概念可以通過簡單地平均每個樹的基于不存度的特征重要性來擴展到決策樹集成器上(更多細節請參見特征重要性評估Feature importance evaluation)。
一個擬合的梯度提升模型的特征重要性分數可以通過feature_importances_屬性訪問:
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> clf.feature_importances_
array([0.10..., 0.10..., 0.11..., ...
請注意,這種特征重要性的計算是基于熵的,并且它不同于sklearn.inspection.permutation_importance,后者是基于特征的排列。
| 示例 |
|---|
| 梯度提升回歸 |
1.11.5 基于直方圖的梯度提升
Scikit-Leard0.21介紹了兩種新的梯度提升樹的實驗實現,即基于LightGBM(見[LightGBM])的HistGradientBoostingClassifier 和 HistGradientBoostingRegressor。
當樣本數大于數萬個樣本時,這些基于直方圖的估計器可以比 GradientBoostingClassifier 和GradientBoostingRegressor 快幾個數量級。
他們還內置了對缺失值的支持,從而避免了計算機的需要。
這些快速估計器首先將輸入樣本X放入整數值箱(通常為256個),這極大地減少了要考慮的分裂點數,并允許算法在構建樹時利用基于整數的數據結構(直方圖)而不是依賴排序的連續值。這些估計器的API略有不同,對一些損失函數的 GradientBoostingClassifier 和 GradientBoostingRegressor的實例將不再支持一些特性。
這些估計器仍然是實驗性的:它們的預測和API可能在沒有任何反對周期的情況下發生變化。要使用它們,您需要顯式地導入enable_hist_gradient_boosting:
>>> # explicitly require this experimental feature
>>> from sklearn.experimental import enable_hist_gradient_boosting # noqa
>>> # now you can import normally from ensemble
>>> from sklearn.ensemble import HistGradientBoostingClassifier
| 示例 |
|---|
| 部分依賴圖 |
1.11.5.1 使用方法
大多數參數來自 GradientBoostingClassifier 和GradientBoostingRegressor。一個例外是max_iter參數,該參數取代 n_estimators,并控制提升過程的迭代次數:
>>> from sklearn.experimental import enable_hist_gradient_boosting
>>> from sklearn.ensemble import HistGradientBoostingClassifier
>>> from sklearn.datasets import make_hastie_10_2
>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]
>>> clf = HistGradientBoostingClassifier(max_iter=100).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.8965
可用的回歸損失有‘least_squares’, ‘least_absolute_deviation’(對異常值不太敏感)和 ‘poisson’(非常適合模型計數和頻率)。在分類方面,‘binary_crossentropy’ 用于二分類, ‘categorical_crossentropy’用于多分類。默認情況下,損失函數是 ‘auto’,并將更具傳入的y選擇合適的損失函數進行fit。
樹的大小可以通過 max_leaf_nodes, max_depth, 和 min_samples_leaf 參數來控制。
用于存儲數據的回收箱數量由max_bins參數控制。使用較少的垃圾箱作為一種形式的正規化。通常建議使用盡可能多的回收箱,這是默認的。
用于裝數據的箱子數量由max_bins參數控制。使用較少的箱子可以作為一種正則化的形式。通常建議使用盡可能多的箱子,這是默認的。
l2_regularization參數是損失函數上的正則化參數,對應于[XGBoost]方程(2)中的。
注意,如果樣本數大于10,000,則默認啟用早期停止。早期停止行為通過 early-stopping, scoring, validation_fraction, n_iter_no_change, and tol參數來控制.使用一個隨意的scorer,或僅僅是訓練或驗證的損失是有可能早期停止的。注意,由于技術原因,使用 scorer比使用損失要慢得多。默認情況下,如果訓練集中至少有10,000個樣本,則使用驗證損失執行早期停止。
1.11.5.2 缺失值支持
HistGradientBoostingClassifier 和 HistGradientBoostingRegressor內建了缺失值支持。
在訓練過程中,生長的樹根據潛在的增益,在每次分割時無論樣本是否含有缺失值都應該被劃分到右邊或者左邊。因此,因此, 在預測時,有缺失值的樣本也會被分配給左或右的子節點:
>>> from sklearn.experimental import enable_hist_gradient_boosting # noqa
>>> from sklearn.ensemble import HistGradientBoostingClassifier
>>> import numpy as np
>>> X = np.array([0, 1, 2, np.nan]).reshape(-1, 1)
>>> y = [0, 0, 1, 1]
>>> gbdt = HistGradientBoostingClassifier(min_samples_leaf=1).fit(X, y)
>>> gbdt.predict(X)
array([0, 0, 1, 1])
當缺失模式具有預測性時,可以根據特征值是否缺失進行分割:
>>> X = np.array([0, np.nan, 1, 2, np.nan]).reshape(-1, 1)
>>> y = [0, 1, 0, 0, 1]
>>> gbdt = HistGradientBoostingClassifier(min_samples_leaf=1,
... max_depth=2,
... learning_rate=1,
... max_iter=1).fit(X, y)
>>> gbdt.predict(X)
array([0, 1, 0, 0, 1])
如果在訓練期間給定特征下沒有碰見缺失值,則會將有缺少值的樣本映射到具有最多樣本的那個子節點上。
1.11.5.3 樣本加權支持
HistGradientBoostingClassifier 和 HistGradientBoostingRegressor 在fit的時候可以對樣本進行加權。
下面的小示例演示了模型如何忽略樣本權重為零的樣本:
>>> X = [[1, 0],
... [1, 0],
... [1, 0],
... [0, 1]]
>>> y = [0, 0, 1, 0]
>>> # ignore the first 2 training samples by setting their weight to 0
>>> sample_weight = [0, 0, 1, 1]
>>> gb = HistGradientBoostingClassifier(min_samples_leaf=1)
>>> gb.fit(X, y, sample_weight=sample_weight)
HistGradientBoostingClassifier(...)
>>> gb.predict([[1, 0]])
array([1])
>>> gb.predict_proba([[1, 0]])[0, 1]
0.99...
正如您所看到的,[1, 0]被輕松地歸為1,因為前兩個樣本由于其樣本權重而被忽略。
實現細節:考慮樣本權重等于將梯度(和Hessians)乘以樣本權重。注意,二進制階段(特別是分位數計算)沒有考慮權重。
1.11.5.4 單調約束
根據手頭的問題,您可能事先了解到,給定的特征通常會對目標值產生積極(或負面)影響。例如,在其他條件相同的情況下,較高的信用評分應該會增加獲得貸款批準的可能性。單調約束允許您將這些先驗知識集成到模型中。
正單調約束是形式的約束:
, 其中是具有兩個特征的預測器。
同樣,負單調約束的形式如下:
請注意,單調約束只約束輸出“所有其他條件相同”。事實上,下列關系并不是通過積極的約束而得到加強的:
您可以使用 monotonic_cst參數為每個特征指定一個單調約束。對于每個特征,值0表示沒有約束,而-1和1分別表示負約束和正約束:
>>> from sklearn.experimental import enable_hist_gradient_boosting # noqa
>>> from sklearn.ensemble import HistGradientBoostingRegressor
... # positive, negative, and no constraint on the 3 features
>>> gbdt = HistGradientBoostingRegressor(monotonic_cst=[1, -1, 0])
在二分類中,施加單調約束意味著特征對屬于正類的概率有正/負的影響。對于多類分類,不支持單調約束。
| 示例 |
|---|
| 單調約束 |
1.11.5.5 低級并行
HistGradientBoostingClassifier and HistGradientBoostingRegressor通過Cython使用使用OpenMP并行化。有關如何控制線程數量的詳細信息,請參閱我們的 Parallelism說明。
以下部分并行化:
將樣本從真實值映射到整數值箱(然而,找到bin閾值是連續的) 構建直方圖在特征上并行化 在節點上找到最佳分割點的方法是在特征上并行化 在fit期間,將樣本映射到左、右兩個子節點,并在樣本上并行化 梯度和Hessians計算在樣本上并行化 預測在樣本上并行化
1.11.5.6 為什么它更快
梯度提升過程的瓶頸是決策樹的建立。構建一個傳統的決策樹(如在其他GBDTs、GradientBoostingClassifier 和 GradientBoostingRegressor中)需要在每個節點(針對每個特征)對樣本進行排序。排序是必要的,以便能夠有效地計算一個分裂點的潛在增益。因此,分割單個節點的復雜度為,其中是節點上的樣本數。
相反,HistGradientBoostingClassifier 和 HistGradientBoostingRegressor不需要對特征值進行排序,而是使用名為histogram的數據結構,其中樣本是隱式排序的。構造histogram的復雜度為,因此節點分裂過程的復雜度為,遠遠小于以前的算法。另外,我們不考慮個分裂點,而是只考慮max_bins分裂點,它要小得多。
為了建立histograms,輸入數據X需要被綁定到整數值的箱子中。這個裝箱過程確實需要對特征值進行排序,但它只在提升過程開始時發生一次(而不是在每個節點,不像GradientBoostingClassifier 和 GradientBoostingRegressor。
最后,HistGradientBoostingClassifier 和 HistGradientBoostingRegressor的實現了許多并行化。
參考
[F1999] Friedmann, Jerome H., 2007, “Stochastic Gradient Boosting”
[R2007] G. Ridgeway, “Generalized Boosted Models: A guide to the gbm package”, 2007
[XGBoost] Tianqi Chen, Carlos Guestrin, “XGBoost: A Scalable Tree Boosting System”
LightGBM(1,2) Ke et. al. “LightGBM: A Highly Efficient Gradient BoostingDecision Tree”
1.11.6 投票分類器
VotingClassifier (投票分類器)的原理是結合了多個不同的機器學習分類器,并且采用多數表決(majority vote)(硬投票) 或者平均預測概率(軟投票)的方式來預測分類標簽。 這樣的分類器可以用于一組同樣表現良好的模型,以便平衡它們各自的弱點。
1.11.6.1 多數類標簽(多數/硬投票)
在多數投票中,對于每個特定樣本的預測類別標簽是所有單獨分類器預測的類別標簽中票數占據多數(模式)的類別標簽。
例如,如果給定樣本的預測是
classifier 1 -> class 1 classifier 2 -> class 1 classifier 3 -> class 2
VotingClassifier( voting='hard')將根據多數類標簽將示例分類為 “class 1”。
在平局的情況下, VotingClassifier將根據升序排序順序選擇類。例如,在下面的場景中
classifier 1 -> class 2 classifier 2 -> class 1
這種情況下, class 1 將會被指定為該樣本的類標簽。
1.11.6.2 使用方法
下面的示例演示如何擬合多數規則分類器:
>>> from sklearn import datasets
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import VotingClassifier
>>> iris = datasets.load_iris()
>>> X, y = iris.data[:, 1:3], iris.target
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(n_estimators=50, random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(
... estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
... voting='hard')
>>> for clf, label in zip([clf1, clf2, clf3, eclf], ['Logistic Regression', 'Random Forest', 'naive Bayes', 'Ensemble']):
... scores = cross_val_score(clf, X, y, scoring='accuracy', cv=5)
... print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
Accuracy: 0.95 (+/- 0.04) [Logistic Regression]
Accuracy: 0.94 (+/- 0.04) [Random Forest]
Accuracy: 0.91 (+/- 0.04) [naive Bayes]
Accuracy: 0.95 (+/- 0.04) [Ensemble]
1.11.6.3 加權平均概率(軟投票)
與多數投票(硬投票)相比,軟投票將類別標簽返回為預測概率之和的 argmax 。
通過weights參數,可以為每個分類器分配特定的權重。當提供權值時,收集每個分類器的預測類概率,乘以分類器權重,然后進行平均。然后將具有最高平均概率的類別標簽確定為最終類別標簽。
為了用一個簡單的例子來說明這一點,讓我們假設我們有3個分類器和一個3類分類問題,其中我們為所有分類器分配相等的權重:w1=1, w2=1, w3=1。
然后計算樣本的加權平均概率如下:
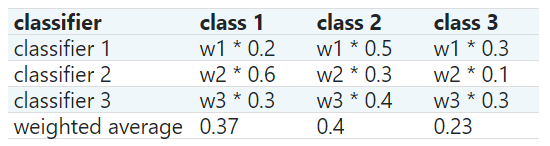 這里,預測的類標簽是2,因為它具有最高的平均概率。
這里,預測的類標簽是2,因為它具有最高的平均概率。
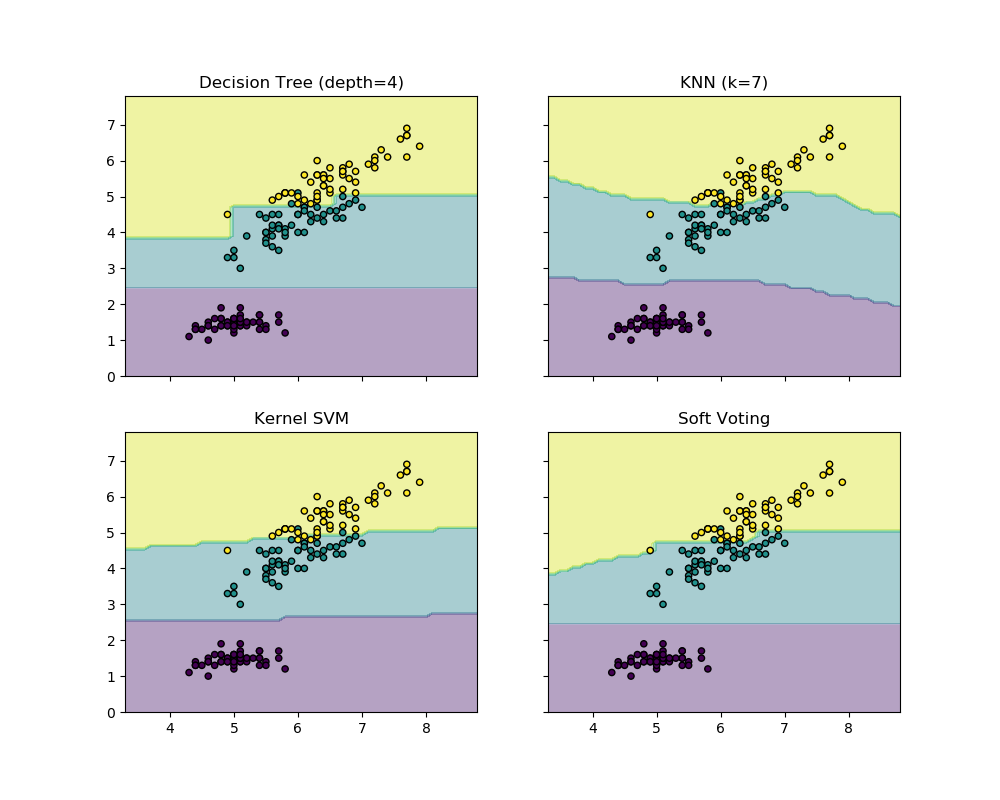
下面的示例說明了在基于線性支持向量機、決策樹和K-最近鄰分類器的基礎上使用軟 VotingClassifier 時,決策區域可能如何變化:
>>> from sklearn import datasets
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> from sklearn.svm import SVC
>>> from itertools import product
>>> from sklearn.ensemble import VotingClassifier
>>> # Loading some example data
>>> iris = datasets.load_iris()
>>> X = iris.data[:, [0, 2]]
>>> y = iris.target
>>> # Training classifiers
>>> clf1 = DecisionTreeClassifier(max_depth=4)
>>> clf2 = KNeighborsClassifier(n_neighbors=7)
>>> clf3 = SVC(kernel='rbf', probability=True)
>>> eclf = VotingClassifier(estimators=[('dt', clf1), ('knn', clf2), ('svc', clf3)],
... voting='soft', weights=[2, 1, 2])
>>> clf1 = clf1.fit(X, y)
>>> clf2 = clf2.fit(X, y)
>>> clf3 = clf3.fit(X, y)
>>> eclf = eclf.fit(X, y)
1.11.6.4 投票分類器(VotingClassifier)在網格搜索(GridSearchCV)的應用
VotingClassifier還可以與 GridSearchCV一起使用,以調整單個估計器的超參數:
>>> from sklearn.model_selection import GridSearchCV
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(
... estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
... voting='soft'
... )
>>> params = {'lr__C': [1.0, 100.0], 'rf__n_estimators': [20, 200]}
>>> grid = GridSearchCV(estimator=eclf, param_grid=params, cv=5)
>>> grid = grid.fit(iris.data, iris.target)
1.11.6.5 使用方法
為了通過預測的類別概率來預測類別標簽(投票分類器中的 scikit-learn estimators 必須支持 predict_proba方法):
>>> eclf = VotingClassifier(
... estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
... voting='soft'
... )
可選地,可以為各個分類器提供權重:
>>> eclf = VotingClassifier(
... estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
... voting='soft', weights=[2,5,1]
... )
1.11.7 投票回歸器
VotingRegressor的思想是將上不同的機器學習回歸器組合起來,并返回平均預測值。這樣的回歸器對于一組同樣表現良好的模型是有用的,以平衡它們各自的弱點。
1.11.7.1 使用方法
下面的示例演示如何擬合VotingRegressor:
>>> from sklearn.datasets import load_boston
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.ensemble import RandomForestRegressor
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.ensemble import VotingRegressor
>>> # Loading some example data
>>> X, y = load_boston(return_X_y=True)
>>> # Training classifiers
>>> reg1 = GradientBoostingRegressor(random_state=1, n_estimators=10)
>>> reg2 = RandomForestRegressor(random_state=1, n_estimators=10)
>>> reg3 = LinearRegression()
>>> ereg = VotingRegressor(estimators=[('gb', reg1), ('rf', reg2), ('lr', reg3)])
>>> ereg = ereg.fit(X, y)
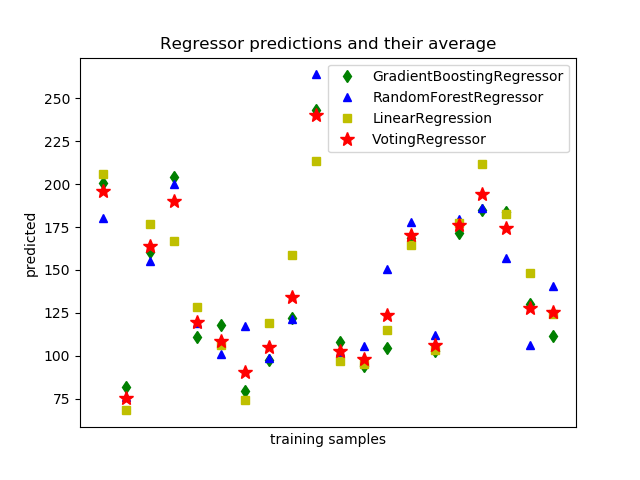
| 示例 |
|---|
| 繪制單獨與投票回歸預測 |
1.11.8 疊加泛化
疊加泛化是一種組合估計器減少偏差的方法 [W1992] [HTF]。更準確地說,每一個估計器的預測被堆疊在一起,并作為最終估計器的輸入來計算預測。這個最終的估計器是通過交叉驗證來訓練的。
StackingClassifier and StackingRegressor 提供了適用于分類和回歸問題的策略。
estimators對應于在估計器的列表, 它們在輸入數據上并行地堆疊在一起。它應該是給出名字和估計器的列表:
>>> from sklearn.linear_model import RidgeCV, LassoCV
>>> from sklearn.svm import SVR
>>> estimators = [('ridge', RidgeCV()),
... ('lasso', LassoCV(random_state=42)),
... ('svr', SVR(C=1, gamma=1e-6))]
final_estimator將使用 estimators的預測作為輸入。當使用StackingClassifier 或者StackingRegressor, 時,它需要是一個分類器或回歸器:
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.ensemble import StackingRegressor
>>> reg = StackingRegressor(
... estimators=estimators,
... final_estimator=GradientBoostingRegressor(random_state=42))
為了訓練estimators和final_estimator,需要對訓練數據調用fit方法:
>>> from sklearn.datasets import load_boston
>>> X, y = load_boston(return_X_y=True)
>>> from sklearn.model_selection import train_test_split
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... random_state=42)
>>> reg.fit(X_train, y_train)
StackingRegressor(...)
在訓練過程中,estimators對整個訓練數據X_train進行擬合。它們將在調用 predict或“預測 predict_proba時被調用。為了推廣和避免過擬合,final_estimator在out-samples上被訓練, 內部使用 sklearn.model_selection.cross_val_predict。
對于 StackingClassifier,請注意, estimators的輸出由參數stack_method控制,并由每個估計器調用。該參數要么是字符串,即估計器方法名稱,要么是'auto',它將根據可用性自動識別可用的方法,并按偏好順序進行測試:predict_proba, decision_function and predict。
StackingRegressor and StackingClassifier可以用作任何其他的回歸者或分類器,通用方法predict, predict_proba, 和 decision_function ,例如:
>>> y_pred = reg.predict(X_test)
>>> from sklearn.metrics import r2_score
>>> print('R2 score: {:.2f}'.format(r2_score(y_test, y_pred)))
R2 score: 0.81
請注意,還可以使用 transform方法獲得堆疊 estimators的輸出:
>>> reg.transform(X_test[:5])
array([[28.78..., 28.43... , 22.62...],
[35.96..., 32.58..., 23.68...],
[14.97..., 14.05..., 16.45...],
[25.19..., 25.54..., 22.92...],
[18.93..., 19.26..., 17.03... ]])
在實際應用中,堆疊預測器預測的效果與基本層的最佳預測器一樣好,有時甚至通過將這些預測器的不同強度組合在一起而優于這些預測器。然而,訓練堆疊預測器在計算上是昂貴的。
注意:
StackingClassifier,當使用stack_method_='predict_proba'時,當問題是二分類問題時,將刪除第一列。實際上,每個估計器預測的兩個概率列都是完全共線的。
注意:可以通過向
StackingClassifier或者StackingRegressor分配final_estimator來實現多個堆疊層:>>> final_layer = StackingRegressor(
... estimators=[('rf', RandomForestRegressor(random_state=42)),
... ('gbrt', GradientBoostingRegressor(random_state=42))],
... final_estimator=RidgeCV()
... )
>>> multi_layer_regressor = StackingRegressor(
... estimators=[('ridge', RidgeCV()),
... ('lasso', LassoCV(random_state=42)),
... ('svr', SVR(C=1, gamma=1e-6, kernel='rbf'))],
... final_estimator=final_layer
... )
>>> multi_layer_regressor.fit(X_train, y_train)
StackingRegressor(...)
>>> print('R2 score: {:.2f}'
... .format(multi_layer_regressor.score(X_test, y_test)))
R2 score: 0.83
參考:
[W1992] Wolpert, David H. “Stacked generalization.” Neural networks 5.2 (1992): 241-259.
