2.2. 流形學習?

? Look for the bare necessities

? The simple bare necessities

? Forget about your worries and your strife

? I mean the bare necessities

? Old Mother Nature’s recipes

? That bring the bare necessities of life

? – Baloo’s song [The Jungle Book]

流形學習是一種非線性降維方法。這一任務的算法基于這樣的思想:許多數據集的維數過高是人為的。

2.2.1. 介紹

高維數據集很難可視化。雖然可以繪制二維或三維數據來顯示數據的固有結構，但是等價的高維圖就不那么直觀了。為了改善可視化數據集的結構，必須以某種方式減少維數。

完成這種降維最簡單的方法是對數據進行隨機投影。雖然這允許在一定程度上可視化數據結構，但是選擇隨機性的方式還有很多需要改進的地方。在隨機投影中，數據中更有趣的結構可能會丟失。

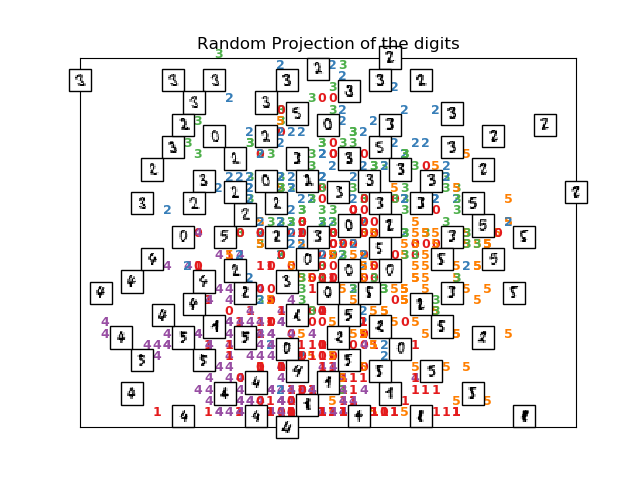
為了解決這個問題，設計了一些有監督和無監督的線性降維框架，如主成分分析(PCA)、獨立成分分析、線性判別分析等。這些算法定義了特定的規則來選擇數據的“有趣的”線性投影。這些方法可能非常強大，但是常常會忽略數據中重要的非線性結構。

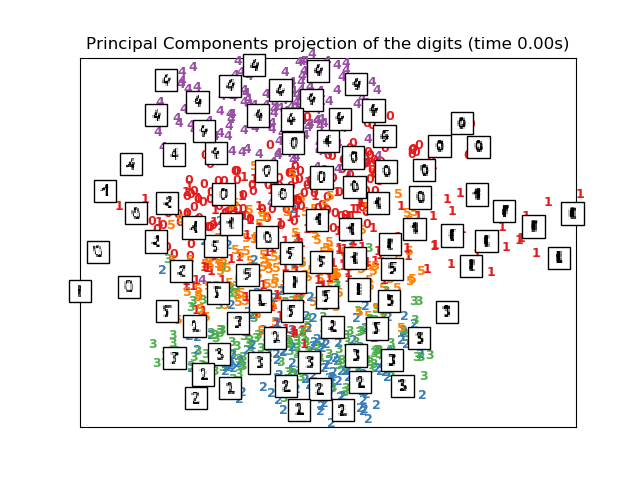
流形學習可以被認為是一種把線性框架（如主成分分析）推廣到數據中敏感的非線性結構的嘗試。雖然有監督變量存在，但典型的流形學習問題是無監督的:它從數據本身學習數據的高維結構，而不使用預先確定的分類。

示例：

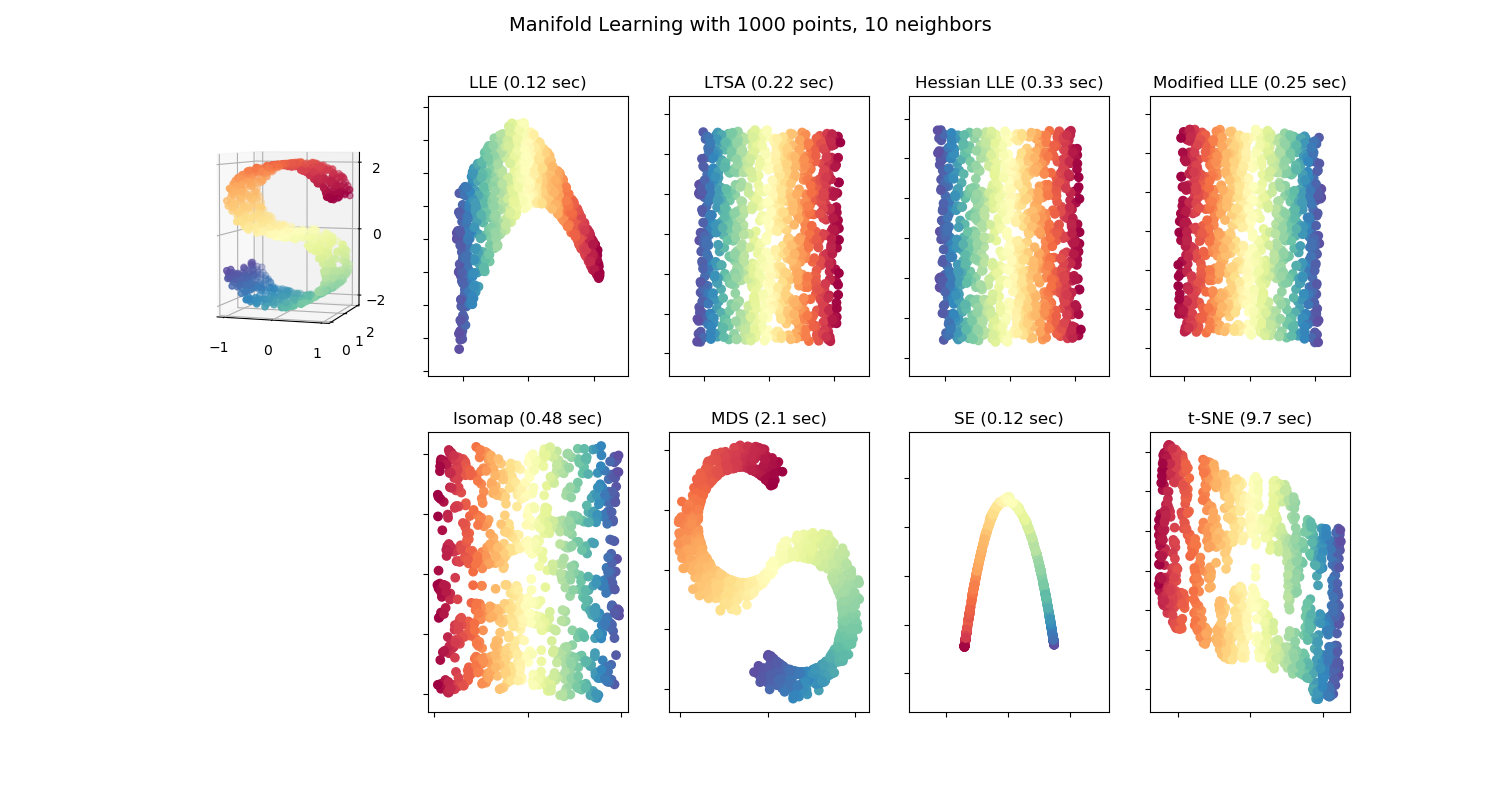
參見手寫數字上的流形學習：局部線性嵌入，Isomap… ,手寫數字降維的示例。
參見流形學習方法的比較 ,有關玩具 “S-曲線” 數據集降維的示例。

scikit-learn中提供的多種學習實現總結如下

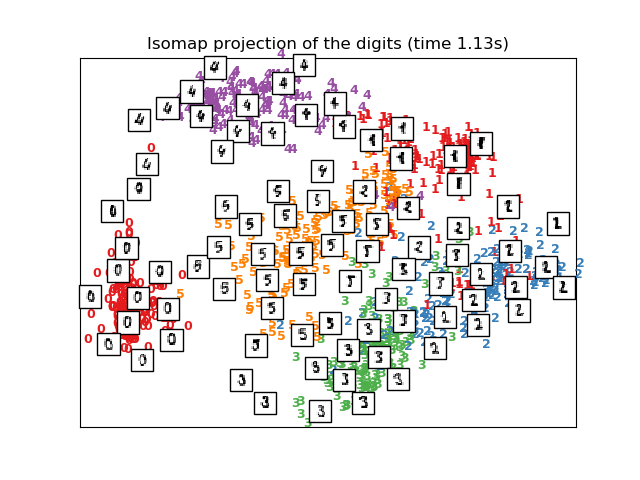
2.2.2. Isomap

Isomap算法是最早的流形學習方法之一，它是等距映射的縮寫。Isomap可以看作是多維尺度分析(MDS)或核主成分分析的擴展。Isomap尋求一種更低維度的嵌入，以保持所有點之間的測地線距離（geodesic distances）。Isomap可以通過Isomap 對象來執行。

2.2.2.1. 復雜度

Isomap 算法包括三個階段:

**最近鄰搜索.**Isomap使用 sklearn.neighbors.BallTree 高效的進行近鄰搜索。對于維度中個點的個最近鄰，其代價近似為。
最短路徑圖搜索. 這方面算法中已知最有效的算法是 Dijkstra 算法或 Floyd-Warshall 算法，復雜度分別是約和。用戶可通過使用 isomap 的 path_method 關鍵字來選擇算法。如果未指定，代碼會嘗試為輸入數據選擇最佳算法。
**部分特征值分解.**嵌入編碼在對應的xisomap核的個最大特征值的特征向量中。對于一個密集求解器，代價大約是。這個代價通常可以通過ARPACK求解器來提高。用戶可以使用Isomap的path_method關鍵字指定特征求解器。如果未指定，代碼將嘗試為輸入數據選擇最佳算法。

Isomap的總體復雜度是

: 訓練數據點個數
: 輸入維度
: 最近鄰個數
: 輸出維度

參考資料:

“A global geometric framework for nonlinear dimensionality reduction” Tenenbaum, J.B.; De Silva, V.; & Langford, J.C. Science 290 (5500)

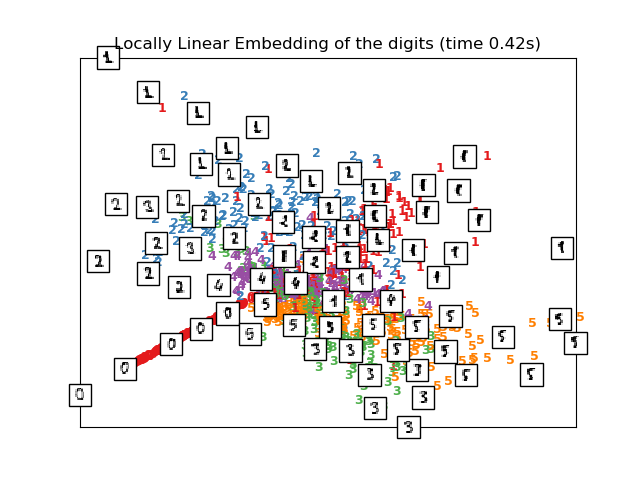
2.2.3. 局部線性嵌入

局部線性嵌入（LLE）通過保留局部鄰域內的距離來尋求數據的低維投影。它可以被認為是一系列的局部主成分分析在全局范圍內的相互比較，找到最優的局部非線性嵌入。

局部線性嵌入可以通過 locally_linear_embedding 函數或其面向對象的等效方法 LocallyLinearEmbedding 來實現。

2.2.3.1. 復雜度

標準的 LLE 算法包括三個階段:

最鄰近搜索. 參見上述 Isomap 討論。
構造權重矩陣. , LLE 權重矩陣的構造包括每個局部鄰域的線性方程的解。
部分特征值分解. 參見上述 Isomap 討論。

標準 LLE 的整體復雜度是

: 訓練數據點個數

: 輸入維度

: 最近鄰個數

: 輸出維度

參考資料:

“Nonlinear dimensionality reduction by locally linear embedding” Roweis, S. & Saul, L. Science 290:2323 (2000)

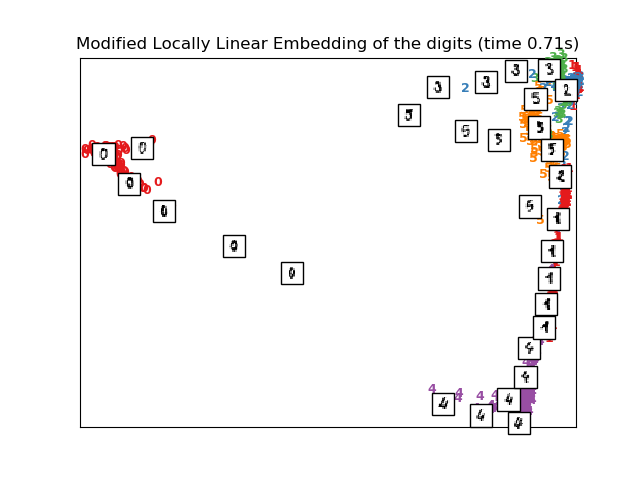
2.2.4. 改進型局部線性嵌入（MLLE）

局部線性嵌入(LLE)一個眾所周知的問題是正則化問題。當鄰域數大于輸入維數時，定義每個局部鄰域的矩陣是不滿秩的。為了解決這個問題，標準LLE應用了一個任意的正則化參數，它的取值受局部權重矩陣的跡的影響。雖然可以形式化的表示為：當正則化參數 ,解收斂于期望的嵌入,但是當時不保證找到最優解。這個問題表現在嵌入過程中扭曲了流形的基本幾何形狀。

解決正則化問題的一種方法是在每個鄰域中使用多個權重向量。這就是改進的局部線性嵌入(MLLE)算法的本質。MLLE可以通過函數 locally_linear_embedding 或者其面向對象的副本 LocallyLinearEmbedding 來執行，附帶關鍵詞 method = 'modified' 。它需要滿足 n_neighbors > n_components。

2.2.4.1. 復雜度

MLLE 算法分為三個階段:

**近鄰搜索.**與標準 LLE 的相同。
**權重矩陣構造.**大約是。該式第一項恰好等于標準 LLE 算法的復雜度。第二項與由多個權重來構造權重矩陣相關。在實踐中，構造 MLLE 權重矩陣所增加的損耗（就復雜度而言），比其它兩部分要小。
**部分特征值分解.**與標準 LLE 的相同。

綜上，MLLE 的復雜度為。

: 訓練集數據點的個數
: 輸入維度
: 最近鄰域的個數
: 輸出維度

參考資料:

“MLLE: Modified Locally Linear Embedding Using Multiple Weights” Zhang, Z. & Wang, J.

2.2.5. 黑塞特征映射（HE）

黑塞特征映射 (也稱作基于黑塞的 LLE: HLLE ）是解決 LLE 正則化問題的另一種方法。在每個用于恢復局部線性結構的鄰域內，它會圍繞一個基于黑塞的二次型展開。雖然其它的實現表明它對數據大小進行縮放的能力較差，但是 sklearn 實現了一些算法改進，使得在輸出低維度時它的損耗可與其他 LLE 變體相媲美。HLLE 通過函數 locally_linear_embedding 或其面向對象的形式 LocallyLinearEmbedding 被執行，附帶關鍵詞 method = 'hessian' 。它需滿足 n_neighbors > n_components * (n_components + 3) / 2 。

2.2.5.1. 復雜度

HLLE 算法分為三個階段:

**近鄰搜索.**與標準 LLE 的相同。
**權重矩陣構造.**大約是。其中第一項與標準LLE相似。第二項來自于局部黑塞估計量的一個 QR 分解。
**部分特征值分解.**與標準 LLE 的相同。

綜上，HLLE 的復雜度為。

: 訓練集數據點的個數
: 輸入維度
: 最近鄰域的個數
: 輸出維度

參考資料:

“Hessian Eigenmaps: Locally linear embedding techniques for high-dimensional data” Donoho, D. & Grimes, C. Proc Natl Acad Sci USA. 100:5591 (2003)

2.2.6. 譜嵌入

譜嵌入是計算非線性嵌入的一種方法。Scikit-learn實現了拉普拉斯特征映射，它使用拉普拉斯圖的譜分解方法來進行數據的低維表示。所生成的圖可以看作是低維流形在高維空間中的離散近似值。基于圖的代價函數的最小化確保流形上相互接近的點在低維空間中相互映射并保持局部距離。譜嵌入可使用行為函數 spectral_embedding 或它的面向對象的對應形式 SpectralEmbedding 來執行。

2.2.6.1. 復雜度

譜嵌入（拉普拉斯特征映射）算法包含三部分：

**加權圖結構.**把原始輸入數據轉換為用相似（鄰接）矩陣表達的圖表達。
**圖拉普拉斯結構.**非規格化的圖拉普拉斯是按構造，并按規格化。
**部分特征值分解.**在圖拉普拉斯上進行特征值分解。

綜上，譜嵌入的復雜度為。

: 訓練集數據點的個數
: 輸入維度
: 最近鄰域的個數
: 輸出維度

參考資料:

“Laplacian Eigenmaps for Dimensionality Reduction and Data Representation” M. Belkin, P. Niyogi, Neural Computation, June 2003; 15 (6):1373-1396

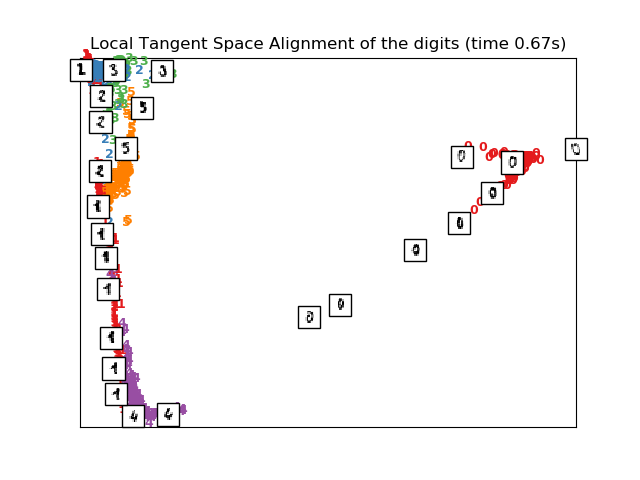
2.2.7. 局部切空間對齊（LTSA）

雖然從技術上講局部切空間對齊(LTSA) 不是LLE的變體，但在算法上與LLE非常相似，因此可以將其歸入這一類。與LLE不同的是，LTSA不像LLE那樣注重保持鄰域距離，而是通過其切空間來描述每個鄰域的局部幾何形狀，并執行全局最優化來對齊這些局部切空間以得到對應的嵌入。 LTSA 可通過函數 locally_linear_embedding 或其面向對象的對應函數 LocallyLinearEmbedding 來執行，附帶關鍵詞 method = 'ltsa' 。

2.2.7.1 復雜度

LSTA算法包含三部分：

**近鄰搜索.**與標準 LLE 的相同。
**權重矩陣構造.**大約是。其中第一項與標準LLE相似。
**部分特征值分解.**與標準 LLE 相同。

綜上，復雜度為。

: 訓練集數據點的個數
: 輸入維度
: 最近鄰域的個數
: 輸出維度

參考資料:

“Principal manifolds and nonlinear dimensionality reduction via tangent space alignment” Zhang, Z. & Zha, H. Journal of Shanghai Univ. 8:406 (2004)

2.2.8. 多維尺度分析（MDS）

多維尺度分析 Multidimensional scaling （ MDS ）尋求數據的低維表示，而且低維數據間的距離保持了它們在原始高維空間中的距離。

通常，MDS是一種用于分析相似或不同數據的技術。它試圖在幾何空間上將相似或不相似的數據進行建模。數據可以是對象之間的相似性評級，分子的相互作用頻率，或國家之間的貿易指數。

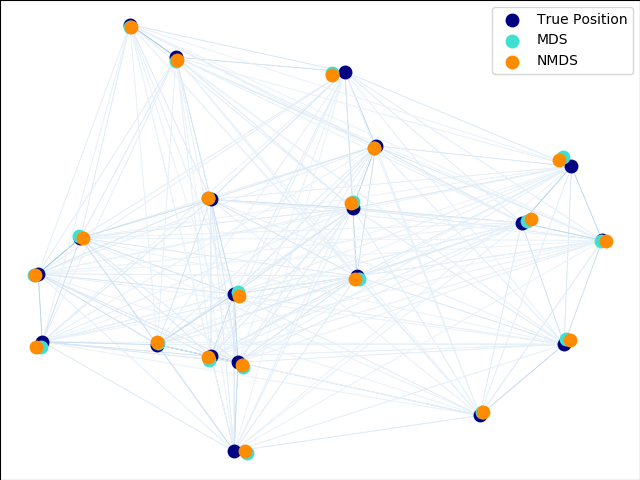
MDS算法有度量算法和非度量算法兩種。在scikit-learn中， MDS 類可以實現這兩種算法。在度量MDS中，輸入相似度矩陣源于一個度量(因此尊重三角不等式)，后設置輸出兩點之間的距離盡可能接近相似或不相似的數據。在非度量的情況下，算法會盡量保持對距離的控制，從而在嵌入空間的距離與相似點/不相似點之間尋找單調關系。

設是相似度矩陣，是個輸入點的坐標。差異是某些最優方式所選擇的相似度轉換。然后，通過 $\sum_{i

2.2.8.1. 度量 MDS

最簡單的度量 MDS 模型稱為 absolute MDS（絕對MDS），差異由定義。對于絕對 MDS，值應精確地對應于嵌入點的點和之間的距離。

大多數情況下，差異應設置為。

2.2.8.2. 非度量 MDS

非度量 MDS 關注數據的排序。如果$S_{i j}

這個問題的 a trivial solution（一個平凡解）是把所有點設置到原點上。為了避免這種情況，將差異正則化。

參考資料:

“Modern Multidimensional Scaling - Theory and Applications” Borg, I.; Groenen P. Springer Series in Statistics (1997)
“Nonmetric multidimensional scaling: a numerical method” Kruskal, J. Psychometrika, 29 (1964)
“Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis” Kruskal, J. Psychometrika, 29, (1964)

2.2.9. t 分布隨機鄰域嵌入（t-SNE）

t-SNE（ TSNE ）將數據點的相似性轉換為概率。原始空間中的相似性用高斯聯合概率表示，嵌入空間中的相似性用”學生“的t分布表示。這使得t-SNE對局部結構特別敏感，并且比現有技術有一些其他的優勢:

在一個單一映射上按多種比例顯示結構
顯示位于多個、不同的流形或聚類中的數據
減輕在中心聚集的傾向

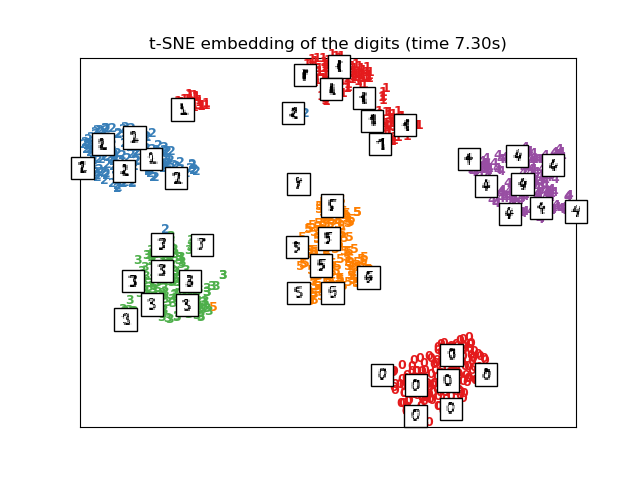
雖然Isomap、LLE和其他變體最適合展開單個連續的低維流形，但t-SNE將重點關注數據的局部結構，并傾向于提取聚類的局部樣本組，如S-curve示例中突出顯示的那樣。這種基于局部結構對樣本進行分組的能力可能有助于從視覺上分離同時包含多個流形的數據集，就像數字數據集中的情況一樣。

利用梯度下降的方法，使原始空間和嵌入空間的聯合概率的離散度達到最小。注意KL散度不是凸的，也就是說，用不同的初始化方法多次重新啟動，最終會得到KL散度的局部極小值。因此，有時嘗試不同的種子并選擇KL散度最低的KL散度的嵌入是有用的。

使用 t - SNE 的缺點大致如下:

t-SNE 的計算成本很高，在百萬樣本數據集上花費數小時，而PCA在幾秒鐘或幾分鐘內就可以完成。
Barnes-Hut t-SNE 方法僅限于二維或三維嵌入。
該算法是隨機的，不同種子的多次重啟可以產生不同的嵌入。然而，以最小的誤差選擇嵌入是完全合理的。
未明確保留全局結構。這個問題可以通過使用PCA初始化點(使用 init=’pca’)來緩解。

2.2.9.1. 優化t-SNE

t-SNE的主要目的是實現高維數據的可視化。因此，當數據被嵌入到二維或三維時，它的效果最好。

優化KL散度有時會有點棘手。有五個參數控制t-SNE的優化，因此可能也會影響最終嵌入的質量:

困惑度
早期增長因子
學習率
最大迭代次數
角度（不在精確方法中使用）

困惑度定義為，其中是條件概率分布的香農熵。面色子的復雜度是，它實際上是t-SNE在生成條件概率時考慮的最近鄰的個數。困惑度越大導致更近，對小結構也越不敏感。相反，較低的困惑度考慮的是較少的鄰域，因此忽略了更多的全局信息，而更加關注局部鄰域。隨著數據集的增大，需要更多的點來獲得合理的局部鄰域樣本，因此可能需要更大的困惑度。同樣的，噪聲越大的數據集需要越大的困惑度來包含足夠多的局部鄰居，以便在背景噪聲之外查看。

迭代的最大次數通常足夠高，不需要任何調優。優化包括兩個階段:早期增長階段和最終優化階段。在早期的增長階段，原始空間中的聯合概率將通過與給定的因子相乘而被人為地增加。越大的因子導致數據中自然聚類之間的差距越大。如果因子過高，則KL散度在此階段可能增大。通常不需要對其進行調整。一個關鍵的參數是學習率。如果梯度降得太低，就會陷入局部極小值。如果KL散度過高，則在優化過程中KL散度會增大。更多的技巧可以在Laurens van der Maaten的FAQ中找到(見參考資料)。最后一個參數角度，它是性能和精度之間的權衡。角度越大意味著我們可以用單個點來近似更大的區域，從而得到更快的速度，但結果越不準確。

“How to Use t-SNE Effectively” （如何高效使用t-SNE）提供了一個關于各種參數效果的討論，以及用來探索不同參數效果的交互式繪圖。

2.2.9.2. Barnes-Hut t-SNE

這里實現的Barnes-Hut t-SNE通常比其他流形學習算法要慢得多。優化比較困難，梯度的計算為，其中為輸出維數，為樣本數。t-SNE復雜度是,Barnes-Hut 方法在此基礎上進行了改進，但有幾個其他顯著差異:

Barnes-Hut 僅在目標維度為3或更小時才有效。構建可視化時，基于2-D的情況就是典型的用于可視化。
Barnes-Hut 僅對密集的輸入數據有效。稀疏數據矩陣只能用精確方法嵌入，或者可以通過密集的低階投影來近似，例如使用 sklearn.decomposition.TruncatedSVD
Barnes-Hut 是精確方法的近似。這個近似值是用角度參數來參數化的，因此當參數 method=”exact” 時，angle 參數無效。
Barnes-Hut 的拓展性很高。Barnes-Hut 可用于嵌入數十萬個數據點，而精確方法只能處理數千個樣本，再多就會變得難以計算。

出于可視化目的(這是t-SNE的主要用例)，強烈建議使用Barnes-Hut方法。精確的t-SNE方法可以用來檢驗高維空間中嵌入的理論性質，但由于計算能力的約束而僅限于小數據集。

還需要注意的是，數字標簽與t-SNE發現的自然聚類大致匹配，而PCA模型的線性2D投影則產生了一個標簽區域大部分重疊的表示。這是一個強有力的線索，表明該數據可以通過關注局部結構的非線性方法(例如帶有高斯RBF核的SVM)很好地分離。然而，在2維中不能很好地將t-SNE標記的均勻分組可視化并不一定意味著數據不能被監督模型正確分類。可能的情況是，2維不夠低，不能準確地表示數據的內部結構。

參考資料:

“Visualizing High-Dimensional Data Using t-SNE” van der Maaten, L.J.P.; Hinton, G. Journal of Machine Learning Research (2008)
“t-Distributed Stochastic Neighbor Embedding” van der Maaten, L.J.P.
“Accelerating t-SNE using Tree-Based Algorithms.” L.J.P. van der Maaten. Journal of Machine Learning Research 15(Oct):3221-3245, 2014.

2.2.10. 實用技巧

確保對所有特征中使用相同的縮放比例。由于流形學習方法是基于最近鄰搜索的，否則算法的性能可能很差。有關縮放異構數據的方便方法，請參閱 StandardScaler 。
每個程序計算的重構誤差可以用來選擇最優的輸出維數。對于嵌入在維參數空間中的維流形，重構誤差將隨著 n_components 的增加而減小，直到 n_components == d 。
注意，有噪聲的數據會使流形管“短路”，本質上是在流形管的各個部分之間起到橋梁作用，否則流形管就會被很好地分開。基于噪聲和/或不完全數據的流形學習是一個活躍的研究領域。
某些輸入配置可能導致奇異加權矩陣，例如，當數據集中有兩個以上的點是相同的，或者當數據被分割成不關聯的組時。在這種情況下， solver='arpack' 將無法找到零空間。解決這一問題的最簡單方法是使用 solver='dense' ，它將在一個奇異矩陣上工作，盡管它可能因為輸入點的數量而非常慢。或者，可以嘗試理解奇點的來源:如果是由于不相交的集合，增加 n_neighbors 可能會有所幫助；如果是由于數據集中的相同的點，則刪除這些點可能有所幫助。

也可以看看：完全隨機樹嵌入也可用于導出特征空間的非線性表示，并且它不執行降維。