6.3 數據預處理?
sklearn.preprocessing包提供了幾個常用的實用函數和轉換器類,用以將原始特征向量更改為更適合下游估計器的表示形式。
通常,學習算法受益于數據集的標準化。如果數據集中存在一些異常值,則更適合使用健壯的縮放器或轉換器。不同縮放器,轉換器和規范化器在包含邊緣異常值的數據集上的行為突出顯示了比較不同縮放器對含有異常值數據的效果。
6.3.1 標準化或均值去除和方差縮放
數據集的標準化是scikit-learn中實現許多機器學習估計器的普遍要求;如果個別特征看起來或多或少不像標準正態分布數據:均值和單位方差為零的高斯分布,則它們的性能可能不好。
在實踐中,我們通常會忽略分布的形狀,而只是通過刪除每個特征的平均值來實現特征數據中心化,然后除以非常數特征的標準差來縮放數據。
例如,學習算法的目標函數中使用的許多元素(例如支持向量機的RBF內核或線性模型的l1和l2正則化器)都假定所有特征都圍繞零為中心并且具有相同階數的方差。如果某個特征的方差比其他特征大幾個數量級,則它可能會極大影響目標函數,并使估計器無法按預期從其他特征中正確學習。
scale函數提供了一種簡單快捷的方法來對單個類似數組的數據集執行此操作:
>>> from sklearn import preprocessing
>>> import numpy as np
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
>>> X_scaled = preprocessing.scale(X_train)
>>> X_scaled
array([[ 0. ..., -1.22..., 1.33...],
[ 1.22..., 0. ..., -0.26...],
[-1.22..., 1.22..., -1.06...]])
縮放的數據具有0均值和單位方差:
>>> X_scaled.mean(axis=0)
array([0., 0., 0.])
>>> X_scaled.std(axis=0)
array([1., 1., 1.])
preprocessing模塊還提供了一個實用程序類StandardScaler,它使TransformerAPI來計算訓練集上的均值和標準差,以便以后能夠在測試集上重新應用相同的轉換。因此,該類適用于 sklearn.pipeline.Pipeline的早期步驟:
>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> scaler
StandardScaler()
>>> scaler.mean_
array([1. ..., 0. ..., 0.33...])
>>> scaler.scale_
array([0.81..., 0.81..., 1.24...])
>>> scaler.transform(X_train)
array([[ 0. ..., -1.22..., 1.33...],
[ 1.22..., 0. ..., -0.26...],
[-1.22..., 1.22..., -1.06...]])
然后可以將縮放器實例用于新數據以實現與訓練集相同的轉換方式:
>>> X_test = [[-1., 1., 0.]]
>>> scaler.transform(X_test)
array([[-2.44..., 1.22..., -0.26...]])
可以通過將with_mean=False或with_std=False傳遞給StandardScaler的構造函數來取消居中或縮放。
6.3.1.1 將特征縮放至特定范圍內
另一種標準化方法是將特征值縮放到給定的最小值和最大值之間,通常介于零和一之間,或者將每個特征的最大絕對值縮放到單位大小,上述操作可以分別使用MinMaxScaler或MaxAbsScaler來實現。
使用這種縮放的目的包括對特征極小標準偏差的穩健性以及在稀疏數據中保留零元素。
這是將簡單的數據矩陣縮放到[0, 1]范圍的示例:
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
...
>>> min_max_scaler = preprocessing.MinMaxScaler()
>>> X_train_minmax = min_max_scaler.fit_transform(X_train)
>>> X_train_minmax
array([[0.5 , 0. , 1. ],
[1. , 0.5 , 0.33333333],
[0. , 1. , 0. ]])
然后,相同的轉換實例可以被用與在訓練過程中不可見的測試數據:實現和訓練數據一致的縮放和移位操作:
>>> X_test = np.array([[-3., -1., 4.]])
>>> X_test_minmax = min_max_scaler.transform(X_test)
>>> X_test_minmax
array([[-1.5 , 0. , 1.66666667]])
可以檢查縮放器(scaler)屬性,以找到在訓練數據上學習到的轉換的確切性質:
>>> min_max_scaler.scale_
array([0.5 , 0.5 , 0.33...])
>>> min_max_scaler.min_
array([0. , 0.5 , 0.33...])
如果給MinMaxScaler一個明確的feature_range=(min, max),則完整公式為:
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min
MaxAbsScaler的工作方式都非常相似,通過除以每個特征中的最大值來使訓練數據位于[-1, 1]范圍內的方式進行縮放。這意味著它適用于已經以零為中心的數據或稀疏數據。
這是在此縮放器上使用上一示例中少量數據的示例:
>>> X_train = np.array([[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]])
...
>>> max_abs_scaler = preprocessing.MaxAbsScaler()
>>> X_train_maxabs = max_abs_scaler.fit_transform(X_train)
>>> X_train_maxabs
array([[ 0.5, -1. , 1. ],
[ 1. , 0. , 0. ],
[ 0. , 1. , -0.5]])
>>> X_test = np.array([[ -3., -1., 4.]])
>>> X_test_maxabs = max_abs_scaler.transform(X_test)
>>> X_test_maxabs
array([[-1.5, -1. , 2. ]])
>>> max_abs_scaler.scale_
array([2., 1., 2.])
與scale一樣,如果您不想創建對象,該模塊進一步提供了 minmax_scale和maxabs_scale函數。
6.3.1.2 縮放稀疏數據
中心化稀疏數據會破壞數據的稀疏結構,因此明智的做法是少做這樣的操作。但是,縮放稀疏輸入是有意義的,尤其是當特征處于不同的縮放比例時。
MaxAbsScaler 和maxabs_scale是專門為縮放稀疏數據而設計的,并且是實現此目的的推薦方法。然而,只要with_mean=False顯式地傳遞給構造函數,scale和StandardScaler可以接受scipy.sparse 的矩陣作為輸入。否則,將引發ValueError,因為靜默居中會破壞稀疏性,并經常由于無意中分配過多的內存而使執行崩潰。 RobustScaler不能適合稀疏輸入,但是可以在稀疏輸入上使用transform方法。
請注意,縮放器接受壓縮的稀疏行和壓縮的稀疏列格式(請參閱scipy.sparse.csr_matrix和 scipy.sparse.csc_matrix)。任何其他稀疏輸入都將轉換為“壓縮稀疏行”表示形式。為避免不必要的內存副本,建議在初期選擇CSR或CSC表示形式。
最后,如果已經中心化的數據足夠小,則使用稀疏矩陣的toarray方法將輸入的數據顯式轉換為數組是另一種選擇。
6.3.1.3 縮放包含離群值的數據
如果數據中包含許多離群值,使用數據的均值和方差進行縮放可能效果不佳。在這種情況下,可以使用 robust_scale和RobustScaler作為替代產品。他們對數據的中心和范圍的估計更可靠。
參考文獻:
常見問題解答中提供了有關對數據進行居中和縮放的重要性的進一步討論:是否應該對數據進行標準化/標準化/縮放
Scaling vs Whitening
有時候獨立地中心化和縮放數據是不夠的,因為下游模型可以進一步對特征間的線性獨立性做出一些假設。
要解決此問題,您可以使用
sklearn.decomposition.PCA并指定參數whiten=True以進一步消除特征間的線性相關性。縮放一維數組
所有上述功能(即
scale,minmax_scale,和robust_scale)都接受一維數組,這在某些特定的情況下很有用。
6.3.1.4 核矩陣的中心化
如果您擁有一個內核 的內核矩陣,可以在函數定義的特征空間中計算點積,[`KernelCenterer`](http://www.ipahlj.com/view/724.html)類可以轉換該內核矩陣使其包含由函數 定義的特征空間中的內部乘積,然后刪除該空間中的均值。
6.3.2 非線性轉換
有兩種類型的轉換是可行的:分位數轉換和冪轉換。分位數和冪變換都基于特征的單調變換,從而保持了每個特征值的秩。
分位數變換基于公式 將所有特征置于相同的期望分布中,其中 是特征的累積分布函數,并且 是期望輸出分布的 分位數函數。該公式使用了以下兩個事實:(i)如果 是具有連續累積分布函數 的隨機變量,則 均勻分布在上; (ii)如果 是在 上符合均勻分布的一個隨機變量,則 有分布。通過執行秩變換,分位數變換可以平滑不尋常的分布,并且與縮放方法相比,離群值的影響較小。但是,它確實扭曲了特征之間的相關性和距離。
冪變換是一組參數變換,旨在將數據從任何分布映射到接近高斯分布。
6.3.2.1 映射到均勻分布
QuantileTransformer和quantile_transform提供了一種非參數轉換,以將數據映射到值介于0和1之間的均勻分布:
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
>>> quantile_transformer = preprocessing.QuantileTransformer(random_state=0)
>>> X_train_trans = quantile_transformer.fit_transform(X_train)
>>> X_test_trans = quantile_transformer.transform(X_test)
>>> np.percentile(X_train[:, 0], [0, 25, 50, 75, 100])
array([ 4.3, 5.1, 5.8, 6.5, 7.9])
此特征對應以厘米為單位的花萼長度。一旦應用了分位數轉換,這些界標便會接近先前定義的百分位數:
>>> np.percentile(X_train_trans[:, 0], [0, 25, 50, 75, 100])
...
array([ 0.00... , 0.24..., 0.49..., 0.73..., 0.99... ])
可以在帶有類似注釋的獨立測試集上對此進行確認:
>>> np.percentile(X_test[:, 0], [0, 25, 50, 75, 100])
...
array([ 4.4 , 5.125, 5.75 , 6.175, 7.3 ])
>>> np.percentile(X_test_trans[:, 0], [0, 25, 50, 75, 100])
...
array([ 0.01..., 0.25..., 0.46..., 0.60... , 0.94...])
6.3.2.2 映射到高斯分布
在許多建模場景中,需要對數據集中特征進行正態化。冪變換是一組參數化的單調變換,旨在將數據從任何分布映射到盡可能接近高斯分布,以穩定方差并最小化偏度。
PowerTransformer 目前提供兩種這樣的冪變換,即Yeo-Johnson變換和Box-Cox變換。
以下為Yeo-Johnson 變換:
以下為Box-Cox變換:
Box-Cox僅可應用于嚴格的正數據。在這兩種方法中,變換都是通過最大似然估計確定的的參數化。這是使用Box-Cox將從服從對數正態分布的樣本映射到正態分布的示例:
>>> pt = preprocessing.PowerTransformer(method='box-cox', standardize=False)
>>> X_lognormal = np.random.RandomState(616).lognormal(size=(3, 3))
>>> X_lognormal
array([[1.28..., 1.18..., 0.84...],
[0.94..., 1.60..., 0.38...],
[1.35..., 0.21..., 1.09...]])
>>> pt.fit_transform(X_lognormal)
array([[ 0.49..., 0.17..., -0.15...],
[-0.05..., 0.58..., -0.57...],
[ 0.69..., -0.84..., 0.10...]])
雖然以上示例將standardize參數設置為False,但 PowerTransformer默認將零均值,單位方差歸一化應用于轉換后的輸出。
以下是適用于各種概率分布的Box-Cox和Yeo-Johnson的示例。請注意,將冪變換應用于某些分布時,會獲得非常類似于高斯的結果,但是對于其他一些分布,結果是無效的。這突出了在轉換之前和之后可視化數據的重要性。
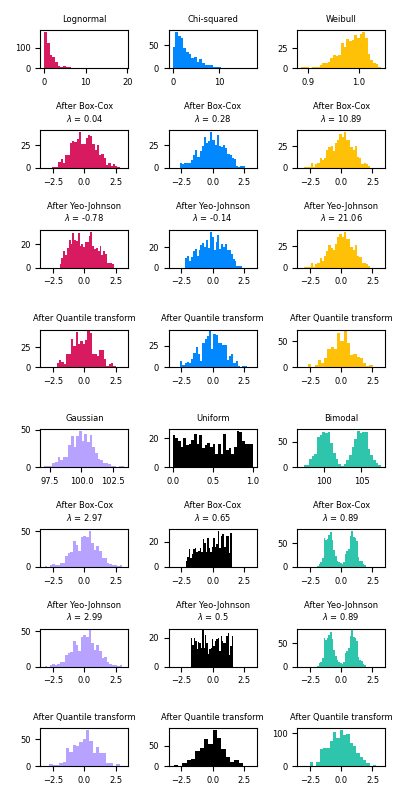
QuantileTransformer通過設置 output_distribution='normal'也可以將數據映射到正態分布。將先前的示例與iris數據集結合使用:
>>> quantile_transformer = preprocessing.QuantileTransformer(
... output_distribution='normal', random_state=0)
>>> X_trans = quantile_transformer.fit_transform(X)
>>> quantile_transformer.quantiles_
array([[4.3, 2. , 1. , 0.1],
[4.4, 2.2, 1.1, 0.1],
[4.4, 2.2, 1.2, 0.1],
...,
[7.7, 4.1, 6.7, 2.5],
[7.7, 4.2, 6.7, 2.5],
[7.9, 4.4, 6.9, 2.5]])
因此,輸入的中位數變為以0為中心輸出的平均值。正常輸出被裁剪,以便輸入的最小和最大值(分別對應于1e-7和1-1e-7分位數)在轉換后不會變成無窮。
6.3.3 歸一化
歸一化是將縮放單個樣本至單位范數的過程。如果計劃使用點積或任何其他核的二次形式來量化任何一對樣本的相似性,則此過程可能會很有用。
該假設是向量空間模型的基礎,該向量空間模型經常用于文本分類和內容聚類中。
函數normalize提供了一種快速簡便的方法,可以使用l1或l2范式在單個類似于數組的數據集上執行此操作:
>>> X = [[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]]
>>> X_normalized = preprocessing.normalize(X, norm='l2')
>>> X_normalized
array([[ 0.40..., -0.40..., 0.81...],
[ 1. ..., 0. ..., 0. ...],
[ 0. ..., 0.70..., -0.70...]])
preprocessing模塊還提供了一個實用程序類Normalizer,它使用TransformerAPI 來實現相同的操作 (即使在這種情況下fit方法無用:該類是無狀態的,因為此操作獨立地處理樣本)。
因此,該類適用于 sklearn.pipeline.Pipeline的前期步驟:
>>> normalizer = preprocessing.Normalizer().fit(X) # fit does nothing
>>> normalizer
Normalizer()
然后,可以將normalizer實例用作任何轉換器的樣本矢量:
>>> normalizer.transform(X)
array([[ 0.40..., -0.40..., 0.81...],
[ 1. ..., 0. ..., 0. ...],
[ 0. ..., 0.70..., -0.70...]])
>>> normalizer.transform([[-1., 1., 0.]])
array([[-0.70..., 0.70..., 0. ...]])
注意:L2歸一化也稱為空間符號預處理。
稀疏輸入
normalize和Normalizer都接受來自scipy.sparse的密集數組式數據和稀疏矩陣作為輸入。對于稀疏輸入,在將數據饋入有效的Cython例程之前,將數據轉換為“壓縮的稀疏行”表示形式(請參閱
scipy.sparse.csr_matrix參考資料)。為避免不必要的內存復制,建議選擇上游的CSR表示形式。
6.3.4 類別特征編碼
通常,特征不是連續值,而是分類值。例如,一個人可能具備以下特征,["male", "female"]``["from Europe", "from US", "from Asia"]``["uses Firefox", "uses Chrome", "uses Safari", "uses Internet Explorer"]。這樣的特征可以有效地編碼為整數,例如 ["male", "from US", "uses Internet Explorer"] 可以表示為[0, 1, 3] ,而["female", "from Asia", "uses Chrome"]表示為[1, 2, 1]。
要將分類特征轉換為這樣的整數代碼,我們可以使用 OrdinalEncoder。此估計器將每個分類特征轉換為一個新的整數特征(0到n_categories-1):
>>> enc = preprocessing.OrdinalEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OrdinalEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari']])
array([[0., 1., 1.]])
但是,此類整數表示不能直接在所有的scikit-learn估計器使用,因為這樣連續型數值的輸入,估計器會將類別解釋為有序的,而通常是無序的(例如,瀏覽器的類別數據是任意無序的)。
將分類特征轉換為可與scikit-learn估計器一起使用的特征的另一種方法是使用one-of-K,也稱為獨熱或偽編碼。這種類型的編碼可以通過OneHotEncoder來獲得,它將具有n_categories個可能值的每個分類特征轉換為n_categories個二進制特征,其中一個位置為1,所有其他位置為0。
繼續上面的示例:
>>> enc = preprocessing.OneHotEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari'],
... ['male', 'from Europe', 'uses Safari']]).toarray()
array([[1., 0., 0., 1., 0., 1.],
[0., 1., 1., 0., 0., 1.]])
默認情況下,每個特征可以采用的值是從數據集中自動推斷出來的,并且可以在categories_屬性中找到:
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]
可以使用參數categories顯式的指定,我們的數據集中有兩種性別,四個可能的大陸和四個Web瀏覽器:
>>> genders = ['female', 'male']
>>> locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
>>> browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
>>> enc = preprocessing.OneHotEncoder(categories=[genders, locations, browsers])
>>> # Note that for there are missing categorical values for the 2nd and 3rd
>>> # feature
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(categories=[['female', 'male'],
['from Africa', 'from Asia', 'from Europe',
'from US'],
['uses Chrome', 'uses Firefox', 'uses IE',
'uses Safari']])
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 1., 0., 0., 1., 0., 0., 0.]])
如果訓練數據有可能缺少分類特征,則通常最好指定handle_unknown='ignore'而不是如上所述手動設置categories。如果指定 handle_unknown='ignore'且在轉換過程中遇到未知類別,則不會引發任何錯誤,但此功能生成的一鍵編碼列將全為零(handle_unknown='ignore'僅支持一鍵編碼):
>>> enc = preprocessing.OneHotEncoder(handle_unknown='ignore')
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(handle_unknown='ignore')
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 0., 0., 0.]])
也可以通過使用 drop參數將每一列編碼為n_categories - 1列而不是n_categories列。該參數允許用戶為每個要刪除的特征指定一個類別。在某些分類器中,這有助于避免輸入的矩陣存在共線性。例如,當使用非正則回歸(LinearRegression)時,此類功能很有用,因為共線性會導致協方差矩陣不可逆。當此參數不為None時,必須設置handle_unknown為 :error
>>> X = [['male', 'from US', 'uses Safari'],
... ['female', 'from Europe', 'uses Firefox']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='first').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 1., 1.],
[0., 0., 0.]])
有時可能只想刪除具有2個類別特征的兩列之一。在這種情況下,可以設置參數drop='if_binary'。
>>> X = [['male', 'US', 'Safari'],
... ['female', 'Europe', 'Firefox'],
... ['female', 'Asia', 'Chrome']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='if_binary').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['Asia', 'Europe', 'US'], dtype=object), array(['Chrome', 'Firefox', 'Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 0., 0., 1., 0., 0., 1.],
[0., 0., 1., 0., 0., 1., 0.],
[0., 1., 0., 0., 1., 0., 0.]])
在轉換后的X中,第一列是類別為“ male” /“ female”的特征編碼,而其余六列則是分別具有3個類別2個特征的編碼。
請參閱從字典中加載特征以獲取表示為字典而不是標量的分類特征。
6.3.5 離散化
離散化 (也稱為量化或分箱)提供了一種將連續特征劃分為離散值的方法。某些具有連續特征的數據集可能會從離散化中受益,因為離散化可以將連續屬性的數據集轉換為僅具有名義屬性的數據集。
One-hot編碼的離散特征可以使模型更具表現力,同時保持可解釋性。例如,使用離散器的預處理可以將非線性引入線性模型。
6.3.5.1 K-bins離散化
KBinsDiscretizer將特征離散到k個容器中:
>>> X = np.array([[ -3., 5., 15 ],
... [ 0., 6., 14 ],
... [ 6., 3., 11 ]])
>>> est = preprocessing.KBinsDiscretizer(n_bins=[3, 2, 2], encode='ordinal').fit(X)
默認情況下,輸出是one-hot編碼成的稀疏矩陣(請參閱編碼分類特征),并且可以使用encode參數進行配置。對于每個特征,在箱體的邊緣和箱體數量是在fit過程中計算出來的,它們將定義區間。因此,對于當前示例,這些區間定義為:
特征1:
特征2:
特征3:
根據這些bin區間,
X轉換如下:>>> est.transform(X)
array([[ 0., 1., 1.],
[ 1., 1., 1.],
[ 2., 0., 0.]])
結果數據集包含可以在sklearn.pipeline.Pipeline進一步使用的序數屬性。
離散化類似于構造連續數據的直方圖。但是,直方圖著重于對落入特定區域的特征進行計數,而離散化則著重于為這些區域分配特征值。
KBinsDiscretizer可以通過strategy參數選擇實現不同的分箱策略。“uniform”策略使用固定寬度的箱體。“quantile”策略使用分位數值在每個特征中具有均等填充的bin。“ kmeans”策略基于對每個特征執行獨立的k均值聚類過程來定義箱體。
例子:
6.3.5.2 特征二值化
特征二值化是將數字特征用閾值過濾以獲得布爾值的過程。這對于下游概率估計器很有用,這些估計器假設輸入數據是根據多元Bernoulli分布進行分布的。例如sklearn.neural_network.BernoulliRBM這個例子。
即使歸一化計數(又稱術語頻率)或TF-IDF值的特征通常在實踐中表現得稍好一些,在文本處理過程中常常使用二進制特征值(可能是為了簡化概率推理)。
至于Normalizer,實用程序類 Binarizer在 sklearn.pipeline.Pipeline的前期步驟中使用。由于每個樣本都獨立于其他樣本進行處理,因此fit方法無濟于事:
>>> X = [[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]]
>>> binarizer = preprocessing.Binarizer().fit(X) # fit does nothing
>>> binarizer
Binarizer()
>>> binarizer.transform(X)
array([[1., 0., 1.],
[1., 0., 0.],
[0., 1., 0.]])
可以調整二值化器的閾值:
>>> binarizer = preprocessing.Binarizer(threshold=1.1)
>>> binarizer.transform(X)
array([[0., 0., 1.],
[1., 0., 0.],
[0., 0., 0.]])
對于StandardScaler和Normalizer類,預處理模塊提供了一個伴隨函數binarize ,以便在不需要轉換器API時使用。
請注意,當k = 2且bin邊緣處于該閾值threshold時,Binarizer與KBinsDiscretizer 類似。
稀疏輸入
binarize和Binarizer接受來自scipy.sparse的密集數組數據和稀疏矩陣作為輸入。對于稀疏輸入,數據將轉換為“壓縮的稀疏行”表示形式(請參見參考資料
scipy.sparse.csr_matrix)。為避免不必要的內存復制,建議選擇上游的CSR表示形式。
6.3.6. 估算缺失值
6.3.7 生成多項式特征
通常,考慮輸入數據的非線性特征會增加模型的復雜性。多項式特征是一種簡單而常用的方法,它可以獲取特征的高階和相互作用項。它在PolynomialFeatures中實現:
>>> import numpy as np
>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
[2, 3],
[4, 5]])
>>> poly = PolynomialFeatures(2)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.]])
特征已經從轉換成。
在某些情況下,僅需要特征之間的交互項,并且可以通過設置interaction_only=True獲得:
>>> X = np.arange(9).reshape(3, 3)
>>> X
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> poly = PolynomialFeatures(degree=3, interaction_only=True)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 2., 0., 0., 2., 0.],
[ 1., 3., 4., 5., 12., 15., 20., 60.],
[ 1., 6., 7., 8., 42., 48., 56., 336.]])
X的特征已從 轉換成。
請注意,使用多項式內核函數時,多項式特征在 kernel methods 中被隱含調用(例如sklearn.svm.SVC,sklearn.decomposition.KernelPCA)。
有關使用創建的多項式特征的Ridge回歸的信息,請參見多項式插值。
6.3.8 自定義轉換器
通常,需要將現有的Python函數轉換為轉換器,以幫助進行數據清理或處理。可以使用FunctionTransformer將任意函數轉化成轉換器。例如,要構建在管道中應用對數轉換的轉換器,請執行以下操作:
>>> import numpy as np
>>> from sklearn.preprocessing import FunctionTransformer
>>> transformer = FunctionTransformer(np.log1p, validate=True)
>>> X = np.array([[0, 1], [2, 3]])
>>> transformer.transform(X)
array([[0. , 0.69314718],
[1.09861229, 1.38629436]])
在進行轉換之前需要通過設置check_inverse=True和調用fit來確保func和inverse_func是彼此的逆。請注意,一個警告會被拋出,并且可以通過一個 filterwarnings將其轉化為錯誤。
>>> import warnings
>>> warnings.filterwarnings("error", message=".*check_inverse*.",
... category=UserWarning, append=False)
有關演示如何使用FunctionTransformer 進行自定義特征選擇的完整代碼示例,請參見使用FunctionTransformer選擇列
