sklearn.linear_model.LinearRegression?
class sklearn.linear_model.LinearRegression(*, fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
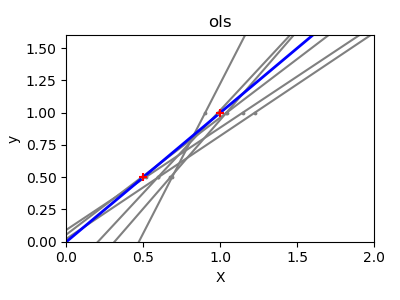
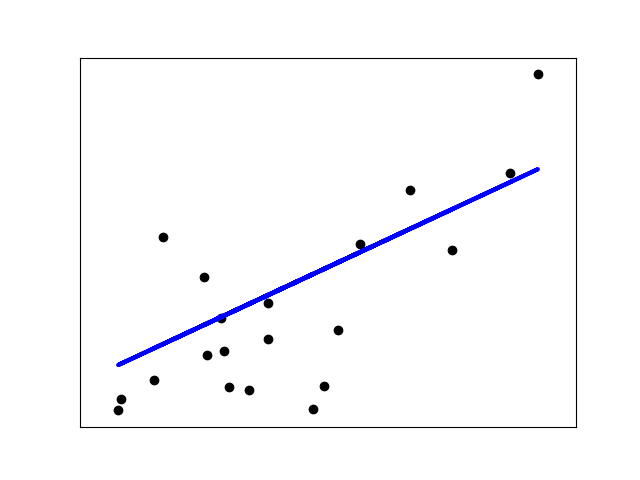
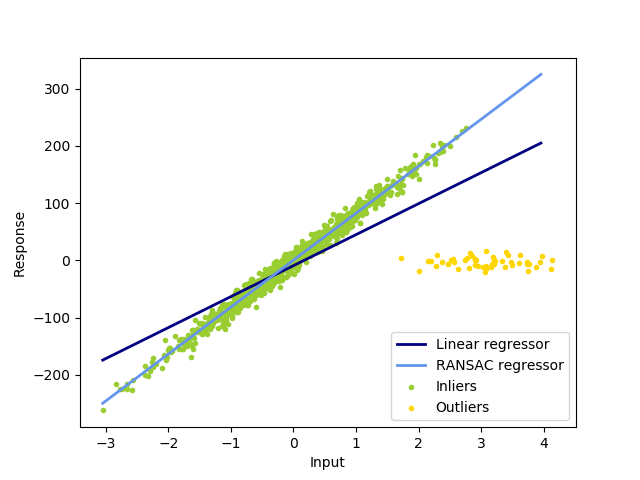
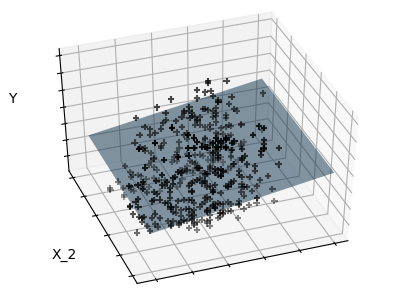
普通最小二乘線性回歸。
LinearRegression使用系數w =(w1,…,wp)擬合線性模型,以最小化數據集中實際目標值與通過線性逼近預測的目標之間的殘差平方和。
| 參數 | 說明 |
|---|---|
| fit_intercept | bool, default=True 是否計算此模型的截距。如果設置為False,則在計算中將不使用截距(即,數據應中心化)。 |
| normalize | bool, default=Falsefit_intercept設置為False 時,將忽略此參數。如果為True,則在回歸之前通過減去均值并除以l2-范數來對回歸變量X進行歸一化。如果你希望標準化,請先使用 sklearn.preprocessing.StandardScaler,然后調用fit 估算器并設置normalize=False。 |
| copy_X | bool, default=True 如果為True,將復制X;否則X可能會被覆蓋。 |
| n_jobs | int, default=None 用于計算的核心數。這只會為n_targets> 1和足夠大的問題提供加速。 除非在上下文中設置了 joblib.parallel_backend參數,否則None表示1 。 -1表示使用所有處理器。更多詳細信息,請參見詞匯表。 |
| 屬性 | 說明 |
|---|---|
| coef_ | array of shape (n_features, ) or (n_targets, n_features) 線性回歸問題的估計系數。如果在擬合過程中傳遞了多個目標(y 2D),則這是一個二維數組,形狀為(n_targets, n_features),而如果僅傳遞了一個目標,則是長度為n_features的一維數組。 |
| rank_ | int 矩陣 X的秩。僅在X是密集矩陣時可用。 |
| singular_ | array of shape (min(X, y),)X的奇異值。僅在X是密集矩陣時可用。 |
| intercept_ | float or array of shape (n_targets,) 線性模型中的截距項。如果設置 fit_intercept = False,則截距為0.0 。 |
另見
Ridge回歸通過使用L2正則化對系數的大小進行懲罰來解決普通最小二乘的一些問題。
Lasso是一個線性模型,它使用L1正則化來估計稀疏系數。
sklearn.linear_model.ElasticNetElastic-Net是使用系數的L1和L2-范數正則化訓練的線性回歸模型。
注
從實現的角度來看,這只是包裝為預測對象的普通最小二乘(scipy.linalg.lstsq)。
示例
>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression
>>> X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
>>> # y = 1 * x_0 + 2 * x_1 + 3
>>> y = np.dot(X, np.array([1, 2])) + 3
>>> reg = LinearRegression().fit(X, y)
>>> reg.score(X, y)
1.0
>>> reg.coef_
array([1., 2.])
>>> reg.intercept_
3.0000...
>>> reg.predict(np.array([[3, 5]]))
array([16.])
方法
| 方法 | 說明 |
|---|---|
fit(self, X, y[, sample_weight]) |
擬合線性模型。 |
get_params(self[, deep]) |
獲取此估計器的參數。 |
predict(self, X) |
使用線性模型進行預測。 |
score(self, X, y[, sample_weight]) |
返回預測的確定系數R ^ 2。 |
set_params(self, **params) |
設置此估計器的參數。 |
__init__(self, *, fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
初始化self, 請參閱help(type(self))以獲得準確的說明。
fit(self,X,y,sample_weight = None )
[源碼]
擬合線性模型。
| 參數 | 說明 |
|---|---|
| X | {ndarray, sparse matrix} of shape (n_samples, n_features) 訓練數據 |
| y | array-like of shape (n_samples,) or (n_samples, n_targets) 目標標簽。如有必要,將強制轉換為X的類型。 |
| sample_weight | array-like of shape (n_samples,), default=None 每個樣本的權重 *0.17版中的新功能:sample_weight參數支持LinearRegression。 |
| 返回值 | 說明 |
|---|---|
| self | returns an instance of self. 返回估計器的實例。 |
get_params(self,deep = True )
[源碼]
獲取此估計器的參數。
| 參數 | 說明 |
|---|---|
| deep | bool, default=True 如果為True,返回此估計器和所包含子對象的參數。 |
| 返回值 | 說明 |
|---|---|
| params | mapping of string to any 參數名稱映射到其值。 |
predict(self, X)
[源碼]
使用線性模型進行預測。
| 參數 | 說明 |
|---|---|
| X | array_like or sparse matrix, shape (n_samples, n_features) 樣本數據 |
| 返回值 | 說明 |
|---|---|
| C | array, shape [n_samples] 返回預測值。 |
score(self,X,y,sample_weight = None )
[源碼]
返回預測的確定系數R ^ 2。
系數R ^ 2定義為(1- u / v),其中u是殘差平方和((y_true-y_pred)** 2).sum(),而v是總平方和((y_true- y_true.mean())** 2).sum()。可能的最高得分為1.0,并且也可能為負(因為該模型可能會更差)。一個常數模型總是預測y的期望值,而不考慮輸入特征,得到的R^2得分為0.0。
| 參數 | 說明 |
|---|---|
| X | array-like of shape (n_samples, n_features) 測試樣本。對于某些估計量,這可以是預先計算的內核矩陣或通用對象列表,形狀為(n_samples,n_samples_fitted),其中n_samples_fitted是用于擬合估計器的樣本數。 |
| y | array-like of shape (n_samples,) or (n_samples, n_outputs) X的真實值。 |
| sample_weight | array-like of shape (n_samples,), default=None 樣本權重。 |
| 返回值 | 說明 |
|---|---|
| score | float 預測值與真實值的R^2。 |
注
調用回歸器中的score時使用的R2分數,multioutput='uniform_average'從0.23版開始使用 ,與r2_score默認值保持一致。這會影響多輸出回歸的score方法( MultiOutputRegressor除外)。
set_params(self, **params)
[源碼]
設置此估算器的參數。
該方法適用于簡單的估計器以及嵌套對象(例如管道)。后者具有形式為 <component>__<parameter>的參數,這樣就可以更新嵌套對象的每個組件。
| 參數 | 說明 |
|---|---|
| **params | dict 估計器參數。 |
| 返回值 | 說明 |
|---|---|
| self | object 估計器實例。 |